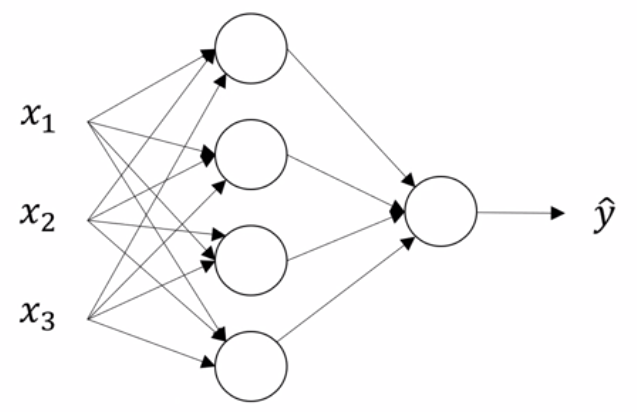
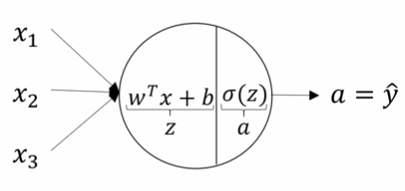
下面是一个只有一个隐层的神经网络,本文的所有工作将基于该网络,同过最简单的神经网络去理解前向传播,计算向量化,激活函数,基于链式法则的反向传播算法。
1 前向传播计算
1.1 前向传播表示
为了方便,我们首先给该网络的每一个元素用数学符号表示。如下图
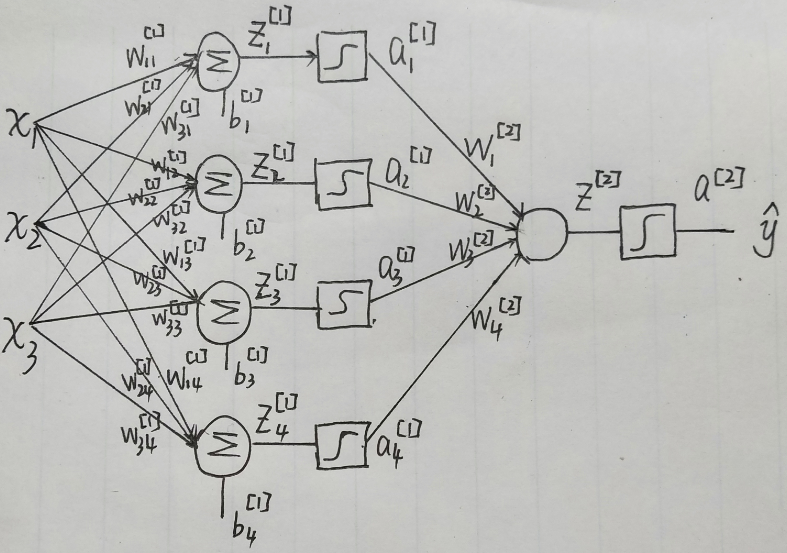
{z1[1]=w11[1]x1+w21[1]x2+w31[1]x3+b1[1]z2[1]=w12[1]x1+w22[1]x2+w32[1]x3+b2[1]z3[1]=w13[1]x1+w23[1]x2+w33[1]x3+b3[1]z4[1]=w14[1]x1+w24[1]x2+w34[1]x3+b4[1] \left\{\begin{matrix} z_1^{[1]}=w_{11}^{[1]}x_1+w_{21}^{[1]}x_2+w_{31}^{[1]}x_3+b_1^{[1]}\\ z_2^{[1]}=w_{12}^{[1]}x_1+w_{22}^{[1]}x_2+w_{32}^{[1]}x_3+b_2^{[1]}\\ z_3^{[1]}=w_{13}^{[1]}x_1+w_{23}^{[1]}x_2+w_{33}^{[1]}x_3+b_3^{[1]}\\ z_4^{[1]}=w_{14}^{[1]}x_1+w_{24}^{[1]}x_2+w_{34}^{[1]}x_3+b_4^{[1]} \end{matrix}\right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧z1[1]=w11[1]x1+w21[1]x2+w31[1]x3+b1[1]z2[1]=w12[1]x1+w22[1]x2+w32[1]x3+b2[1]z3[1]=w13[1]x1+w23[1]x2+w33[1]x3+b3[1]z4[1]=w14[1]x1+w24[1]x2+w34[1]x3+b4[1]
经过隐层激活函数有
{a1[1]=σ(z1[1])a2[1]=σ(z2[1])a3[1]=σ(z3[1])a4[1]=σ(z4[1])
\left\{\begin{matrix}
a_1^{[1]}=\sigma(z_1^{[1]})\\
a_2^{[1]}=\sigma(z_2^{[1]})\\
a_3^{[1]}=\sigma(z_3^{[1]})\\
a_4^{[1]}=\sigma(z_4^{[1]})
\end{matrix}\right.
⎩⎪⎪⎪⎨⎪⎪⎪⎧a1[1]=σ(z1[1])a2[1]=σ(z2[1])a3[1]=σ(z3[1])a4[1]=σ(z4[1])
输出层求和
z[2]=w1[2]a1[1]+w2[2]a2[1]+w3[2]a3[1]+w4[2]a4[1]+b[2]z^{[2]}=w_1^{[2]}a_1^{[1]}+w_2^{[2]}a_2^{[1]}+w_3^{[2]}a_3^{[1]}+w_4^{[2]}a_4^{[1]}+b^{[2]}z[2]=w1[2]a1[1]+w2[2]a2[1]+w3[2]a3[1]+w4[2]a4[1]+b[2]
输出层激活函数有
a[2]=σ(z[2])a^{[2]}=\sigma (z^{[2]})a[2]=σ(z[2])
上式中a[2]=y^a^{[2]}=\hat{y}a[2]=y^,也就是我们的输出。
1.2 前向传播向量化
在1.1中的四个计算式可以用向量的方式来表示,则一次前向传播可用向量表示成
{z[1]=W[1]x+b[1]→4×1=(4×3)∗(3×1)+4×1a[1]=σ(z[1])→4×1=4×1z[2]=W[2]a[1]+b[2]→1=(1×4)∗(4×1)+1a[2]=σ(z[2])→1=1
\left\{\begin{aligned}
&z^{[1]}=W^{[1]}x+b^{[1]}&\rightarrow& 4\times 1 = (4 \times 3 )* (3 \times 1) + 4 \times 1\\
&a^{[1]}=\sigma(z^{[1]}) &\rightarrow& 4\times 1 = 4\times 1\\
&z^{[2]}=W^{[2]}a^{[1]}+b^{[2]} &\rightarrow& 1 = (1 \times 4)*(4\times 1)+ 1\\
&a^{[2]}=\sigma (z^{[2]}) &\rightarrow& 1 = 1
\end{aligned}\right.
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧z[1]=W[1]x+b[1]a[1]=σ(z[1])z[2]=W[2]a[1]+b[2]a[2]=σ(z[2])→→→→4×1=(4×3)∗(3×1)+4×14×1=4×11=(1×4)∗(4×1)+11=1
上面4个式子都是矩阵和向量的运算,如果需要一次计算mmm个样本,则只需要将xxx按例扩展成一个3×m3\times m3×m的矩阵,如下
{Z[1]=W[1]X+B[1]→4×m=(4×3)∗(3×m)+(4×m)A[1]=σ(Z[1])→4×m=4×mZ[2]=W[2]A[1]+B[2]→1×m=(1×4)∗(4×m)+(1×m)A[2]=σ(Z[2])→1×m=1×m
\left\{\begin{aligned}
& Z^{[1]}=W^{[1]}X+B^{[1]}&\rightarrow& 4\times m = (4 \times 3 )* (3 \times m) + (4 \times m)\\
&A^{[1]}=\sigma(Z^{[1]}) &\rightarrow& 4\times m = 4\times m\\
&Z^{[2]}=W^{[2]}A^{[1]}+B^{[2]}&\rightarrow& 1\times m = (1 \times 4)*(4\times m)+ (1\times m)\\
&A^{[2]}=\sigma (Z^{[2]}) &\rightarrow& 1\times m = 1\times m
\end{aligned}\right.
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧Z[1]=W[1]X+B[1]A[1]=σ(Z[1])Z[2]=W[2]A[1]+B[2]A[2]=σ(Z[2])→→→→4×m=(4×3)∗(3×m)+(4×m)4×m=4×m1×m=(1×4)∗(4×m)+(1×m)1×m=1×m
如上所示我们同时在箭头右边标注了该式子的维度计算变化。这里的BBB在bbb基础上横向扩展了mmm列,在编程时由于Python语言具有广播机制,所并不需要我们手动扩展,它会自动帮我们把bbb扩展成BBB。
2 激活函数
神经网络必须引入激活函数来提供模型的非线性,否则无论网络有多少层,输出只是输入的线性组合。常见的激活函数有sigmoid函数σ(x)=1/(1+e−x)\sigma(x)=1/(1+e^{-x})σ(x)=1/(1+e−x),tanh函数tanh(x)=ex−e−xex+e−xtanh(x)=\frac {e^x - e^{-x}}{e^x + e^{-x}}tanh(x)=ex+e−xex−e−x,ReLU函数ReLU(x)=max(0,x)ReLU(x)=max(0,x)ReLU(x)=max(0,x)和ReLU的变种。
三个激活函数的导数可以通过复合函数求导法则得到:
σ′(x)=∂σ∂x=σ(x)(1−σ(x))\sigma^{'}(x)=\frac {\partial \sigma}{\partial x} = \sigma(x)(1-\sigma(x))σ′(x)=∂x∂σ=σ(x)(1−σ(x))
tanh′(x)=∂tanh∂x=1−tanh2(x) tanh^{'}(x)=\frac {\partial tanh}{\partial x} = 1 - tanh^2(x)tanh′(x)=∂x∂tanh=1−tanh2(x)
在x=0x=0x=0这一点ReLU是没法求导的,我们直接可以修改定义该点导数为0或1都是可以的,则
ReLU′(x)=0, x<0ReLU′(x)=1, x≥0
\begin{matrix}
ReLU^{'}(x)=0,\ x<0\\
ReLU^{'}(x)=1,\ x\geq 0
\end{matrix}
ReLU′(x)=0, x<0ReLU′(x)=1, x≥0
激活函数的性质
1. 非线性,这是为什么引入激活函数的原因
2. 可微性,保证反向传播梯度下降时可以求导
3. 单调性,保证单层网络是凸函数,利于优化
ReLU的优点
1. 求导右侧为1,有效抑制梯度消失
2. 左侧始终为0,为网络提供了稀疏性
3. 计算简单,减小计算量
4. 不像sigmoid和tanh在数值较大时梯度很小,收敛很慢。
3 反向传播
下面我们看看怎样利用反向传播算法,来计算各部分的偏导数,请看下图

我们的任务是通过反向传播来计算dW[2]=∂L∂W[2] ,db[2]=∂L∂b[2] ,dW[1]=∂L∂W[1] ,db[1]=∂L∂b[1]dW^{[2]}=\frac {\partial L}{\partial W^{[2]}}\ ,db^{[2]} = \frac {\partial L}{\partial b^{[2]}}\ ,dW^{[1]}=\frac {\partial L}{\partial W^{[1]}}\ ,db^{[1]}=\frac {\partial L}{\partial b^{[1]}}dW[2]=∂W[2]∂L ,db[2]=∂b[2]∂L ,dW[1]=∂W[1]∂L ,db[1]=∂b[1]∂L然后通过,梯度下降法更新我们的所有参数。
{W[2]=W[2]−α dW[2]b[2]=b[2]−α db[2]W[1]=W[1]−α dW[1]b[1]=b[1]−α db[1]
\left\{\begin{aligned}
&W^{[2]} = W^{[2]} - \alpha \ dW^{[2]}\\
&b^{[2]} = b^{[2]} - \alpha \ db^{[2]}\\
&W^{[1]} = W^{[1]} - \alpha \ dW^{[1]}\\
&b^{[1]} = b^{[1]} - \alpha \ db^{[1]}
\end{aligned}\right.
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧W[2]=W[2]−α dW[2]b[2]=b[2]−α db[2]W[1]=W[1]−α dW[1]b[1]=b[1]−α db[1]
我们的损失函数采用对数损失函数
L(a[2],y)=−yloga[2]−(1−y)log(1−a[2])L(a^{[2]},y) = -yloga^{[2]} - (1-y)log(1-a^{[2]})L(a[2],y)=−yloga[2]−(1−y)log(1−a[2])
下面我们依然先用一个样本进行反向误差传播来推导,(这里推导有问题,以后再改)
{∂L∂W[2]=∂L∂a[2]∂a[2]∂z[2]∂z[2]∂W[2]=(−ya[2]+1−y1−a[2])a[2](1−a[2])a[1]=(a[2]−y)a[1]∂L∂b[2]=∂L∂a[2]∂a[2]∂z[2]∂z[2]∂b[2]=(−ya[2]+1−y1−a[2])a[2](1−a[2])=a[2]−y∂L∂W[1]=∂L∂a[2]∂a[2]∂z[2]∂z[2]∂a[1]∂a[1]∂z[1]∂z[1]∂W[1]=W[2]T(a[2]−y)a[1](1−a[1])xT∂L∂b[1]=∂L∂a[2]∂a[2]∂z[2]∂z[2]∂a[1]∂a[1]∂z[1]∂z[1]∂b[1]=W[2]T(a[2]−y)a[1](1−a[1])\left\{\begin{aligned}
&\frac {\partial L}{\partial W^{[2]}}
=\frac {\partial L}{\partial a^{[2]}}
\frac {\partial a^{[2]}}{\partial z^{[2]}}
\frac {\partial z^{[2]}}{\partial W^{[2]}}
=(-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}})a^{[2]}(1-a^{[2]})a^{[1]}=(a^{[2]}-y)a^{[1]}\\ \\
&\frac {\partial L}{\partial b^{[2]}}
=\frac {\partial L}{\partial a^{[2]}}
\frac {\partial a^{[2]}}{\partial z^{[2]}}
\frac {\partial z^{[2]}}{\partial b^{[2]}}
=(-\frac{y}{a^{[2]}}+\frac{1-y}{1-a^{[2]}})a^{[2]}(1-a^{[2]})=a^{[2]}-y \\ \\
&\frac {\partial L}{\partial W^{[1]}}
=\frac {\partial L}{\partial a^{[2]}}
\frac {\partial a^{[2]}}{\partial z^{[2]}}
\frac {\partial z^{[2]}}{\partial a^{[1]}}
\frac {\partial a^{[1]}}{\partial z^{[1]}}
\frac {\partial z^{[1]}}{\partial W^{[1]}}
=W^{[2]T}(a^{[2]}-y)a^{[1]}(1-a^{[1]})x^T\\ \\
&\frac {\partial L}{\partial b^{[1]}}
=\frac {\partial L}{\partial a^{[2]}}
\frac {\partial a^{[2]}}{\partial z^{[2]}}
\frac {\partial z^{[2]}}{\partial a^{[1]}}
\frac {\partial a^{[1]}}{\partial z^{[1]}}
\frac {\partial z^{[1]}}{\partial b^{[1]}}
=W^{[2]T}(a^{[2]}-y)a^{[1]}(1-a^{[1]})
\end{aligned}\right.⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧∂W[2]∂L=∂a[2]∂L∂z[2]∂a[2]∂W[2]∂z[2]=(−a[2]y+1−a[2]1−y)a[2](1−a[2])a[1]=(a[2]−y)a[1]∂b[2]∂L=∂a[2]∂L∂z[2]∂a[2]∂b[2]∂z[2]=(−a[2]y+1−a[2]1−y)a[2](1−a[2])=a[2]−y∂W[1]∂L=∂a[2]∂L∂z[2]∂a[2]∂a[1]∂z[2]∂z[1]∂a[1]∂W[1]∂z[1]=W[2]T(a[2]−y)a[1](1−a[1])xT∂b[1]∂L=∂a[2]∂L∂z[2]∂a[2]∂a[1]∂z[2]∂z[1]∂a[1]∂b[1]∂z[1]=W[2]T(a[2]−y)a[1](1−a[1])
上面我们写出了较详细的推导过程,为了表达和计算的方面我们可以更方便的表述为
{dz[2]=a[2]−y→1=1−1dW[2]=dz[2]a[1]T→4×1=1∗(1×4)db[2]=dz[2]→1=1dz[1]=W[2]Tdz[2]g[1]′(z[1])→4×1=(4×1)∗1.∗(4×1)dW[1]=dz[1]xT→4×3=(4×1)∗(1×3)db[1]=dz[1]→4×1=4×1
\left\{\begin{aligned}
&dz^{[2]} = a^{[2]}-y & \rightarrow & 1 = 1 - 1\\
&dW^{[2]} = dz^{[2]}a^{[1]T} & \rightarrow & 4\times 1 = 1*(1\times 4)\\
&db^{[2]} = dz^{[2]} & \rightarrow & 1 = 1\\
&dz^{[1]} = W^{[2]T}dz^{[2]}g^{[1]'}(z^{[1]}) & \rightarrow & 4\times 1 = (4\times 1)* 1 .*(4\times 1)\\
&dW^{[1]} = dz^{[1]}x^T & \rightarrow & 4\times 3 = (4\times 1)*(1\times 3)\\
&db^{[1]} = dz^{[1]} & \rightarrow & 4\times 1 =4\times 1
\end{aligned}\right.
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧dz[2]=a[2]−ydW[2]=dz[2]a[1]Tdb[2]=dz[2]dz[1]=W[2]Tdz[2]g[1]′(z[1])dW[1]=dz[1]xTdb[1]=dz[1]→→→→→→1=1−14×1=1∗(1×4)1=14×1=(4×1)∗1.∗(4×1)4×3=(4×1)∗(1×3)4×1=4×1
这里g[1]′(z[1])=a[1](1−a[1])g^{[1]'}(z^{[1]})=a^{[1]}(1-a^{[1]})g[1]′(z[1])=a[1](1−a[1])是隐层激活函数的导数。而在输出层为了化简,我们已经把输出的激活函数相对于z[2]z^{[2]}z[2]的导数做了化简处理,得到了dz[2]=∂L∂a[2]∂a[2]∂z[2]=a[2]−ydz^{[2]} = \frac {\partial L}{\partial a^{[2]}}\frac {\partial a^{[2]}}{\partial z^{[2]}} = a^{[2]}-ydz[2]=∂a[2]∂L∂z[2]∂a[2]=a[2]−y。
到此我们推导了一个样本反向误差传播,如果有mmm个样本,我们同样将xxx所有样本排成n×mn\times mn×m的矩阵,nnn为单个样本维度,mmm为样本数量。则,上面6个式子可以改成
{dZ[2]=A[2]−Y→1×m=(1×m)−(1×m)dW[2]=1mdZ[2]A[1]T→1×4=(1×m)∗(m×4)db[2]=1mnp.sum(dZ[2],axis=1,keepdims=True)→1=(1×m) add by linedZ[1]=W[2]TdZ[2]g[1]′(Z[1])→4×m=(4×1)∗(1×m).∗(4×m)dW[1]=1mdZ[1]XT→4×3=(4×m)∗(m×3)db[1]=1mnp.sum(dZ[1],axis=1,keepdims=True)→4×1=(4×m) add by line
\left\{\begin{aligned}
&dZ^{[2]} = A^{[2]}-Y & \rightarrow & 1\times m = (1\times m) - (1\times m)\\
&dW^{[2]} = \frac {1}{m}dZ^{[2]}A^{[1]T} & \rightarrow & 1\times 4 = (1\times m)*(m\times 4)\\
&db^{[2]} = \frac {1}{m}np.sum(dZ^{[2]},axis=1,keepdims=True) & \rightarrow & 1 = (1\times m) \ add\ by\ line\\
&dZ^{[1]} = W^{[2]T}dZ^{[2]}g^{[1]'}(Z^{[1]}) & \rightarrow & 4\times m = (4\times 1)*(1\times m).*(4\times m)\\
&dW^{[1]} = \frac {1}{m}dZ^{[1]}X^T & \rightarrow & 4\times 3 = (4\times m)*(m\times 3 )\\
&db^{[1]} = \frac {1}{m}np.sum(dZ^{[1]},axis=1,keepdims=True) & \rightarrow & 4\times 1 = (4\times m) \ add\ by\ line\\
\end{aligned}\right.
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧dZ[2]=A[2]−YdW[2]=m1dZ[2]A[1]Tdb[2]=m1np.sum(dZ[2],axis=1,keepdims=True)dZ[1]=W[2]TdZ[2]g[1]′(Z[1])dW[1]=m1dZ[1]XTdb[1]=m1np.sum(dZ[1],axis=1,keepdims=True)→→→→→→1×m=(1×m)−(1×m)1×4=(1×m)∗(m×4)1=(1×m) add by line4×m=(4×1)∗(1×m).∗(4×m)4×3=(4×m)∗(m×3)4×1=(4×m) add by line
4 Python代码动手实现
由于在高维没法画图,这里我们以输入为1维,输出1一维的情形( 即y^=h(x)\hat{y}=h(x)y^=h(x) ,训练一个网络对数据进行曲线拟合,并画出拟合曲线来。
4.1 手动造点数据
# 引入包
import numpy as np
import matplotlib.pyplot as plt
我们用曲线y=x2或者y=0.2(sin(4x)+1)y= x^2或者y = 0.2(sin(4x) + 1)y=x2或者y=0.2(sin(4x)+1)来制造的数据。
n = 1 # 数据维度
m = 200 # 数据条数
x0 = np.arange(-1, 1, 0.01).reshape(1, m) # 输入
y0 = 0.2 * (np.sin(4*x0) + 1) # 产生数据的模型
# y0 = x0**2
noise = 0.05 * np.random.randn(1, m) # 噪声
yn = (y0 + noise).reshape(1, m) # 加躁标签
trainset = np.r_[x0, yn].reshape(2, m) # 数据集
4.2 初始化
在初始化的时候我们需要明确几个概念
batchsize:批大小。在深度学习中,一般采用SGD训练,即每次训练在训练集中取batchsize个样本训练;
iteration:1个iteration等于使用batchsize个样本训练一次;
epoch:1个epoch等于使用训练集中的全部样本训练一次,通俗的讲epoch的值就是整个数据集被轮几次。
hidden_size = 30 # 隐层大小
W2 = np.random.rand(1, hidden_size) # 随机初始化网络参数
b2 = np.random.rand(1, 1)
W1 = np.random.rand(hidden_size, 1)
b1 = np.random.rand(hidden_size, 1)
learing_rate = 0.3 # 学习速率
iteration = 200000 # 迭代次数
batch_size = 50 # 批大小
error = np.zeros(iteration, float) # 错误率
重要参数解释
hidden_size: 隐层需要根据实际问题的复杂性来选择适合的节点数目,节点越多拟合能力越强,但是训练所花代价也相对较高。
W,b: 网络参数需要随机初始化,防止网络中隐层节点对称造成的每个节点函数一样;且一般是较小的值,防止激活函数饱和。
learning_rate:学习速率越大,则梯度下降越快,训练收敛越快,但是当学习速率过大将会导致不收敛。学习速率小,收敛慢,最终结果越精确,但是下降很慢,需要迭代次数需要增加。
iteration: 迭代次数一般越多,结果越准确,迭代次数太多则会出现过拟合。
batch_size: 1≤batch_size≤m1 \leq batch\_size \leq m1≤batch_size≤m , 批次大小影响了梯度,一般批次越大
以上几个参数的理解是神经网络中十分重要的内容,需要重视
4.3 训练
不严谨的叙述:
训练时我们使用的激活函数是sigmoid,所以在拟合的时候最好做数据归一化,把数据范围调整到[0,1],不然将会使sigmoid饱和从而训练十分慢,或者不收敛,或者内存溢出。由于开始没有注意这一点,我直接弄了个数值范围较大的函数,再怎么调也不收敛。这里我依然没有归一化,而是直接把要拟合的函数缩小到了区间内。正确的做法依然是要首先归一化数据的,这个我以后再做。
其实tanh都比sigmoid函数好,现在深度学习一般选择的激活函数是ReLU系列。
for i in range(iteration):
# 从训练集中取一批数据
index = np.random.randint(0, m-1, (1, batch_size))
x = trainset[0, index].reshape(1, batch_size)
y = trainset[1, index].reshape(1, batch_size)
# 1. 前向传播
Z1 = np.dot(W1, x) + b1
A1 = 1/(1 + np.exp(-Z1))
Z2 = np.dot(W2, A1) + b2
A2 = 1/(1 + np.exp(-Z2))
# 2. 反向传播
dZ2 = A2 - y
error[i] = np.sum(np.abs(dZ2), axis=1, keepdims=True)
dW2 = np.dot(dZ2, A1.T) / m
db2 = np.sum(dZ2, axis=1, keepdims=True) / m
W2 = W2 - learing_rate * dW2
b2 = b2 - learing_rate * db2
dZ1 = np.dot(W2.T, dZ2) * (A1*(1 - A1))
dW1 = np.dot(dZ1, x.T) / m
db1 = np.sum(dZ1, axis=1, keepdims=True) / m
W1 = W1 - learing_rate * dW1
b1 = b1 - learing_rate * db1
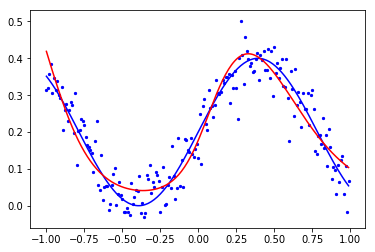
4.4 画图
# 画原始数据
plt.plot(x0.T, y0.T, c='b') # 真实数据曲线
plt.scatter(x0, yn, c='b', s=5) # 加躁数据散点图
# 网络预测
test_data = np.arange(-1, 1, 0.01).reshape(1, 200)
Z1 = np.dot(W1, test_data) + b1
A1 = 1/(1 + np.exp(-Z1))
Z2 = np.dot(W2, A1) + b2
A2 = 1/(1 + np.exp(-Z2))
# 画数预测拟合曲线
plt.plot(test_data.T, A2.T, c='r')
plt.show()
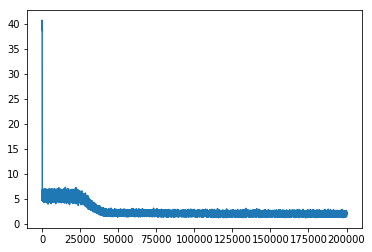
# 画出误差曲线
iter_x = np.arange(iteration)
plt.plot(iter_x, error)
plt.show()
5 手写神经网络代码总结
完全手写神经网络对于对深度学习不太熟练的人真的十分有意义。通过手写这个神经网络,我对细节的了解更加深刻,我学习到了以下几点:
1. 神经网络的前向传播
2. 神经网络损失函数的选择,为什么这里选择交叉熵,而不选择平方误差。
3. 神经网络反向传播的全部细节。包括如何运用链式求导法则进行推导,理解了误差是怎么逐级传播和修正的。
4. 计算过程的向量化。通过运用线性代数知识详细的分析了网络的计算过程,并知道如何将计算向量化,并在代码中用向量化的方式来实现。这大大提高了网络的计算速度(因为numpy中的ndarray能够并行运算),同时也使得公式和程序看起来更简洁。
5. 对激活函数有了较深的理解。主要有为什么引入激活函数,激活函数必须的性质(非线性,单调,可导等),激活函数的饱和区间对网络训练的影响,几种激活函数(sigmoid,tanh,ReLU)的对比。
6. 提高了动手编程能力。只看书和看文章绝对没有这样深刻的印象,在动手的过程中才能真正的理解和掌握。
7. 体会到了神经网络的诸多影响因素对神经网络的意义。主要有:归一化,网络参数(W,b)初始化,超参数(学习速率,隐层数目,迭代次数,批次大小),激活函数等。





















 1593
1593

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








