数据结构、算法刷题笔记（2）（小白零基础、自用学习笔记）数组前缀篇python实现

题目一：

解题思路：

（1）用暴力穷举，用两个指针，将全部子数组的和求出，并且和K比较，相同则给计数器counter加1

（2）如何快速得到某个子数组的和呢？

这里就用到了数组前缀和的概念，对于一个给定的数组nums，我们将设置一个接口计算该数组的前缀和preSum，preSum[i]就是nums[0..i-1]的和。那么如果我们想求nums[i..j]的和，只需要一步操作preSum[j+1]-preSum[i]即可，而不需要重新去遍历数组了。

例如：nums=[1,0,-1]或[1,-1,0]

则前缀和preSum=[0, 1,1,0]或[0,1,0,0]

k = 0

我们先完成presum的接口（python代码）：

def presum(num):

preSum = []

preSum.append(0)

for i in range(len(num)):

preSum.append(preSum[i] + num[i])

return preSum

然后使用暴力穷举，计算所有子数组的和，并与K比较

def addnum(num,k):

sum = presum(num)#获得前缀和数组

counter = 0 #计数器初始值为0

i = 1 #while循环中的i

while i <= len(num): #一个指针在num数组中顺移

for j in range(i): #另一个指针在i之前顺移，可以穷举i之前的全部子数组

if sum[i] - sum[j] == k: # 当两个前缀和相减的值为K，则给计数器加1

counter = counter + 1

i = i + 1

return counter

（3）通过以上的代码，我们得到一个时间复杂度是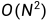的答案，接下来，我们开始优化代码。

我们主要优化方向就是，把循环改成一个，即将内循环中的j删掉：

j在循环中的作用是和i组成“边界”，我们可以计算“边界”内的和，j的使用条件是：

sum[i] - sum[j] == k

移项：sum[i] - k == sum[j]

也就是现在我们要用已经有的表示方法来代替sum[j]，j满足以下条件：①在i之前；②从0下标开始；③到sum[-2]截止，是前缀和。

解题思路如下：

这样我们编写优化后的代码：

def addnum_better(num,k):

sum = presum(num)

counter = 0

haxi = {0:1}#用字典存下每个前缀和出现的次数，初始值为{0:1}

i = 1

while i <= len(num):

if (sum[i] - k) in haxi.keys(): #范围内是否出现该前缀和

counter = haxi[sum[i]-k] + counter #记下前缀和出现的次数

haxi[sum[i]] = haxi.get(sum[i], 0) + 1#更新前缀和出现的次数

i = i + 1

return counter

这样，我们就得到了一个时间复杂度仅为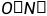的代码。

前缀和主要用于处理数组区间问题

题目二：

统计班上同学考试成绩在不同分数段的百分比，班上一共60个同学，满分是150分，给定数组score表示每个同学的分数，统计班上同学在给定分数段上的百分比。

score = [64, 103, 64, 58, 69, 40, 8, 117, 22, 6, 129, 50, 58, 135, 106, 113, 1, 82, 75, 75, 78, 89, 118, 113, 24, 98, 29, 103, 80, 133, 48, 134, 141, 123, 61, 82, 23, 15, 35, 23, 139, 102, 121, 10, 149, 15, 83, 62, 129, 7, 14, 144, 13, 146, 64, 70, 68, 137, 40, 52] #随机生成的

给定分数段 section = [40,80]

解题思路：

（1）求同学的百分比，也就是最后是统计人数。首先统计每个分数有多少人，分数的范围是[0,150]，即要明白构造谁的前缀和，构造每个分数上人数的数组：

count = [0 for i in range(151)] #得到一个长为151，全部都是0的数组

for i in score:

count[i] = count[i] + 1

（2）利用前缀和思想，构造前缀和precount:

precount = []

precount.append(0)

for i in range(len(count)):

precount.append(count[i]+precount[i])

（3）根据前缀和计算在某个分数段的人有多少：

section_counter = precount[k[1]+1] - precount[k[0]]