满二叉树 Vs 完全二叉树

满二叉树

如果二叉树中除了叶子结点，每个结点的度都为 2，则此二叉树称为满二叉树。

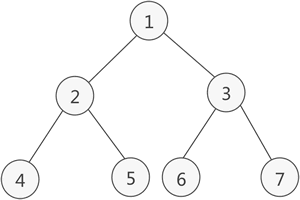
图 2 满二叉树示意图

如图 2 所示就是一棵满二叉树。

满二叉树除了满足普通二叉树的性质，还具有以下性质：

1. 满二叉树中第 i 层的节点数为 2n-1 个。
2. 深度为 k 的满二叉树必有 2k-1 个节点 ，叶子数为 2k-1。
3. 满二叉树中不存在度为 1 的节点，每一个分支点中都两棵深度相同的子树，且叶子节点都在最底层。
4. 具有 n 个节点的满二叉树的深度为 log2(n+1)。

完全二叉树

如果二叉树中除去最后一层节点为满二叉树，且最后一层的结点依次从左到右分布，则此二叉树被称为完全二叉树。

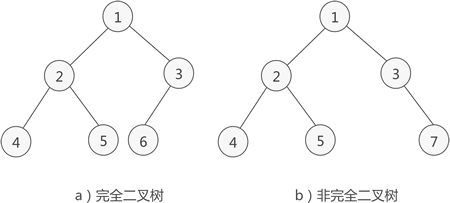
图 3 完全二叉树示意图

如图 3a) 所示是一棵完全二叉树，图 3b) 由于最后一层的节点没有按照从左向右分布，因此只能算作是普通的二叉树。

完全二叉树除了具有普通二叉树的性质，它自身也具有一些独特的性质，比如说，n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。

⌊log2n⌋ 表示取小于 log2n 的最大整数。例如，⌊log24⌋ = 2，而 ⌊log25⌋ 结果也是 2。