LCC: Learning to Customize and Combine Neural Networks for Few-Shot Learning 论文地址
写在前面
这篇论文是天津大学和新加坡国立合作的一篇 用meta-learning 做 few-shot learning 的文章, 算是我看的meta-learning的文章中写的比较接地气的,比较好看懂的文章, 看了这篇文章基本就可以知道 few-shot learning 以及meta-learning 是做什么的. 主要还是学习一种更好更快的adaption, transfer的算法.
Motivation
- 由于现实应用中数据太少, 所以需要寻求好的few-shot learning的方法, 但是也是由于数据太少的关系, few-shot learning很难达到高的精度;
- meta-learning是一种可以利用已有经验的方式, 可以将知识从相似的few-shot learning的任务中迁移过来;
- 传统的few-shot learning任务中的base-learner 是很不稳定的, 所以这篇文章使用集成学习的方式,利用meta-learning来选择base-learner.
Contribution
- 提出了一个novel的meta-learning方式去学习如何集成多个base-learner来处理few-shot learning task;
- 他们做了很多实验, 证明了很多 automatic adaption 的技巧, 比如后期的学习率应该比前期的大等.
Preliminary
这一节先简单介绍了few-shot learning的总体的公式和流程, 然后介绍了meta-learning中的一些概念.
1. episodic formulation
其实这个episode不用太纠结是什么, 把一个task当成是一个episode就行了. few-shot learning和传统的分类问题主要有以下三点区别:
- 训练集不同, 在few-shot learning中, 数据被分成 meta-train 和 meta-test 两个部分, 每个部分都有train 和test 数据;
- meta-train 和 meta-test 中的sample不是简单的数据点, 而是每个episode (也就是task);
- few-shot learning 的目标不是为了分类没见过的数据, 而是为了快速将学到的经验adapt到新的任务上.
meta-train的过程:
对于一个数据集, 我们先采样few-shot tasks
{
T
}
\{T\}
{T}, 对于每个task, 将其分成
T
(
t
r
)
T^{(tr)}
T(tr) :用来优化一个base-learner, 和
T
(
t
e
)
T^{(te)}
T(te) : 来计算一个generalization 的loss来优化meta-learner.
meta-testing 过程:
meta-test数据集 (
T
u
n
T_{un}
Tun) 中的类别和meta-learn数据集中的类别没有重叠. 然后用 meta-test中train数据 (
T
u
n
(
t
r
)
T_{un}^{(tr)}
Tun(tr)) 来训练之前预训练的模型, 最后用meta-test中的test数据 (
T
u
n
(
t
e
)
T_{un}^{(te)}
Tun(te)) 来评估这个few-shot learning的性能.
2. Meta gradient decent
说是meta 梯度下降, 其实就是用的二阶梯度来实现的, 对于一个episode
T
=
{
T
(
t
r
)
,
T
(
t
e
)
}
T = \{T^{(tr)}, T^{(te)}\}
T={T(tr),T(te)} , 先将base-learner的参数
Θ
\Theta
Θ 初始化为
θ
\theta
θ , 即
Θ
0
=
θ
\Theta_0 = \theta
Θ0=θ, 然后用训练数据集
T
(
t
r
)
T^{(tr)}
T(tr) 中的loss来更新这些参数:
Θ
m
+
1
←
Θ
m
−
α
∇
Θ
m
L
λ
(
T
(
t
r
)
,
Θ
m
)
\Theta_{m+1} \leftarrow \Theta_m - \alpha \nabla_{\Theta_m} L_{\lambda}(T^{(tr)}, \Theta_m)
Θm+1←Θm−α∇ΘmLλ(T(tr),Θm)
其中
L
λ
L_\lambda
Lλ 是对固定超参
λ
\lambda
λ 的惩罚,
α
\alpha
α 是固定的学习率,
m
m
m 值得第
m
m
m 个epoch. 在训练
M
M
M 个epoch后, 用
T
(
t
e
)
T^{(te)}
T(te) 去算一个验证集的loss来更新
θ
\theta
θ :
θ
=
:
θ
−
β
∇
θ
L
λ
(
T
(
t
e
)
,
Θ
m
)
\theta=:\theta - \beta \nabla_{\theta}L_{\lambda} (T^{(te)}, \Theta_m)
θ=:θ−β∇θLλ(T(te),Θm)
这里对 θ \theta θ的梯度计算是从 Θ m \Theta_m Θm到 Θ 0 \Theta_0 Θ0的, 这里用到了Hessian矩阵来算二阶梯度, 不过文章中没有细讲这个, 就说他们用了tensorflow中的库实现的, 具体可能需要等开源了才知道了.
Algorithm
下图是这篇文章的主要流程, 可以看到这篇文章不仅学了一系列的base-learner, 也学了如何将这些base-learner结合起来, 去达到最好的performance.
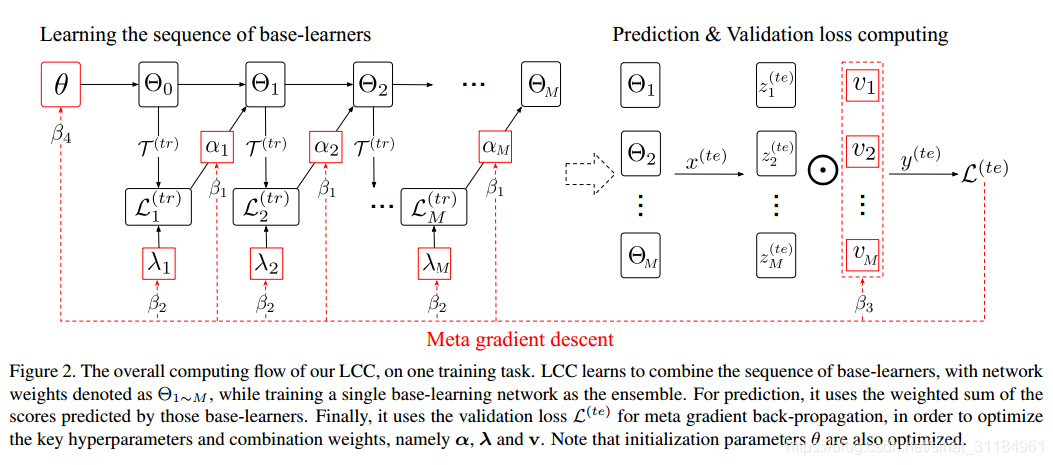
其实这篇文章说的多个base-learner就是一个网络的不同epoch, 一共训练
M
M
M个epoch, 就有
M
M
M 个base-learner, 每个base-learner拥有自己的学习率
α
m
\alpha_m
αm 和超参
λ
m
\lambda_m
λm(这两个参数是通过meta-learning学出来的) , 总的网络更新的流程如下:
Θ
0
←
θ
,
\Theta_0 \leftarrow \theta,
Θ0←θ,
Θ
m
←
Θ
m
−
1
−
α
m
∇
Θ
L
m
(
t
r
)
.
\Theta_m \leftarrow \Theta_{m-1}-\alpha_m \nabla_{\Theta} L_m^{(tr)}.
Θm←Θm−1−αm∇ΘLm(tr).
如果用
F
(
x
;
Θ
m
)
F(x;\Theta_m)
F(x;Θm)来表示第m个Base-learner预测出来的结果, 那这个base-learner对应的损失为:
L
m
(
t
r
)
=
1
N
1
∑
j
=
1
N
1
L
c
e
(
F
(
x
;
Θ
m
−
1
,
y
i
(
t
r
)
)
+
λ
m
∣
∣
Θ
m
−
1
∣
∣
2
2
.
L_m^{(tr)} = \frac{1}{N_1}\sum_{j=1}^{N_1}L_{ce} (F(x;\Theta_{m-1}, y_i^{(tr)})+\lambda_m ||\Theta_{m-1}||_2^2.
Lm(tr)=N11j=1∑N1Lce(F(x;Θm−1,yi(tr))+λm∣∣Θm−1∣∣22.
其中
N
1
N_1
N1表示
T
(
t
r
)
T^{(tr)}
T(tr)中的样本个数.
1. Learn to customize base-learners
这边文中提到了, 使用layer-wise的学习率和正则化参数
λ
\lambda
λ 会使得网络精度更高, 这里使用
T
(
t
e
)
T^{(te)}
T(te)来更新
α
\alpha
α 和
λ
\lambda
λ, 其中loss的计算方式如下:
L
(
t
e
)
=
1
N
2
∑
j
=
1
N
2
L
c
e
(
y
^
j
(
t
e
)
,
y
j
(
t
e
)
)
L^{(te)} = \frac{1}{N_2}\sum_{j=1}^{N_2}L_{ce}(\hat{y}_j^{(te)}, y_j^{(te)})
L(te)=N21j=1∑N2Lce(y^j(te),yj(te))
其中
N
2
N_2
N2表示当前的
T
(
t
e
)
T^{(te)}
T(te) 中的样本个数.
y
^
j
(
t
e
)
\hat{y}_j^{(te)}
y^j(te)是集成了
M
M
M个base-learner的总的预测结果, 参数更新过程如下:
α
=
:
α
−
β
1
∇
α
L
(
t
e
)
,
λ
=
:
λ
−
β
2
∇
λ
L
(
t
e
)
\alpha = :\alpha - \beta_1 \nabla_{\alpha} L^{(te)}, \lambda = :\lambda - \beta_2 \nabla_{\lambda}L^{(te)}
α=:α−β1∇αL(te),λ=:λ−β2∇λL(te)
2. Learn to combine base-learners
这节介绍了如何将这些base-learner集成起来, 这里定义了一个权重参数
v
=
{
v
m
}
m
=
1
M
v = \{v_m\}_{m=1}^M
v={vm}m=1M, 也就是每个base-learner都有一个权重, 假设
z
z
z是由这些base-learner共同预测出来的结果, 那么
z
z
z的计算如下:
z
=
∑
m
=
1
M
v
m
F
(
x
;
Θ
m
)
,
z = \sum_{m=1}^M v_m F(x; \Theta_m),
z=m=1∑MvmF(x;Θm),
v的更新过程:
v
=
:
v
−
β
3
∇
v
L
(
t
e
)
v = :v-\beta_3 \nabla_v L^{(te)}
v=:v−β3∇vL(te)
根据以上的式子,
L
(
t
e
)
L^{(te)}
L(te)的计算可以写成:
L
(
t
e
)
=
1
N
2
∑
j
=
1
N
2
L
c
e
(
∑
m
=
1
M
v
m
F
(
x
;
Θ
m
)
,
y
j
(
t
e
)
)
L^{(te)} = \frac{1}{N_2}\sum_{j=1}^{N_2}L_{ce}( \sum_{m=1}^M v_m F(x; \Theta_m), y_j^{(te)})
L(te)=N21j=1∑N2Lce(m=1∑MvmF(x;Θm),yj(te))
3. 总的更新步骤
总的参数更新流程可以抽象总结为:
[
θ
;
α
;
λ
;
v
]
=
:
[
θ
;
α
;
λ
;
v
]
−
β
⊙
∇
L
m
e
t
a
[\theta;\alpha;\lambda;v] = :[\theta;\alpha;\lambda;v] - \beta \odot \nabla L_{meta}
[θ;α;λ;v]=:[θ;α;λ;v]−β⊙∇Lmeta
L
m
e
t
a
=
1
P
∑
i
=
1
P
L
(
T
i
(
t
e
)
;
α
,
λ
,
v
)
L_{meta} = \frac{1}{P}\sum_{i=1}^P L(T_i^{(te)};\alpha, \lambda, v)
Lmeta=P1i=1∑PL(Ti(te);α,λ,v)
其中P代表episode的个数, 也就是这个
L
m
e
t
a
L_{meta}
Lmeta是根据多个episode计算出来的.
文章总的算法流程如下:


这两个流程写的比较仔细也很容易可以看懂
Experiment
这里我简单放两张图, 具体看原文, 文章后面做了很多实验去分析了超参的一些规律, 对很多网络学习任务可能都有一定的帮助.
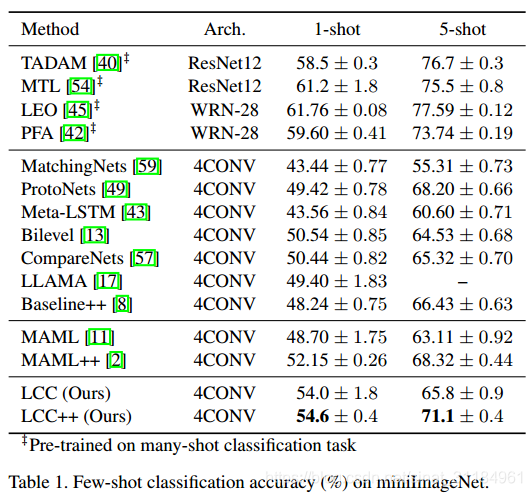
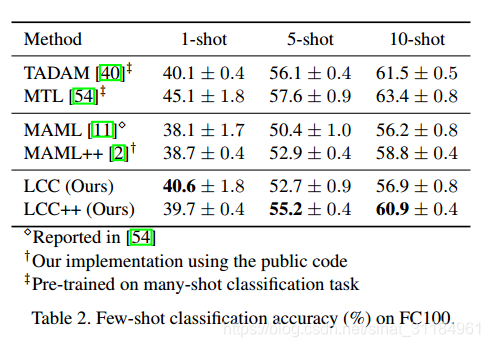




 本文介绍了一种名为LCC的新型元学习方法,旨在解决小样本学习问题。通过集成多个基学习器并定制其参数,LCC能够更有效地适应新任务,实现在少量数据上的高效学习。
本文介绍了一种名为LCC的新型元学习方法,旨在解决小样本学习问题。通过集成多个基学习器并定制其参数,LCC能够更有效地适应新任务,实现在少量数据上的高效学习。
















 1140
1140

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








