「POJ3067」 Japan - 树状数组

原创于 2018-09-14 22:01:24 发布 · 258 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#树状数组 #逆序对 #排序

数据结构---树状数组专栏收录该内容

5 篇文章

订阅专栏

探讨了日本为ACMICPC世界总决赛规划道路的问题，通过计算高速公路交叉口数量来优化建设成本。使用树状数组求解逆序对，实现高效的算法设计。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目大意

日本计划欢迎ACM ICPC世界总决赛，并且必须为场地建造很多道路。日本是一个高岛，东海岸有N个城市，西海岸有M市（M<＝1000，N<＝1000）。将修建K级高速公路。每个海岸的城市编号为1, 2，…从北方到南方。每一条高速公路都是直线，连接东海岸的城市和西海岸的城市。建设资金由ACM保证。总和的主要部分由高速公路之间的交叉数决定。最多两条高速公路在一处交叉。编写一个计算高速公路交叉口数量的程序。（原文为英文，本文为机翻）。

分析

我们把每一条边按照左端点从小到大排序，相同则按照右端点从小到大排序，然后可以发现，若两条边相交，则在排序后的右端点为一组逆序对。为什么？可以想想，对于两条边（a1,b1）,（a2,b2）,现在已经保证了a1<a2，若b1>b2，这两条边就能相交。如下图。

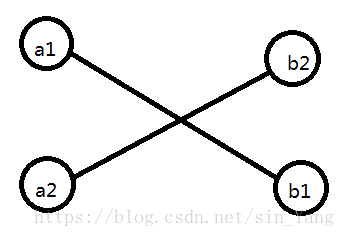
Japan

然后就可以用树状数组求逆序对了。

分析

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;
struct Node {
	int x,y;
}e[1000*1000+5];
int n,m,k,t;
long long ans;
int c[100005];
int lowbit(int x) {
	return x&-x;
}
void update(int x,int y) {
	while (x<=m) {
		c[x]+=y;
		x+=lowbit(x);
	}
}
int sum(int x) {
	int ret=0;
	while (x) {
		ret+=c[x];
		x-=lowbit(x);
	}
	return ret;
}
bool cmp(Node a,Node b) {
	return a.x!=b.x?a.x<b.x:a.y<b.y;
}
int main() {
	scanf("%d",&t);
	for (int j=1;j<=t;j++) {
		memset(c,0,sizeof c);
		ans=0;
		scanf("%d%d%d",&n,&m,&k);
		for (int i=1;i<=k;i++)
			scanf("%d%d",&e[i].x,&e[i].y);
		sort(e+1,e+k+1,cmp);
		for (int i=k;i>=1;i--) {
			ans+=sum(e[i].y-1);
			update(e[i].y,1);
		}
		printf("Test case %d: %lld",j,ans);
		if (j<t) puts("");
	}
	return 0;
}