16.
确定方程组是否相容:
{x1−2x4=−32x2+2x3=0x3+3x4=1−2x1+3x2+2x3+x4=5 \begin{cases} x_1 - 2x_4 = -3 \\ 2x_2 + 2x_3 = 0 \\ x_3 + 3x_4 = 1 \\ -2x_1 + 3x_2 + 2x_3 + x_4 = 5 \end{cases} ⎩⎨⎧x1−2x4=−32x2+2x3=0x3+3x4=1−2x1+3x2+2x3+x4=5
增广矩阵:
[100−2−30220000131−23215]
\begin{bmatrix}
1 & 0 & 0 & -2 & -3 \\
0 & 2 & 2 & 0 & 0 \\
0 & 0 & 1 & 3 & 1 \\
-2 & 3 & 2 & 1 & 5
\end{bmatrix}
100−202030212−2031−3015
行变换过程:
-
将第四行替换为 R4+2R1R_4 + 2R_1R4+2R1:
[100−2−30220000131032−3−1] \begin{bmatrix} 1 & 0 & 0 & -2 & -3 \\ 0 & 2 & 2 & 0 & 0 \\ 0 & 0 & 1 & 3 & 1 \\ 0 & 3 & 2 & -3 & -1 \end{bmatrix} 100002030212−203−3−301−1 -
将第四行替换为 R4+(−32)R2R_4 + \left(-\frac{3}{2}\right)R_2R4+(−23)R2:
[100−2−3022000013100−1−3−1] \begin{bmatrix} 1 & 0 & 0 & -2 & -3 \\ 0 & 2 & 2 & 0 & 0 \\ 0 & 0 & 1 & 3 & 1 \\ 0 & 0 & -1 & -3 & -1 \end{bmatrix} 10000200021−1−203−3−301−1 -
将第四行替换为 R4+R3R_4 + R_3R4+R3:
[100−2−3022000013100000] \begin{bmatrix} 1 & 0 & 0 & -2 & -3 \\ 0 & 2 & 2 & 0 & 0 \\ 0 & 0 & 1 & 3 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{bmatrix} 100002000210−2030−3010
结论:
行阶梯形中无矛盾方程(即无 0=k0 = k0=k 形式的行),且前三行均有主元。
方程组相容,有无穷多解。
17.
三条直线 x1−4x2=1x_1 - 4x_2 = 1x1−4x2=1,2x1−x2=−32x_1 - x_2 = -32x1−x2=−3 和 −x1−3x2=4-x_1 - 3x_2 = 4−x1−3x2=4 是否有交点?
增广矩阵:
[1−412−1−3−1−34]
\begin{bmatrix}
1 & -4 & 1 \\
2 & -1 & -3 \\
-1 & -3 & 4
\end{bmatrix}
12−1−4−1−31−34
行变换过程:
-
将第二行替换为 R2−2R1R_2 - 2R_1R2−2R1:
[1−4107−5−1−34] \begin{bmatrix} 1 & -4 & 1 \\ 0 & 7 & -5 \\ -1 & -3 & 4 \end{bmatrix} 10−1−47−31−54 -
将第三行替换为 R3+R1R_3 + R_1R3+R1:
[1−4107−50−75] \begin{bmatrix} 1 & -4 & 1 \\ 0 & 7 & -5 \\ 0 & -7 & 5 \end{bmatrix} 100−47−71−55 -
将第三行替换为 R3+R2R_3 + R_2R3+R2:
[1−4107−5000] \begin{bmatrix} 1 & -4 & 1 \\ 0 & 7 & -5 \\ 0 & 0 & 0 \end{bmatrix} 100−4701−50
结论:
行阶梯形中无矛盾方程,且主元数量等于变量数。
系统相容且有唯一解,三条直线交于一点。
18.
三条直线 x1+2x2+x3=4x_1 + 2x_2 + x_3 = 4x1+2x2+x3=4,x2−x3=1x_2 - x_3 = 1x2−x3=1 和 x1+3x2=0x_1 + 3x_2 = 0x1+3x2=0 是否有交点?
增广矩阵:
[121401−111300]
\begin{bmatrix}
1 & 2 & 1 & 4 \\
0 & 1 & -1 & 1 \\
1 & 3 & 0 & 0
\end{bmatrix}
1012131−10410
行变换过程:
-
将第三行替换为 R3−R1R_3 - R_1R3−R1:
[121401−1101−1−4] \begin{bmatrix} 1 & 2 & 1 & 4 \\ 0 & 1 & -1 & 1 \\ 0 & 1 & -1 & -4 \end{bmatrix} 1002111−1−141−4 -
将第三行替换为 R3−R2R_3 - R_2R3−R2:
[121401−11000−5] \begin{bmatrix} 1 & 2 & 1 & 4 \\ 0 & 1 & -1 & 1 \\ 0 & 0 & 0 & -5 \end{bmatrix} 1002101−1041−5
矛盾分析:
第三行对应方程 0x1+0x2+0x3=−50x_1 + 0x_2 + 0x_3 = -50x1+0x2+0x3=−5,即 0=−50 = -50=−5,为矛盾方程。
结论:
系统包含矛盾方程。
三条直线无共同交点。
19.
确定 hhh 的值,使得矩阵是某个相容线性方程组的增广矩阵:
[1h4368] \begin{bmatrix} 1 & h & 4 \\ 3 & 6 & 8 \end{bmatrix} [13h648]
行变换过程:
- 将第二行替换为 R2−3R1R_2 - 3R_1R2−3R1:
[1h406−3h−4] \begin{bmatrix} 1 & h & 4 \\ 0 & 6-3h & -4 \end{bmatrix} [10h6−3h4−4]
相容性分析:
- 当 6−3h≠06-3h \neq 06−3h=0(即 h≠2h \neq 2h=2)时,系统相容,有唯一解。
- 当 h=2h = 2h=2 时,第二行变为 [0 0 −4][0\ 0\ -4][0 0 −4],对应方程 0=−40 = -40=−4,矛盾。
结论:
当且仅当 h≠2h \neq 2h=2 时,方程组相容。
20.
确定 hhh 的值,使得矩阵是某个相容线性方程组的增广矩阵:
[1h−3−246] \begin{bmatrix} 1 & h & -3 \\ -2 & 4 & 6 \end{bmatrix} [1−2h4−36]
行变换过程:
- 将第二行替换为 R2+2R1R_2 + 2R_1R2+2R1:
[1h−304+2h0] \begin{bmatrix} 1 & h & -3 \\ 0 & 4+2h & 0 \end{bmatrix} [10h4+2h−30]
相容性分析:
- 第二行对应方程 (4+2h)x2=0(4+2h)x_2 = 0(4+2h)x2=0。
- 若 4+2h≠04+2h \neq 04+2h=0,则 x2=0x_2 = 0x2=0,系统相容。
- 若 4+2h=04+2h = 04+2h=0(即 h=−2h = -2h=−2),则方程为 0=00 = 00=0,x2x_2x2 可取任意值,系统仍相容。
结论:
对任意 hhh,方程组均相容。
21.
确定 hhh 的值,使得矩阵是某个相容线性方程组的增广矩阵:
[13−2−4h8] \begin{bmatrix} 1 & 3 & -2 \\ -4 & h & 8 \end{bmatrix} [1−43h−28]
行变换过程:
- 将第二行替换为 R2+4R1R_2 + 4R_1R2+4R1:
[13−20h+120] \begin{bmatrix} 1 & 3 & -2 \\ 0 & h+12 & 0 \end{bmatrix} [103h+12−20]
相容性分析:
- 第二行对应方程 (h+12)x2=0(h+12)x_2 = 0(h+12)x2=0。
- 若 h+12≠0h+12 \neq 0h+12=0,则 x2=0x_2 = 0x2=0,系统相容。
- 若 h+12=0h+12 = 0h+12=0(即 h=−12h = -12h=−12),则方程为 0=00 = 00=0,x2x_2x2 可取任意值,系统仍相容。
结论:
对任意 hhh,方程组均相容。
22.
确定 hhh 的值,使得矩阵是某个相容线性方程组的增广矩阵:
[2−3h−695] \begin{bmatrix} 2 & -3 & h \\ -6 & 9 & 5 \end{bmatrix} [2−6−39h5]
行变换过程:
- 将第二行替换为 R2+3R1R_2 + 3R_1R2+3R1:
[2−3h005+3h] \begin{bmatrix} 2 & -3 & h \\ 0 & 0 & 5+3h \end{bmatrix} [20−30h5+3h]
相容性分析:
- 当 5+3h=05+3h = 05+3h=0(即 h=−53h = -\frac{5}{3}h=−35)时,第二行变为 [0 0 0][0\ 0\ 0][0 0 0],系统相容(有无穷多解)。
- 当 5+3h≠05+3h \neq 05+3h=0 时,第二行对应方程 0=5+3h0 = 5+3h0=5+3h,矛盾,系统不相容。
结论:
当且仅当 h=−53h = -\frac{5}{3}h=−35 时,方程组相容。
23.
判断下列命题的真假,并说明理由:
a. 每个矩阵行变换都是可逆的。
b. 5×65 \times 65×6 矩阵有 6 行。
c. 包含 nnn 个变量 x1,x2,…,xnx_1, x_2, \dots, x_nx1,x2,…,xn 的线性方程组的解集是一组数 (s1,s2,…,sn)(s_1, s_2, \dots, s_n)(s1,s2,…,sn),当用这组数代替 x1,x2,…,xnx_1, x_2, \dots, x_nx1,x2,…,xn 时,方程组中每个方程成为恒等式。
d. 线性方程组的两个基本问题涉及存在性和唯一性。
解答:
-
a. True
教材中“Elementary Row Operations”框后的说明指出:每个初等行变换都是可逆的。例如,交换两行的逆变换是再次交换这两行;某行乘以非零常数 kkk 的逆变换是乘以 1/k1/k1/k;某行加上另一行的 kkk 倍的逆变换是减去该行的 kkk 倍。 -
b. False
5×65 \times 65×6 矩阵表示有 5 行、6 列,而非 6 行。矩阵维度的定义是“行数 × 列数”,因此该命题错误。 -
c. False
该描述仅适用于单个解,但解集是所有可能解的集合。例如,相容且有无穷多解的方程组,其解集包含无限多个解;只有当解集恰好只含一个解时,该描述才成立。因此该命题不完全正确。 -
d. True
教材中 Example 2 前的框中明确指出:线性方程组的两个基本问题为存在性(是否有解)和唯一性(解是否唯一)。
24.
判断下列命题的真假,并说明理由:
a. 对增广矩阵的初等行变换不会改变相关的线性方程组的解集。
b. 两个矩阵是行等价的,若它们有相同的行数。
c. 不相容线性方程组有一个或更多解。
d. 两个线性方程组是等价的,若它们有相同的解集。
解答:
-
a. True
教材中“Existence and Uniqueness Questions”小节前的框中明确说明:初等行变换不会改变线性方程组的解集。这是因为每个初等行变换对应方程组的等价变形(如交换方程、方程两边同乘非零常数、方程相加),不改变方程的解。 -
b. False
行等价的定义要求:存在一系列初等行变换将一个矩阵转换为另一个矩阵,而不仅仅是行数相同。例如,两个行数相同的矩阵若无法通过行变换相互转换,则不是行等价的。因此该命题错误。 -
c. False
根据定义,不相容系统没有解。若方程组存在矛盾方程(如 0=10 = 10=1),则无解,因此“有一个或更多解”的说法与定义矛盾。 -
d. True
教材中方程 (2) 后第二段明确给出等价系统的定义:两个线性方程组是等价的,当且仅当它们有相同的解集。这是等价系统的核心定义。
25.
求出包含 ggg、hhh 和 kkk 的方程,使以下矩阵是相容方程组的增广矩阵:
[1−47g03−5h−25−9k] \begin{bmatrix} 1 & -4 & 7 & g \\ 0 & 3 & -5 & h \\ -2 & 5 & -9 & k \end{bmatrix} 10−2−4357−5−9ghk
行变换过程:
-
将第三行替换为 R3+2R1R_3 + 2R_1R3+2R1:
[1−47g03−5h0−35k+2g] \begin{bmatrix} 1 & -4 & 7 & g \\ 0 & 3 & -5 & h \\ 0 & -3 & 5 & k+2g \end{bmatrix} 100−43−37−55ghk+2g -
将第三行替换为 R3+R2R_3 + R_2R3+R2:
[1−47g03−5h000k+2g+h] \begin{bmatrix} 1 & -4 & 7 & g \\ 0 & 3 & -5 & h \\ 0 & 0 & 0 & k+2g+h \end{bmatrix} 100−4307−50ghk+2g+h
相容性分析:
- 第三行对应方程 0=k+2g+h0 = k + 2g + h0=k+2g+h。
- 为使方程组相容,必须满足 k+2g+h=0k + 2g + h = 0k+2g+h=0。
结论:
当且仅当 k+2g+h=0k + 2g + h = 0k+2g+h=0 时,方程组相容。
26.
给解集为 x1=−2x_1 = -2x1=−2、x2=1x_2 = 1x2=1、x3=0x_3 = 0x3=0 的线性方程组构造三个不同的增广矩阵。
构造方法:
利用初等行变换不改变解集的性质,从最简形式出发,通过不同行变换生成新矩阵。
三个增广矩阵:
-
最简形式:
[100−201010010] \begin{bmatrix} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} 100010001−210 -
对第一行进行变换:
[100−2210−30010](第二行替换为 R2+2R1) \begin{bmatrix} 1 & 0 & 0 & -2 \\ 2 & 1 & 0 & -3 \\ 0 & 0 & 1 & 0 \end{bmatrix} \quad \text{(第二行替换为 $R_2 + 2R_1$)} 120010001−2−30(第二行替换为 R2+2R1) -
对第二行进行变换:
[100−20101201−4](第三行替换为 R3+2R1) \begin{bmatrix} 1 & 0 & 0 & -2 \\ 0 & 1 & 0 & 1 \\ 2 & 0 & 1 & -4 \end{bmatrix} \quad \text{(第三行替换为 $R_3 + 2R_1$)} 102010001−21−4(第三行替换为 R3+2R1)
结论:
以上三个矩阵均与最简形式行等价,因此解集均为 (−2,1,0)(-2, 1, 0)(−2,1,0)。
27.
设方程组对所有 fff 和 ggg 的可能取值都相容,求系数 ccc 和 ddd 的特性:
{x1+3x2=fcx1+dx2=g \begin{cases} x_1 + 3x_2 = f \\ cx_1 + dx_2 = g \end{cases} {x1+3x2=fcx1+dx2=g
增广矩阵:
[13fcdg]
\begin{bmatrix}
1 & 3 & f \\
c & d & g
\end{bmatrix}
[1c3dfg]
行变换过程:
- 将第二行替换为 R2−cR1R_2 - cR_1R2−cR1:
[13f0d−3cg−cf] \begin{bmatrix} 1 & 3 & f \\ 0 & d-3c & g-cf \end{bmatrix} [103d−3cfg−cf]
相容性分析:
- 为使方程组对任意 fff 和 ggg 相容,第二行不能出现矛盾方程 0=b0 = b0=b(其中 b≠0b \neq 0b=0)。
- 因此需保证 d−3c≠0d - 3c \neq 0d−3c=0,否则当 g−cf≠0g - cf \neq 0g−cf=0 时,方程组无解。
结论:
系数必须满足 d≠3cd \neq 3cd=3c。
28.
设 a≠0a \neq 0a=0,方程组对所有 fff 和 ggg 的可能取值都相容,求系数 a,b,c,da, b, c, da,b,c,d 的特性:
{ax1+bx2=fcx1+dx2=g \begin{cases} ax_1 + bx_2 = f \\ cx_1 + dx_2 = g \end{cases} {ax1+bx2=fcx1+dx2=g
增广矩阵:
[abfcdg]
\begin{bmatrix}
a & b & f \\
c & d & g
\end{bmatrix}
[acbdfg]
行变换过程:
-
将第一行缩放为 1aR1\frac{1}{a}R_1a1R1(因 a≠0a \neq 0a=0):
[1b/af/acdg] \begin{bmatrix} 1 & b/a & f/a \\ c & d & g \end{bmatrix} [1cb/adf/ag] -
将第二行替换为 R2−cR1R_2 - cR_1R2−cR1:
[1b/af/a0d−c(b/a)g−c(f/a)] \begin{bmatrix} 1 & b/a & f/a \\ 0 & d - c(b/a) & g - c(f/a) \end{bmatrix} [10b/ad−c(b/a)f/ag−c(f/a)]
相容性分析:
-
为使方程组对任意 fff 和 ggg 相容,需保证 d−c(b/a)≠0d - c(b/a) \neq 0d−c(b/a)=0。
-
化简条件:
d−bca≠0⇒ad−bc≠0 d - \frac{bc}{a} \neq 0 \quad \Rightarrow \quad ad - bc \neq 0 d−abc=0⇒ad−bc=0
结论:
系数必须满足 ad≠bcad \neq bcad=bc(即系数矩阵行列式非零)。
29.
第一个矩阵变为第二个矩阵:
[0−2514−73−16]→[14−70−253−16] \begin{bmatrix} 0 & -2 & 5 \\ 1 & 4 & -7 \\ 3 & -1 & 6 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 4 & -7 \\ 0 & -2 & 5 \\ 3 & -1 & 6 \end{bmatrix} 013−24−15−76→1034−2−1−756
初等行变换:
交换第一行与第二行(R1↔R2R_1 \leftrightarrow R_2R1↔R2)。
第二个矩阵变回第一个矩阵:
逆变换:
交换第一行与第二行(R1↔R2R_1 \leftrightarrow R_2R1↔R2)(交换操作自逆)。
30.
第一个矩阵变为第二个矩阵:
[13−40−260−59]→[13−401−30−59] \begin{bmatrix} 1 & 3 & -4 \\ 0 & -2 & 6 \\ 0 & -5 & 9 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 3 & -4 \\ 0 & 1 & -3 \\ 0 & -5 & 9 \end{bmatrix} 1003−2−5−469→10031−5−4−39
初等行变换:
将第二行缩放为 −12R2-\frac{1}{2}R_2−21R2(即 R2←−12R2R_2 \leftarrow -\frac{1}{2}R_2R2←−21R2)。
第二个矩阵变回第一个矩阵:
逆变换:
将第二行缩放为 −2R2-2R_2−2R2(即 R2←−2R2R_2 \leftarrow -2R_2R2←−2R2)。
31.
第一个矩阵变为第二个矩阵:
[1−21005−284−13−6]→[1−21005−2807−16] \begin{bmatrix} 1 & -2 & 1 & 0 \\ 0 & 5 & -2 & 8 \\ 4 & -1 & 3 & -6 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & -2 & 1 & 0 \\ 0 & 5 & -2 & 8 \\ 0 & 7 & -1 & 6 \end{bmatrix} 104−25−11−2308−6→100−2571−2−1086
初等行变换:
将第三行替换为 R3−4R1R_3 - 4R_1R3−4R1(即 R3←R3−4R1R_3 \leftarrow R_3 - 4R_1R3←R3−4R1)。
第二个矩阵变回第一个矩阵:
逆变换:
将第三行替换为 R3+4R1R_3 + 4R_1R3+4R1(即 R3←R3+4R1R_3 \leftarrow R_3 + 4R_1R3←R3+4R1)。
32.
第一个矩阵变为第二个矩阵:
[12−5001−3−20−395]→[12−5001−3−2000−1] \begin{bmatrix} 1 & 2 & -5 & 0 \\ 0 & 1 & -3 & -2 \\ 0 & -3 & 9 & 5 \end{bmatrix} \rightarrow \begin{bmatrix} 1 & 2 & -5 & 0 \\ 0 & 1 & -3 & -2 \\ 0 & 0 & 0 & -1 \end{bmatrix} 10021−3−5−390−25→100210−5−300−2−1
初等行变换:
将第三行替换为 R3+3R2R_3 + 3R_2R3+3R2(即 R3←R3+3R2R_3 \leftarrow R_3 + 3R_2R3←R3+3R2)。
第二个矩阵变回第一个矩阵:
逆变换:
将第三行替换为 R3−3R2R_3 - 3R_2R3−3R2(即 R3←R3−3R2R_3 \leftarrow R_3 - 3R_2R3←R3−3R2)。
33.
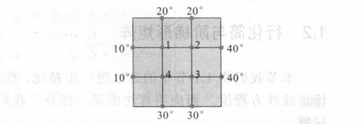
写出温度 T1,T2,T3,T4T_1, T_2, T_3, T_4T1,T2,T3,T4 所满足的方程组。
方程组推导:
每个内部结点的温度近似等于与其最接近的4个结点(上、下、左、右)的平均值。
-
T1T_1T1(左上结点):
上方 =20∘= 20^\circ=20∘,左方 =10∘= 10^\circ=10∘,下方 =T4= T_4=T4,右方 =T2= T_2=T2
T1=10+20+T2+T44⇒4T1−T2−T4=30 T_1 = \frac{10 + 20 + T_2 + T_4}{4} \quad \Rightarrow \quad 4T_1 - T_2 - T_4 = 30 T1=410+20+T2+T4⇒4T1−T2−T4=30 -
T2T_2T2(右上结点):
上方 =20∘= 20^\circ=20∘,左方 =T1= T_1=T1,下方 =T3= T_3=T3,右方 =40∘= 40^\circ=40∘
T2=20+T1+T3+404⇒4T2−T1−T3=60 T_2 = \frac{20 + T_1 + T_3 + 40}{4} \quad \Rightarrow \quad 4T_2 - T_1 - T_3 = 60 T2=420+T1+T3+40⇒4T2−T1−T3=60 -
T3T_3T3(右下结点):
上方 =T2= T_2=T2,左方 =T4= T_4=T4,下方 =30∘= 30^\circ=30∘,右方 =40∘= 40^\circ=40∘
T3=T2+T4+30+404⇒4T3−T2−T4=70 T_3 = \frac{T_2 + T_4 + 30 + 40}{4} \quad \Rightarrow \quad 4T_3 - T_2 - T_4 = 70 T3=4T2+T4+30+40⇒4T3−T2−T4=70 -
T4T_4T4(左下结点):
上方 =T1= T_1=T1,左方 =10∘= 10^\circ=10∘,下方 =30∘= 30^\circ=30∘,右方 =T3= T_3=T3
T4=T1+10+30+T34⇒4T4−T1−T3=40 T_4 = \frac{T_1 + 10 + 30 + T_3}{4} \quad \Rightarrow \quad 4T_4 - T_1 - T_3 = 40 T4=4T1+10+30+T3⇒4T4−T1−T3=40
完整方程组:
{4T1−T2−T4=30−T1+4T2−T3=60−T2+4T3−T4=70−T1−T3+4T4=40
\begin{cases}
4T_1 - T_2 - T_4 = 30 \\
-T_1 + 4T_2 - T_3 = 60 \\
-T_2 + 4T_3 - T_4 = 70 \\
-T_1 - T_3 + 4T_4 = 40
\end{cases}
⎩⎨⎧4T1−T2−T4=30−T1+4T2−T3=60−T2+4T3−T4=70−T1−T3+4T4=40
34.
解习题 33 中的方程组。
增广矩阵:
[4−10−130−14−10600−14−170−10−1440]
\begin{bmatrix}
4 & -1 & 0 & -1 & 30 \\
-1 & 4 & -1 & 0 & 60 \\
0 & -1 & 4 & -1 & 70 \\
-1 & 0 & -1 & 4 & 40
\end{bmatrix}
4−10−1−14−100−14−1−10−1430607040
行变换过程:
-
交换第一行与第四行(R1↔R4R_1 \leftrightarrow R_4R1↔R4):
[−10−1440−14−10600−14−1704−10−130] \begin{bmatrix} -1 & 0 & -1 & 4 & 40 \\ -1 & 4 & -1 & 0 & 60 \\ 0 & -1 & 4 & -1 & 70 \\ 4 & -1 & 0 & -1 & 30 \end{bmatrix} −1−10404−1−1−1−14040−1−140607030 -
缩放第一行 (−1)R1(-1)R_1(−1)R1,第二行 (−1)R2(-1)R_2(−1)R2,并将第四行替换为 R4+R3R_4 + R_3R4+R3:
[101−4−40040−4200−14−1700−1−415190] \begin{bmatrix} 1 & 0 & 1 & -4 & -40 \\ 0 & 4 & 0 & -4 & 20 \\ 0 & -1 & 4 & -1 & 70 \\ 0 & -1 & -4 & 15 & 190 \end{bmatrix} 100004−1−1104−4−4−4−115−402070190 -
缩放第二行 14R2\frac{1}{4}R_241R2,并将第四行替换为 R4+R3R_4 + R_3R4+R3:
[101−4−40010−150−14−17000012270] \begin{bmatrix} 1 & 0 & 1 & -4 & -40 \\ 0 & 1 & 0 & -1 & 5 \\ 0 & -1 & 4 & -1 & 70 \\ 0 & 0 & 0 & 12 & 270 \end{bmatrix} 100001−101040−4−1−112−40570270 -
将第三行替换为 R3+R2R_3 + R_2R3+R2,缩放第四行 112R4\frac{1}{12}R_4121R4,并创建第四列的零:
[101050010027.50040120000122.5] \begin{bmatrix} 1 & 0 & 1 & 0 & 50 \\ 0 & 1 & 0 & 0 & 27.5 \\ 0 & 0 & 4 & 0 & 120 \\ 0 & 0 & 0 & 1 & 22.5 \end{bmatrix} 10000100104000015027.512022.5 -
缩放第三行 14R3\frac{1}{4}R_341R3,并将第一行替换为 R1−R3R_1 - R_3R1−R3:
[100020.0010027.5001030.0000122.5] \begin{bmatrix} 1 & 0 & 0 & 0 & 20.0 \\ 0 & 1 & 0 & 0 & 27.5 \\ 0 & 0 & 1 & 0 & 30.0 \\ 0 & 0 & 0 & 1 & 22.5 \end{bmatrix} 100001000010000120.027.530.022.5
结论:
解得:
T1=20.0,T2=27.5,T3=30.0,T4=22.5
T_1 = 20.0,\quad T_2 = 27.5,\quad T_3 = 30.0,\quad T_4 = 22.5
T1=20.0,T2=27.5,T3=30.0,T4=22.5
方程组的解为 (20.0,27.5,30.0,22.5)(20.0, 27.5, 30.0, 22.5)(20.0,27.5,30.0,22.5)。





















 3794
3794

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








