强化学习笔记(二)：有限马尔可夫决策过程(一)

有限马尔可夫决策过程

基本概念

多臂老虎机仅涉及评价性反馈，即动作的即时奖励，估计每个动作 $a$ 的价值 $q_{\ast }(a)$。

有限马尔可夫决策过程（Finite MDP）引入了关联性因素，即在不同状态（情境）下选择不同动作，动作不仅影响即时奖励，还通过改变环境状态影响未来的奖励，因此涉及延迟奖励以及长期与短期奖励之间的权衡。是强化学习中序贯决策问题的经典数学建模方式，扩展了多臂老虎机问题。在MDP中需要更精细的价值估计：

• 在状态 $ s $ 下动作 $ a $ 的最优价值：
  $$q_{\ast }(s,a)$$

• 状态 $ s $ 的最优价值（在最优策略下）：
  $$v_{\ast }(s)$$

这些状态相关的价值函数是将长期后果归因于具体动作选择的关键工具。

智能体-环境交互接口

实体	定义
智能体（Agent）	学习和决策的主体
环境（Environment）	智能体之外的一切，对动作做出响应

智能体选择动作，环境对这些动作做出响应，并向智能体呈现新的情境。环境还会产生奖励，智能体的目标就是通过选择动作，从长远来看最大化所获得的奖励总量。

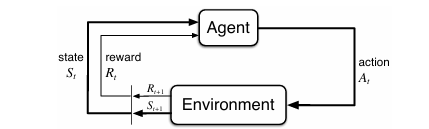
图3.1：马尔可夫决策过程中智能体与环境的交互。

交互流程

在离散的时间步$ t = 0, 1, 2, \dots $内，智能体与环境持续交互，每个时间步发生以下事件序列：
$$S_t\stackrel{\text{agent}}{\to }{A}_t\stackrel{\text{environment}}{\to }{R}_{t+1},S_{t+1}$$

即：

1. 智能体观察当前状态 $ S_t \in \mathcal{S} $
2. 选择动作 $ A_t \in \mathcal{A}(s) $
3. 环境响应：
   • 给出奖励 $ R_{t+1} \in \mathcal{R} \subset \mathbb{R} $
   • 进入新状态 $ S_{t+1} $

整个交互过程形成一个序列，称为轨迹：

$$S_0,A_0,R_1,S_1,A_1,R_2,S_2,A_2,R_3,\dots \text{\hspace{1em}(3.1)}$$

有限MDP

状态集 $ \mathcal{S} $、动作集 $ \mathcal{A} $、奖励集 $ \mathcal{R} $：有限个可能取值都只有有限个元素。

随机变量 $R_t$ 和 $S_t$ 具有明确定义的离散概率分布，且这些分布仅依赖于前一个状态和动作。

对于这些随机变量的特定取值 $s^{\prime }\in \mathcal{S}$ 和 $r\in \mathcal{R}$，在给定前一个状态 $s$ 和动作 $a$ 的条件下，它们在时间 $t$ 出现的概率为：
p(s′,r∣s,a)≐Pr⁡{ St=s′,Rt=r∣St−1=s,At−1=a}(3.2) p(s', r | s, a) \doteq \Pr\{S_t = s', R_t = r \mid S_{t-1} = s, A_{t-1} = a\} \tag{3.2} p(s′,r∣s,a)≐Pr{ St​=s′,Rt​=r∣St−1​=s,At−1​=a}(3.2)

[!NOTE]

符号 $ \doteq $ 表示“定义为”

同时有

$$\sum _{s^{\prime }\in \mathcal{S}}\sum _{r\in \mathcal{R}}p(s^{\prime },r|s,a)=1,\forall s\in \mathcal{S},a\in \mathcal{A}(s)\text{\hspace{1em}(3.3)}$$

在马尔可夫决策过程中，条件概率 $ p(s’, r|s, a) $ 决定了所有未来动态。$ S_t $ 和 $ R_t $ 的分布仅依赖于前一状态 $ S_{t-1} $ 和动作 $ A_{t-1} $，与更早的历史无关。这要求状态必须包含所有对未来有影响的信息。马尔可夫性质是对“状态”的限制，而非过程本身；若状态满足此性质，则称其具有马尔可夫性。

相关计算量

状态转移概率

p(s′∣s,a)≐Pr⁡{ St=s′∣St−1=s,At−1=a}=∑r∈Rp(s′,r∣s,a)(3.4) p(s'|s,a) \doteq \Pr\{S_t = s' \mid S_{t-1} = s