机蒜客第六章：Fib数列问题之二-优快云博客

本文介绍了一种使用矩阵快速幂算法解决Fib数列问题的方法，通过定义特定的矩阵进行乘法运算，实现对Fib数列的高效计算。代码中详细展示了矩阵乘法、矩阵快速幂和单位矩阵的定义，适用于处理大规模Fib数列计算任务。

机蒜客练习题：Fib数列问题之二

题目

在这里插入图片描述

样例

在这里插入图片描述

思路

模板题，课程内已细致讲解，不再赘述。
在这里插入图片描述
计算公式：

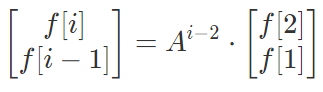
代码

#include<iostream>
using namespace std;
struct matrix
{
   long long a[100][100];
};
matrix matrix_mul(matrix A, matrix B, int mod) {
    // 2 个矩阵相乘
    matrix C;
    for (int i = 0; i <2; ++i) {
        for (int j = 0; j < 2; ++j) {
            C.a[i][j] = 0;
            for (int k = 0; k < 2; ++k) {
                C.a[i][j] += A.a[i][k] * B.a[k][j] % mod;
                C.a[i][j] %= mod;
            }
        }
    }
    return C;
}
matrix unit() {
    // 返回一个单位矩阵
    matrix res;
    for (int i = 0; i < 2; ++i) {
        for (int j = 0; j < 2; ++j) {
            if (i == j) {
                res.a[i][j] = 1;
            } else {
                res.a[i][j] = 0;
            }
        }
    }
    return res;
}
matrix matrix_pow(matrix A, long long i, long long mod) {
    // 快速求矩阵 A 的 n 次方
    matrix res = unit(), temp = A;
    for (; i; i /= 2) {
        if (i & 1) {
            res = matrix_mul(res, temp, mod);
        }
        temp = matrix_mul(temp, temp, mod);
    }
    return res;
}
int main()
{
    long long m,i;
    cin>>i>>m;
    if(i==1){cout<<"1";return 0;}
    if(i==2){cout<<"1";return 0;}
    if(i==3){cout<<"2";return 0;}
    matrix f,f0,fff;
    f.a[0][0]=1;
    f.a[0][1]=1;
    f.a[1][0]=1;
    f.a[1][1]=0;
    f0.a[0][0]=1;
    f0.a[0][1]=0;
    f0.a[1][0]=1;
    f0.a[1][1]=0;
    fff=matrix_mul(matrix_pow(f,i-2,m),f0,m);
    cout<<fff.a[0][0]+fff.a[0][1];
    return 0;
}