趣题：用最少的点挡住所有可能的反射路径

   有一个正方形的房间，房间的四壁都是镜子。房间里有一个天使和一个恶魔。假设房间是一个单位正方形 [0, 1] × [0, 1] ，那么天使和恶魔便是这个正方形内的两个点 (a, b) 和 (c, d) 。恶魔想要在原地发射致命激光杀死天使(激光可以无限地在镜子间反射)。天使可以根据恶魔的位置，预先在房间里放置一些守卫为他挡住激光(守卫实际上也是一些点)。当然，天使可以在自己周围密密麻麻地放一圈守卫，围成一个封闭的圆形，从而让恶魔不管朝什么方向发射激光，最终都无法击中天使。我们的问题是，能把守卫的数量减少到可数个点吗？能把守卫的数量减少到有限个点吗？

     这是一个非常经典的问题，我已经见过不止一次了。它可以重新叙述为很多更有趣的实际问题。去年的这个时候，网友 Spark 发来邮件，分享了他在看台球比赛时想到的一个问题：最少需要摆放多少个球，才能挡住白球到目标球的所有可能的路线，迫使对手犯规？如果我们把台球也抽象成一个一个的点，问题就和前面提到的情况一样了。

     今天，我终于看到了这个问题的答案，颇为激动，在此和大家分享。

           

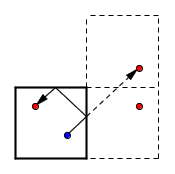
     解决这类问题的一个常用技巧便是利用多次翻折把反射路线变为直线。现在，把这个房间不断地翻折，让它平铺整个平面；各种复杂的反射路径，就变成了一条一条的直线段。这样，我们便可认为恶魔的激光并不是在反射，而是径直穿过镜面射入房间的“虚像”。恶魔的目标，便是直接对准某个天使的虚像射击。由于天使的虚像只有可数个，因此天使可以在恶魔周围摆放可数个守卫，一一挡住射向每一个天使虚像的激光(有觉得下图中的网格线弯曲得异常严重吗？那是你的错觉)。

    

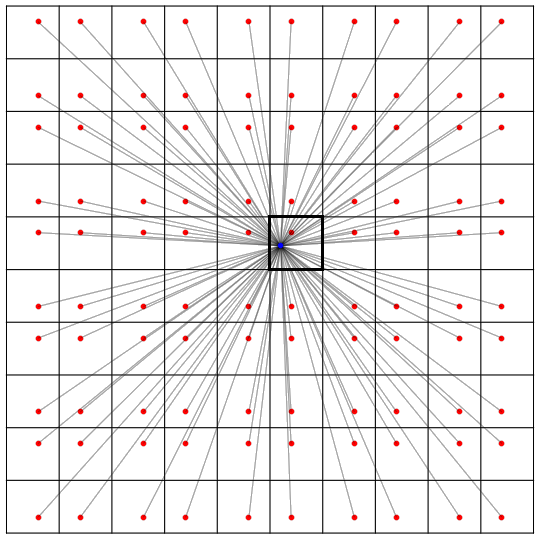
     守卫的数量还能进一步减少到有限个点吗？注意到，即使只有有限的守卫，经过翻折之后也将会产生无穷多个守卫的虚像，每一个虚像都可以帮忙挡住激光。因此，只使用有限的守卫是完全有可能的。事实上，不管天使的位置 (a, b) 和恶魔的位置 (c, d) 在哪儿，摆放 16 个守卫总是足够的。下面我们给出一个具体的方案。

     容易看出，所有天使虚像的坐标都形如 (2m ± a, 2n ± b) ，其中 m 和 n 都是整数(可能为负)。我们先来考察其中一类虚像，即所有形如 (2m - a, 2n + b) 的点。对于任意确定的 m 和 n ，恶魔 (c, d) 和天使虚像 (2m - a, 2n + b) 的连线都会经过 (m - a/2 + c/2, n + b/2 + d/2) 这个点，因为这个点其实是前两个点的连线的中点。也就是说，在每个格子里的 (- a/2 + c/2, b/2 + d/2) 处都放一个点，就能够挡住所有射向这类虚像的激光了：

    

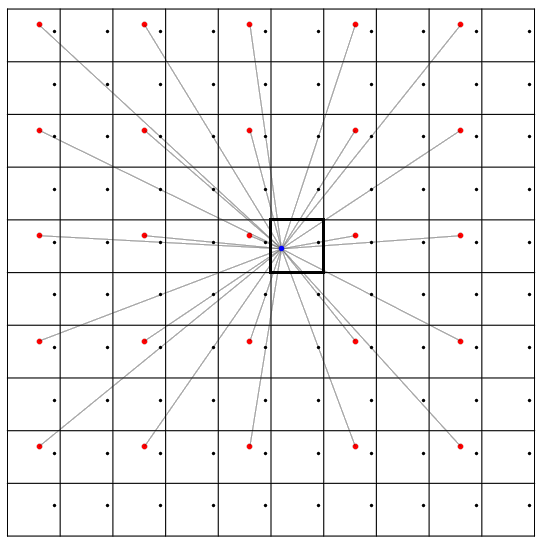
     等等，等等，这些黑点都是从哪儿来的？别忘了，我们只能通过翻折建立虚像，不能通过平移建立虚像。因此，事实上，我们需要在初始的房间里对称地放置四个守卫，才能让所有“虚房间”的 (- a/2 + c/2, b/2 + d/2) 处都有一个点：

    

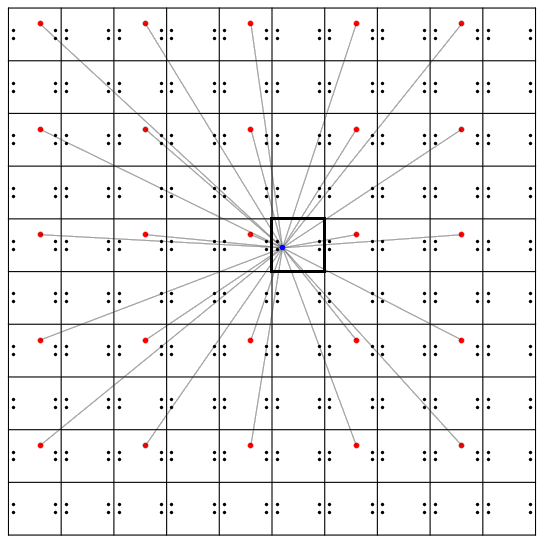
     类似地，天使的虚像坐标还有 (2m + a, 2n + b) 、 (2m + a, 2n - b) 、 (2m - a, 2n - b) 三类，它们又需要另外四组守卫。因此，总共 16 个守卫便能挡住所有可能的激光。这 16 个守卫的位置分别是 (a/2 ± c/2, b/2 ± d/2) 、 (a/2 ± c/2, 1 - (b/2 ± d/2)) 、 (1 - (a/2 ± c/2), b/2 ± d/2) 、 (1 - (a/2 ± c/2), 1 - (b/2 ± d/2)) 。