图论基础与算法详解-优快云博客

本文链接：https://blog.youkuaiyun.com/sheldonwong/article/details/83008636

本文深入探讨了图论的基本概念，包括图的定义、分类和特性，详细讲解了图的存储方式，如邻接矩阵和邻接表，并对比了它们在稀疏图和稠密图中的适用性。此外，文章还介绍了图的遍历算法，深度优先遍历和广度优先遍历，以及常见算法如Floodfill和最短路径算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 图

图是由点和变构成的

图的分类

无向图

有向图

无权图

有权图

稀疏图

稠密图

图的连通性：连通分量

简单图：没有平行边和自环边

2. 图的存储

邻接矩阵

无向图

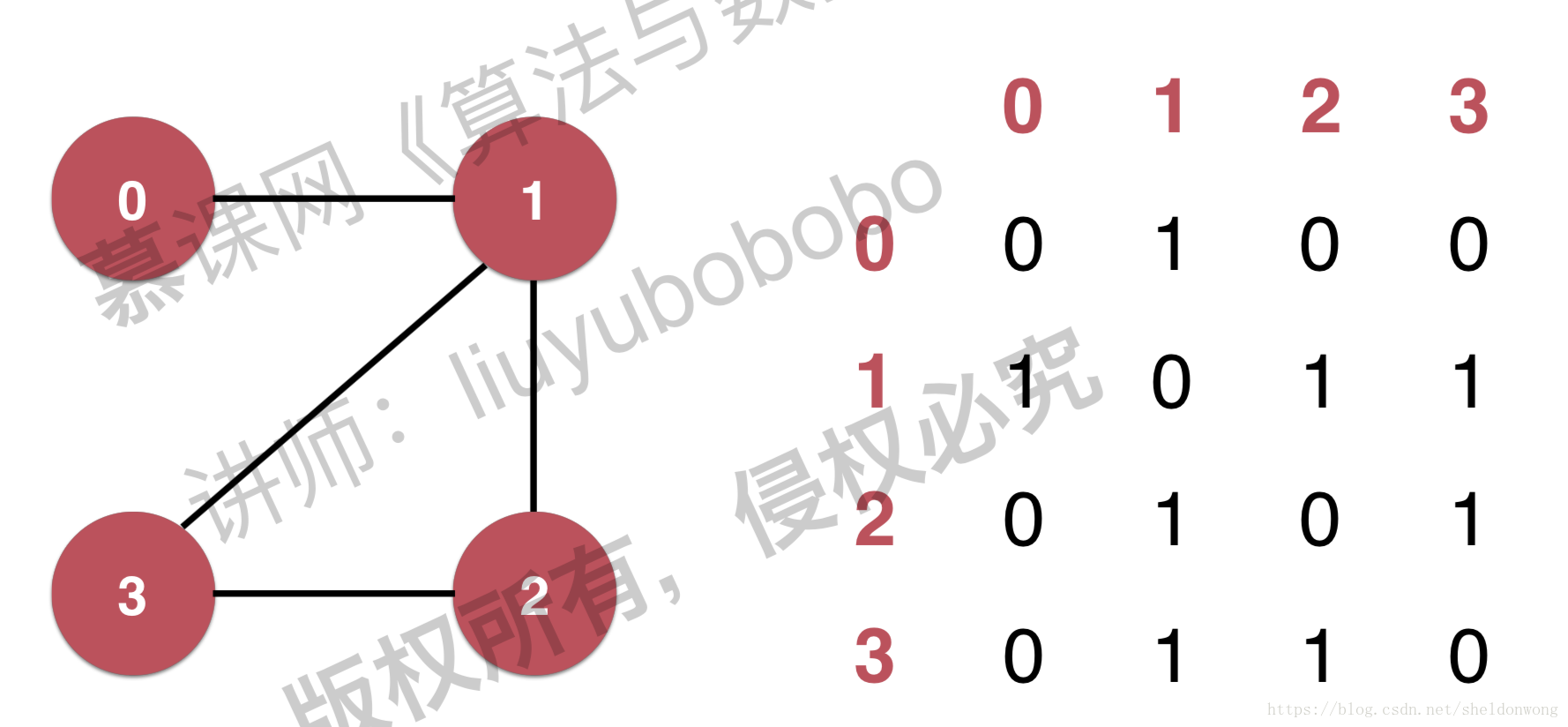
有向图

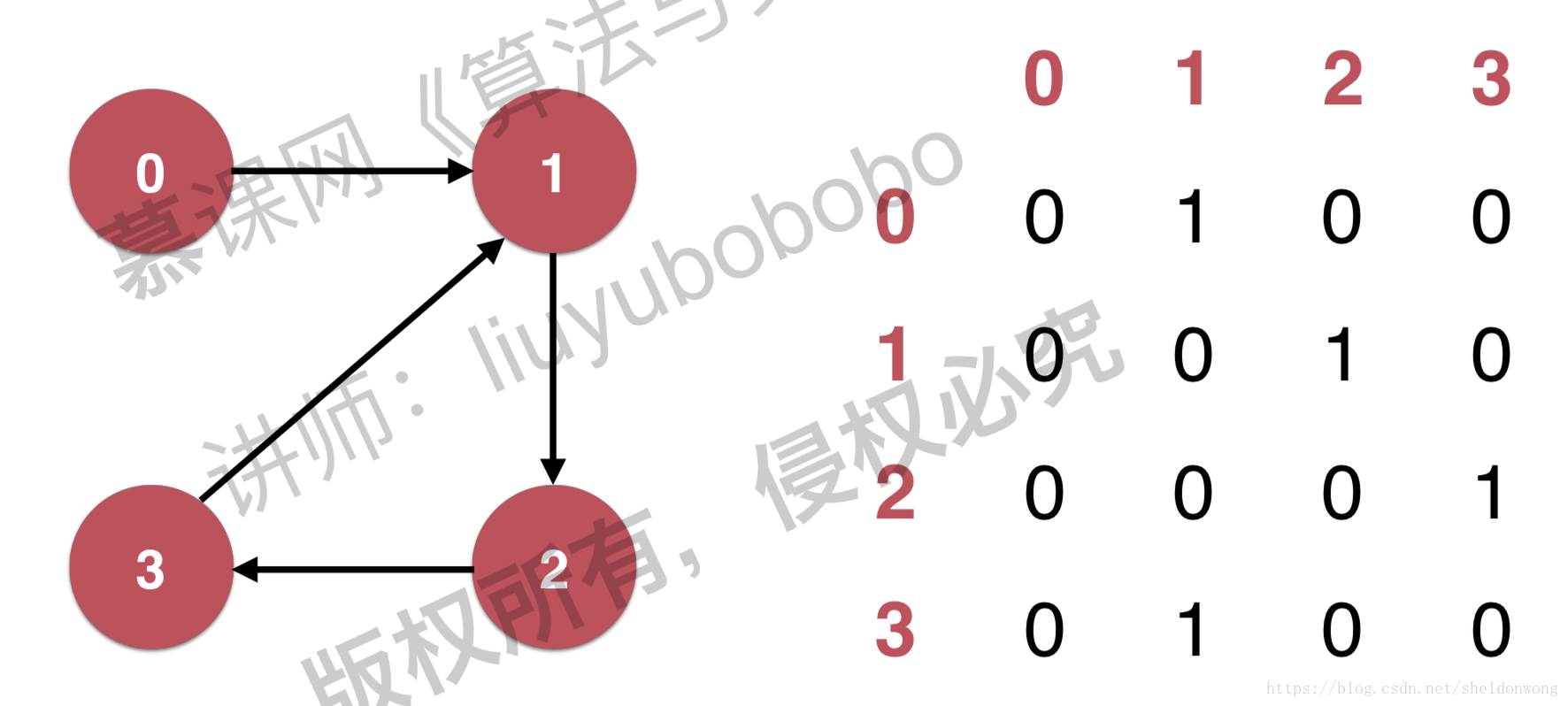
邻接表

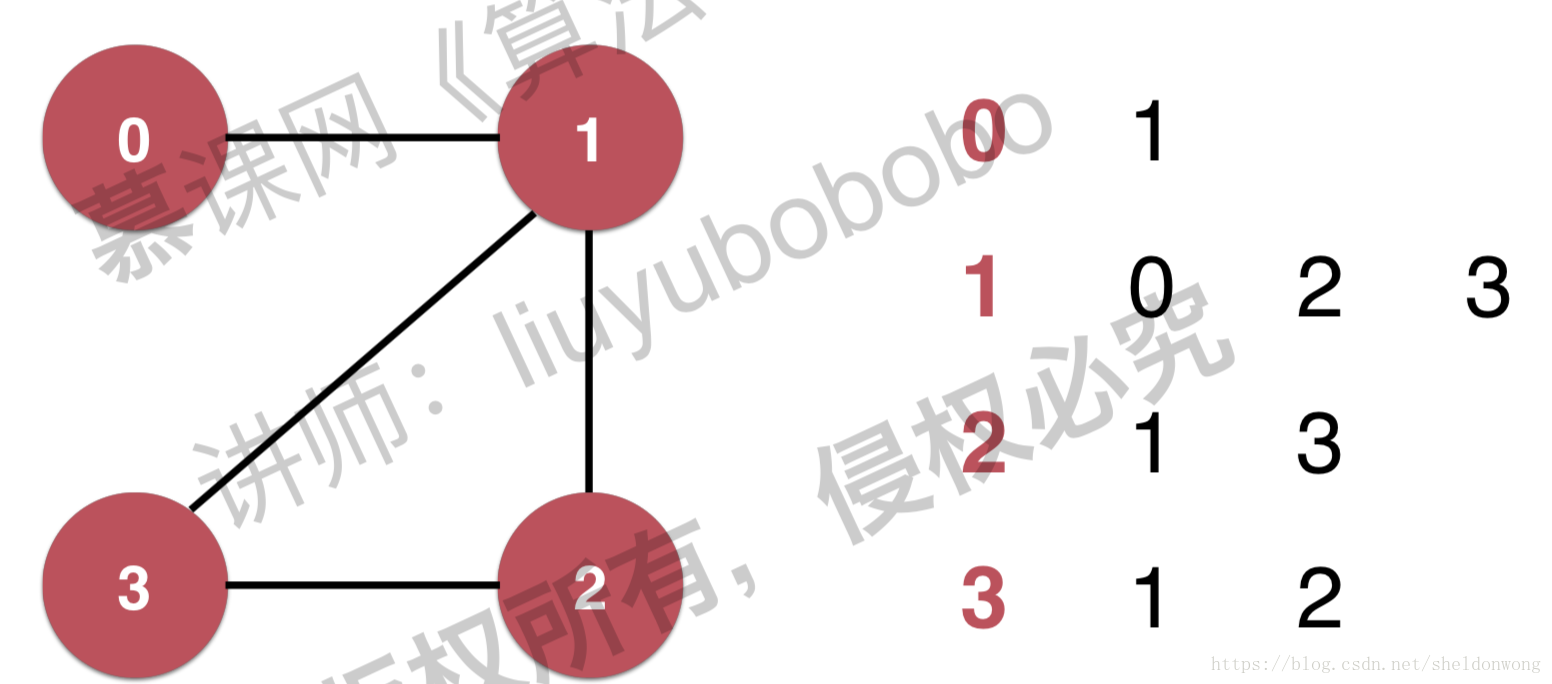
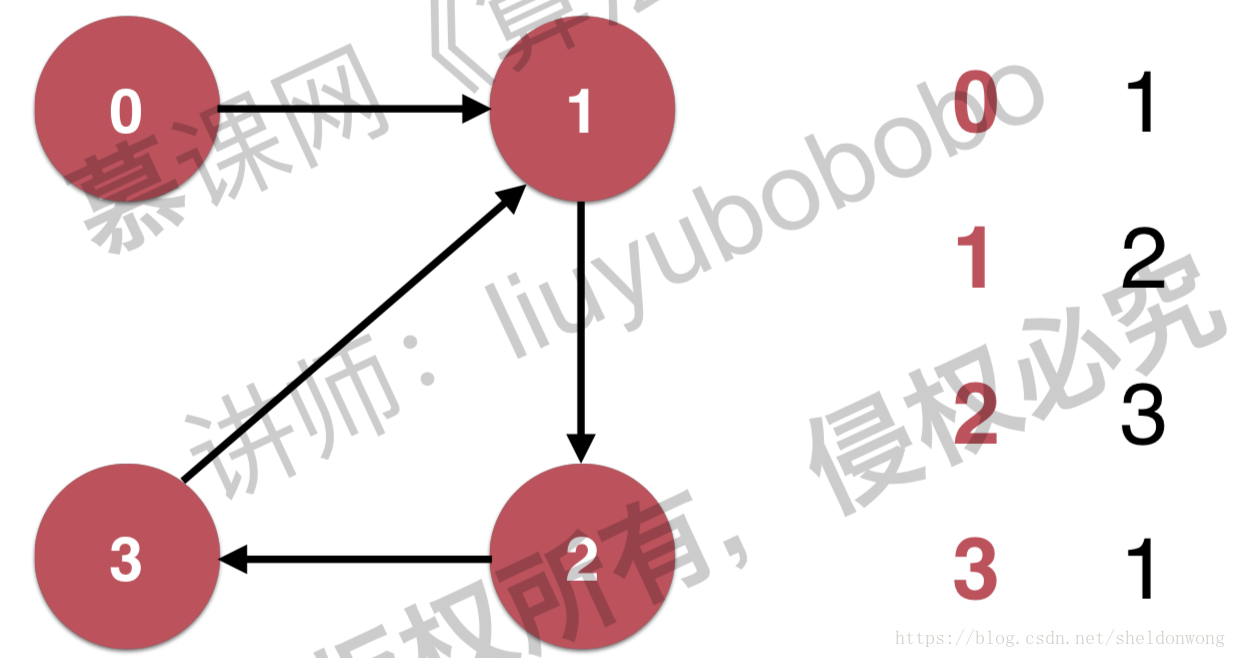
如何将一个图转换成计算机课存储的方式？

1. 把节点列表列出来

2. 在邻接表中填邻接节点（在邻接矩阵中填充邻接矩阵）

邻接表适合表示稀疏图，邻接矩阵适合表示稠密图

3. 图的遍历（搜索）

3.1 深度优先遍历

# 用邻接表表示图
graph = {
	'A':['B','C'],
	'B':['A','C','D'],
	'C':['A','B','D','E'],
	'D':['B','C','E','F'],
	'E':['C','D'],
	'F':['D']
}

# 深度优先搜索
def DFS(graph,start):
	stack = []
	stack.append(start)

	seen = set()
	seen.add(start)

	while(len(stack) > 0):
		vertex = stack.pop()
		neighbor_nodes = graph[vertex]

		for w in neighbor_nodes:
			if w not in seen:
				stack.append(w)
				seen.add(w)
		print(vertex)

时间复杂度：

稀疏图：O(V+E)

稠密图：O(V^2)

3.2 广度优先遍历


# 用邻接表表示图
graph = {
	'A':['B','C'],
	'B':['A','C','D'],
	'C':['A','B','D','E'],
	'D':['B','C','E','F'],
	'E':['C','D'],
	'F':['D']
}

# 广度优先搜索
def BFS(graph,start):
	queue = []
	queue.append(start)

	seen = set()
	seen.add(start)

	while(len(queue) > 0):
		vertex = queue.pop(0)
		neighbor_nodes = graph[vertex]

		for w in neighbor_nodes:
			if w not in seen:
				queue.append(w)
				seen.add(w)
		print(vertex)

BFS(graph, 'A')

时间复杂度：

稀疏图：O(V+E)

稠密图：O(V^2)