力扣经典题解：LRU缓存机制（146. LRU Cache）数据结构设计艺术

最新推荐文章于 2025-12-15 23:25:39 发布

原创最新推荐文章于 2025-12-15 23:25:39 发布 · 737 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #缓存 #数据结构

题目描述

设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

要实现 LRUCache 类：

LRUCache(int capacity) 初始化 LRU 缓存
int get(int key) 若 key 存在返回对应值，否则返回 -1
void put(int key, int value) 若 key 存在更新值，不存在则插入。若缓存满则删除最久未使用的项

要求：get 和 put 操作时间复杂度均为 O(1)

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

解题思路

数据结构选择

要实现 O(1) 的 get 和 put 操作，需要两种数据结构协作：

哈希表：提供 O(1) 时间的键值查找
双向链表：维护访问顺序（最近访问的节点在头部，最久未访问的在尾部）

为什么是双向链表？

单链表删除节点需要遍历查找前驱节点
双向链表可以直接获取前后节点，删除效率 O(1)
移动节点操作更高效（先删除后插入头部）

算法设计图解

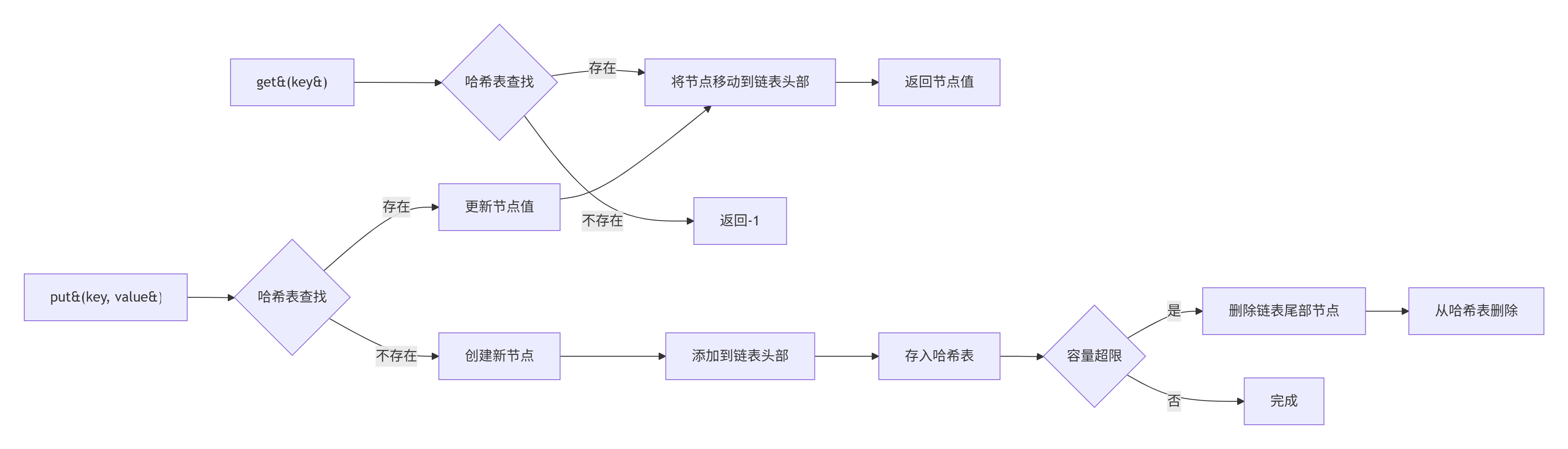
Java实现

import java.util.HashMap;
import java.util.Map;

class DLinkedNode {
    int key;
    int value;
    DLinkedNode prev;
    DLinkedNode next;
    
    public DLinkedNode() {}
    
    public DLinkedNode(int key, int value) {
        this.key = key;
        this.value = value;
    }
}

public class LRUCache {
    private Map cache = new HashMap<>();
    private int size;       // 当前缓存数量
    private int capacity;   // 缓存容量
    private DLinkedNode head, tail; // 双向链表的头尾虚节点

    public LRUCache(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        // 使用伪头节点和伪尾节点简化操作
        head = new DLinkedNode();
        tail = new DLinkedNode();
        head.next = tail;
        tail.prev = head;
    }

    public int get(int key) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        // 访问节点后移动到链表头部
        moveToHead(node);
        return node.value;
    }

    public void put(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            // 新建节点
            DLinkedNode newNode = new DLinkedNode(key, value);
            // 添加进哈希表
            cache.put(key, newNode);
            // 添加到双向链表头部
            addToHead(newNode);
            size++;
            if (size > capacity) {
                // 删除链表尾部节点
                DLinkedNode tailNode = removeTail();
                // 从哈希表中删除
                cache.remove(tailNode.key);
                size--;
            }
        } else {
            // 更新值并移动到头部
            node.value = value;
            moveToHead(node);
        }
    }

    // 辅助方法：添加节点到头部
    private void addToHead(DLinkedNode node) {
        node.prev = head;
        node.next = head.next;
        head.next.prev = node;
        head.next = node;
    }

    // 辅助方法：删除节点
    private void removeNode(DLinkedNode node) {
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }

    // 辅助方法：移动节点到头部
    private void moveToHead(DLinkedNode node) {
        removeNode(node);
        addToHead(node);
    }

    // 辅助方法：移除尾部节点
    private DLinkedNode removeTail() {
        DLinkedNode tailNode = tail.prev;
        removeNode(tailNode);
        return tailNode;
    }
}