队列与循环队列

最新推荐文章于 2025-03-23 10:12:45 发布
最新推荐文章于 2025-03-23 10:12:45 发布
阅读量278 收藏 6
点赞数 9
CC 4.0 BY-SA版权
分类专栏： 数据结构 文章标签： 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/sdmdnf/article/details/134434960
本文主要介绍了队列与循环队列。队列是“先进先出”的线性表，使用链表创建，包含初始化、入队、出队等操作。循环队列则是为解决顺序队列“假溢出”问题出现，通过将存储空间视为环形结构，利用顺序表创建，有判空、判满、入队、出队等操作。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

队列与循环队列

队列的定义

队列（Queue）是一种==“先进先出”==（First In First Out，FIFO）的线性表，只能允许队头出，队尾进。与现实生活中的排队类似。只能允许队头的人出去，不允许插队，因此想要排队就要从队尾排。

024AC2F0

与栈（stack)不同的“先进后出”，即只运行在栈顶进行操作，不允许在栈底操作。类似于弹夹，先发射最上面那颗子弹（先进后出）

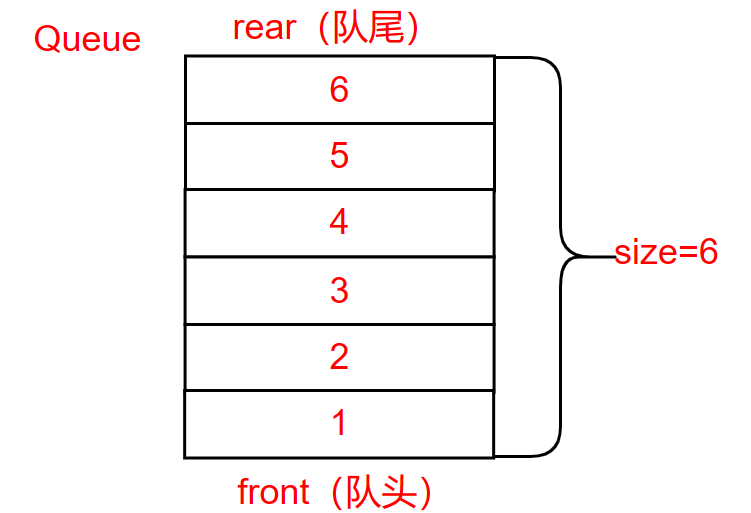
image-20231114184425952

入队列的顺序：1->2->3->4->5->6

出队列的顺序：1->2->3->4->5->6

队列的创建

根据数据结构的知识，我们知道定义线性表有两种结构

顺序表：是在计算机内存中以数组的形式保存的线性表，是指用一组地址连续的存储单元依次存储数据元素的线性结构，使得线性表中在逻辑结构上相邻的数据元素存储在相邻的物理存储单元中，即通过数据元素物理存储的相邻关系来反映数据元素之间逻辑上的相邻关系

链表：一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针

由于顺序表在队列中并不多用，这里我使用链表的方式来创建队列，至于这两个结构创建的队列有什么区别，可以自行百度

创建队列

队列

typedef struct Queue
{
	QNode* front;//队头
	QNode* rear;//队尾
	int size;//队列大小
}Queue;

创建保存队列内容的节点

typedef int QDataType;
typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

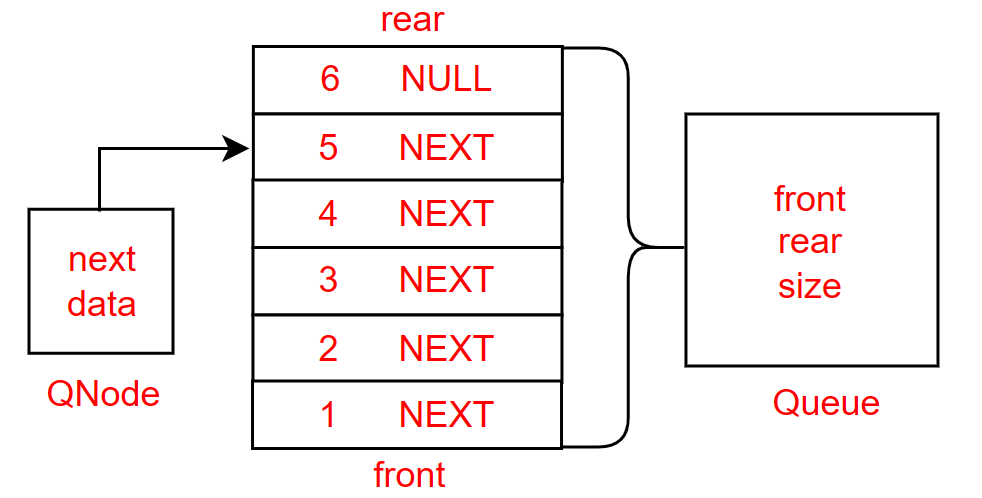
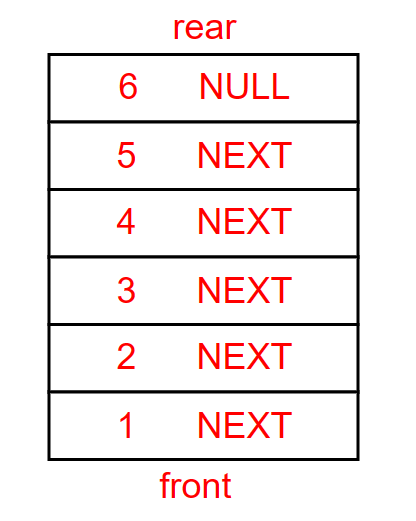
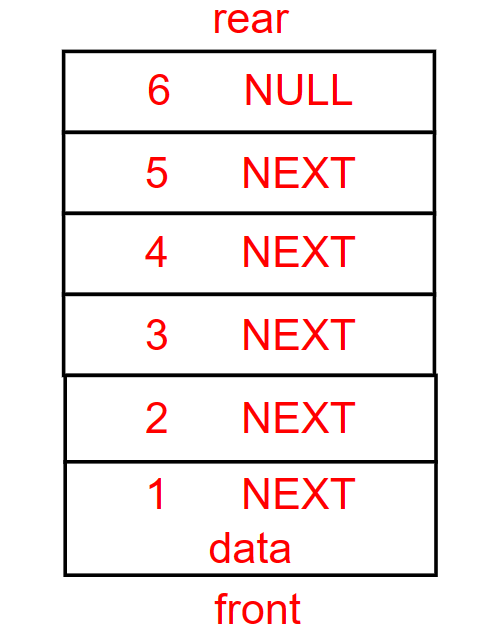
图解

image-20231114190003249

队列的初始化

初始化很简单，就是一切从0开始嘛，这里可以断言(assert)来检查指针是否正确

//初始化队列
void QueueInit(Queue* q) {
	assert(q);
	//置空
	q->front = q->rear = NULL;
	q->size = 0;
}
队列的入队

024B4167

向内存申请一个节点的空间，用队列的尾指针（rear）尾插这些创建的节点

注意：刚开始rear跟front都是指向NULL，因此要判断没有节点时，rear直接指向新节点，随后就是普普通通的尾插了

// 队尾入队列
void QueuePush(Queue* q, QDataType data) {
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL) {
		exit(-1);
	}

	//插入
	//1.插入数据
	newnode->data = data;
	newnode->next = NULL;
	//2.没有节点时
	if (q->rear == NULL) {
		q->front = q->rear = newnod	e;
	}
	else {
		//尾插
		q->rear->next = newnode;
		//更新尾结点
		q->rear = newnode;
	}
	//更新队列大小
	q->size++;
}

图解

push->1,push->2,push->3,push->4,push->5,push->6

image-20231115000517164

最后

image-20231115000652882

判断队列是否为空

这里的返回值是布尔值（true or false)，需要引#include<stdbool.h>头文件

可以看成if(q->front==NULL)时return true否则就return false

也要断言一下

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
bool QueueEmpty(Queue* q) {
	assert(q);
	return q->front == NULL;
}
获取队列中有效元素个数

在push时，已经让size++了，因此直接返回size就OK了

依旧断言一下

// 获取队列中有效元素个数
int QueueSize(Queue* q) {
	assert(q);
	return q->size;
}
获取头队列元素

获取前判断指针是否不为空，队列是否为空

返回头节点（队头）的数据即可

// 获取队列头部元素
QDataType QueueFront(Queue* q) {
	assert(q);
	assert(!QueueEmpty(q));
	return q->front->data;
}

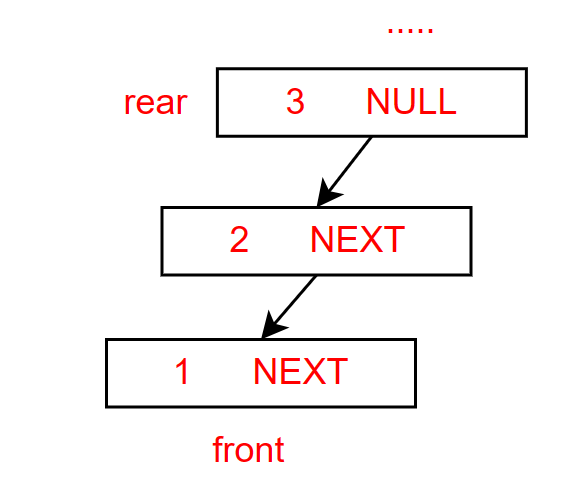
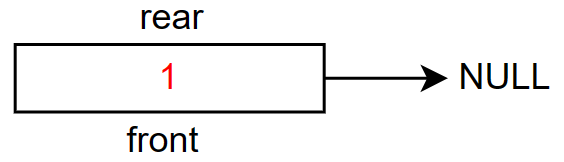
图解

image-20231115103215152

这里也就是返回1

获取队尾元素

跟获取队头元素一样

// 获取队列队尾元素
QDataType QueueBack(Queue* q) {
	assert(q);
	assert(!QueueEmpty(q));
	return q->rear->data;
}
队列的出队

024B6683

首先要断言，队列为空时，就不能出队了

这里有两种情况

1.当只有只有一个节点时

image-20231115104024890

2.当有多个节点时

image-20231115104433283

// 队头出队列
void QueuePop(Queue* q) {
	assert(q);
	//判断队是否空
	assert(!QueueEmpty(q));
	//1.只有一个元素时
	if (q->front->next == NULL) {
		free(q->front);
		q->rear = q->front = NULL;
	}
	//2.多个节点
	else {
		QNode* next = q->front->next;
		free(q->front);
		q->front = next;
	}

	q->size--;
}
队列的销毁

跟单链表的销毁一样

用一个指针遍历节点一个个删除，删除完后把front跟rear指针置空，把size归零

// 销毁队列
void QueueDestroy(Queue* q) {
	assert(q);
	//记录队头地址
	QNode* cur = q->front;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	//置空队头跟队尾指针
	q->front = q->rear = NULL;
	q->size = 0;
}

源代码

Queue.h
#pragma once
#pragma warning (disable:4996)
#include<stdio.h>
#include<malloc.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

// 队列的结构 指针集，通过这个可以访问QNode
typedef struct Queue
{
	QNode* front;
	QNode* rear;
	int size;
}Queue;

// 初始化队列
void QueueInit(Queue* q);
// 队尾入队列
void QueuePush(Queue* q, QDataType data);
// 队头出队列
void QueuePop(Queue* q);
// 获取队列头部元素
QDataType QueueFront(Queue* q);
// 获取队列队尾元素
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数
int QueueSize(Queue* q);
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
bool QueueEmpty(Queue* q);
// 销毁队列
void QueueDestroy(Queue* q);

Queue.c
#include "Queue.h"
//初始化队列
void QueueInit(Queue* q) {
	assert(q);
	//置空
	q->front = q->rear = NULL;
	q->size = 0;
}

// 销毁队列
void QueueDestroy(Queue* q) {
	assert(q);
	//记录队头地址
	QNode* cur = q->front;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	//置空队头跟队尾指针
	q->front = q->rear = NULL;
	q->size = 0;
}

// 队尾入队列
void QueuePush(Queue* q, QDataType data) {
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL) {
		exit(-1);
	}

	//插入
	//1.插入数据
	newnode->data = data;
	newnode->next = NULL;
	//2.没有节点时
	if (q->rear == NULL) {
		q->front = q->rear = newnode;
	}
	else {
		//尾插
		q->rear->next = newnode;
		//更新尾结点
		q->rear = newnode;
	}
	//更新队列大小
	q->size++;
}

// 队头出队列
void QueuePop(Queue* q) {
	assert(q);
	//判断队是否空
	assert(!QueueEmpty(q));
	//1.只有一个元素时
	if (q->front->next == NULL) {
		free(q->front);
		q->rear = q->front = NULL;
	}

	else {
		QNode* next = q->front->next;
		free(q->front);
		q->front = next;
	}

	q->size--;
}

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0
bool QueueEmpty(Queue* q) {
	assert(q);
	return q->front == NULL;
}

// 获取队列中有效元素个数
int QueueSize(Queue* q) {
	assert(q);
	return q->size;
}

// 获取队列头部元素
QDataType QueueFront(Queue* q) {
	assert(q);
	assert(!QueueEmpty(q));
	return q->front->data;
}

// 获取队列队尾元素
QDataType QueueBack(Queue* q) {
	assert(q);
	assert(!QueueEmpty(q));
	return q->rear->data;
}

Test.c
#include "Queue.h"

void test1() {
	Queue pq;
	QueueInit(&pq);
	QueuePush(&pq, 1);
	QueuePush(&pq, 2);
	QueuePush(&pq, 3);
	QueuePush(&pq, 4);
	QueuePush(&pq, 5);
}

int main() {
	test1();

	return 0;
}

循环队列

image-20231115110824084

在介绍循环队列之前，先来解释一个概念

024BE8A3

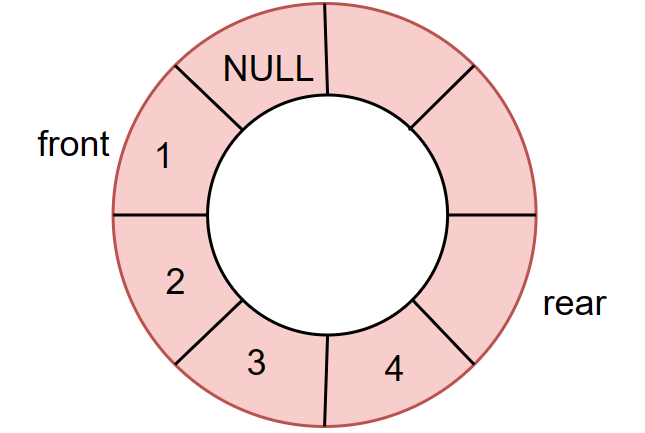
在顺序队列中，当尾指针移动到队列的边界时，即使队列前面的存储空间是空的，也会发生溢出，这种情况被称为“假溢出”

因此为了解决"假溢出"问题，充分利用内存空间，循环队列就出现了

循环队列通过将队列的存储空间视为一个循环的环形结构，使得队列的尾指针可以绕回到队列的头部继续存储数据，从而充分利用存储空间，避免了"假溢出"问题的发生。同时，循环队列的操作也相对简单，入队和出队操作都可以在固定的时间内完成，具有较高的效率

这里通过622. 设计循环队列 - 力扣（LeetCode）上的题目来讲解

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

  • MyCircularQueue(k): 构造器，设置队列长度为 k 。
  • Front: 从队首获取元素。如果队列为空，返回 -1 。
  • Rear: 获取队尾元素。如果队列为空，返回 -1 。
  • enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
  • deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
  • isEmpty(): 检查循环队列是否为空。
  • isFull(): 检查循环队列是否已满。

示例：

MyCircularQueue circularQueue = new MyCircularQueue(3); // 设置长度为 3
circularQueue.enQueue(1);  // 返回 true
circularQueue.enQueue(2);  // 返回 true
circularQueue.enQueue(3);  // 返回 true
circularQueue.enQueue(4);  // 返回 false，队列已满
circularQueue.Rear();  // 返回 3
circularQueue.isFull();  // 返回 true
circularQueue.deQueue();  // 返回 true
circularQueue.enQueue(4);  // 返回 true
circularQueue.Rear();  // 返回 4

提示：

  • 所有的值都在 0 至 1000 的范围内；
  • 操作数将在 1 至 1000 的范围内；
  • 请不要使用内置的队列库。

看题目要求设计一个循环队列，且不能使用内置的队列库，也就是让我们造轮子嘛

构造循环队列

024C375F

跟队列一样，构造时有两个结构可以选择

1.顺序表

2.链表

根据分析，创建循环队列用顺序表是最佳选择，为了更好的判断队列是否为空或者为满（与队列的有效元素有关），题目要求：Rear: 获取队尾元素。如果队列为空，返回 -1 。如果使用链表，front跟rear在节点中循环是很方便的，但是返回rear节点时，由于队列的有效范围是[front,rear),因此rear指针需要返回上一个节点才是真正的队尾，双向循环链表可以解决这个问题，结构过于复杂。而顺序表的rear直接返回上一个位置即可，非常方便。

typedef struct {
    int *a;
    int rear;
    int front;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue *obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    //开k+1个空间
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->rear=obj->front=0;
    obj->k=k;
    return obj;
}

循环队列的判空

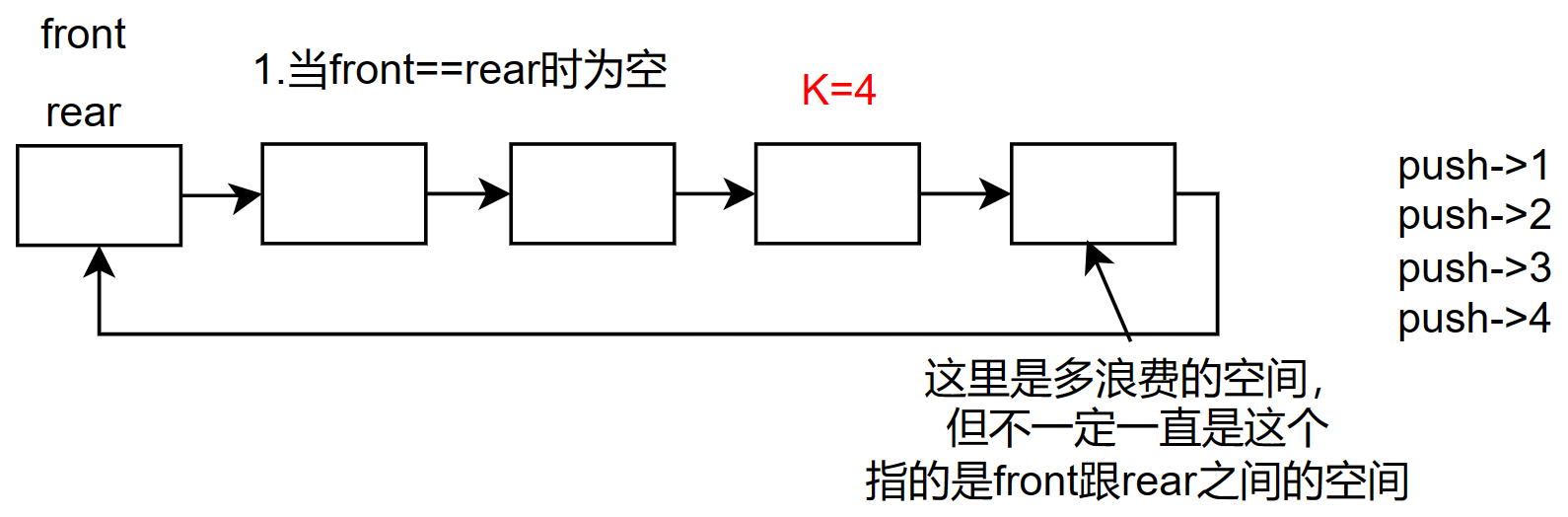
判空很简单，front==rear时队列为空。

为了更直观观察循环队列的结果，我将环简化成以下结构

image-20231115194230997

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    //重合时为空
    return obj->rear==obj->front;
}

循环队列的判满

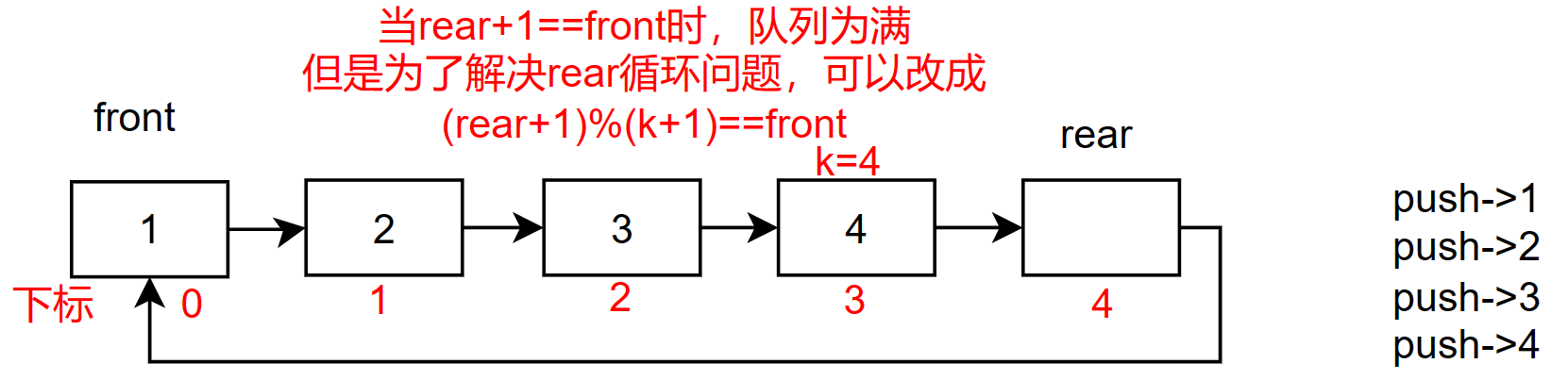
当队列是满的时，根据循环队列的特点，就是rear的下一个位置是front就是满了，以下图为例

1.rear的下一个rear+1=5，咋一看rear怎么越界了？不是说好的rear的下一个是front吗？

为了解决这个问题，可以将rear+1的结果%(k+1)防止越界，同时也解决了一个大问题，当rear走到队列下标最大的地方时，对(k+1)求余，结果就是0。这个结论很重要，是循环队列的核心，请同学们时刻记住

image-20231115195002149

2.当pop->1,pop->2,pop->3时，如下图

image-20231115200702506

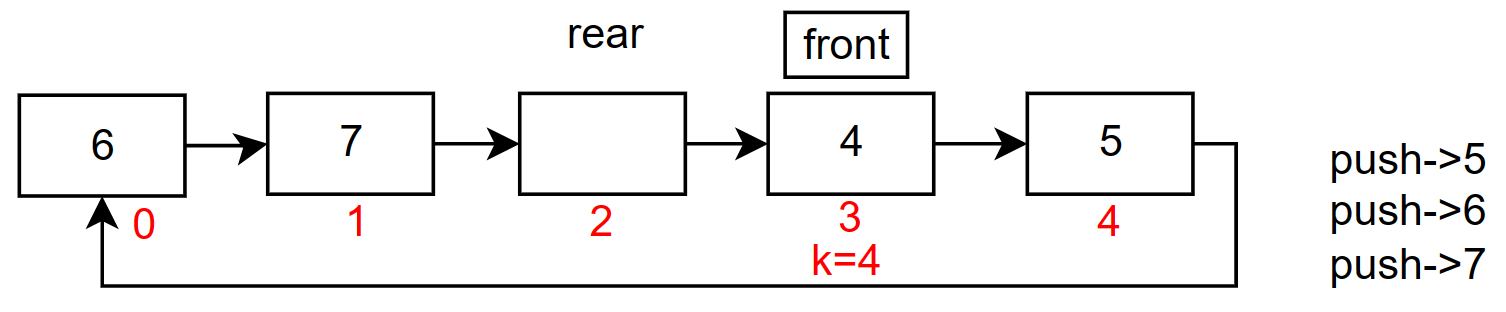
然后再push->5,push->6,push->7，如下图

image-20231115201333153

此时是第二种队列满的情况

把下标套进上面的结论(rear+1)%(K+1)==front，(2+1)%(4+1)==3刚好就是3,无论是在那个地方队列满了，这个结论都可以完美解决这个问题（发明这个的一定是个天才）

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    //rear的下一个是front时为满
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

循环队列的入队

024D0DDA

同样，入队列之前先要判满

满了就返回false，插入成功就返回true（题目要求）

先插入value在让rear++才符合范围[front,rear)

因为是顺序表，rear指针如何返回到下标为0的地方是个大问题，还记得上面的结论吗，直接套进去rear的下标会发现，rear到下标最大的位置后，对k+1取余，就可以回到下标为0的位置（对k+1取余的本质就是限制rear在这个范围内移动，解决越界的问题）

因此，更新rear可每次对k+1取余

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    //入队列
    //先判满
    if(myCircularQueueIsFull(obj))
        return false;
    
    obj->a[obj->rear]=value;
    obj->rear++;
    //更新rear
    obj->rear %= obj->k+1;

    return true;
}

循环队列的出队

出队跟入队类似，出去之前判空。

同样，上面那个结论可以用于front的更新

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    //出队列
    ++obj->front;
    //更新front
    obj->front %= obj->k+1;
    return true;
}

返回循环队列的队头

为空返回-1，不为空直接返回front即可

int myCircularQueueFront(MyCircularQueue* obj) {
   if(myCircularQueueIsEmpty(obj))
        return -1;
    else
         return obj->a[obj->front];
}

返回循环队列的队尾

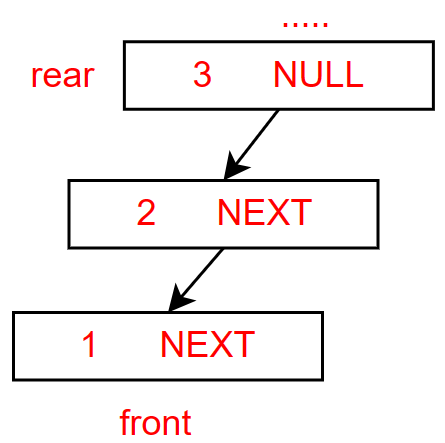
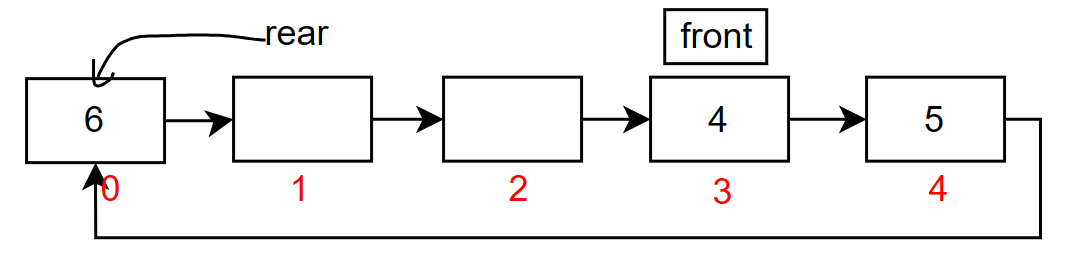
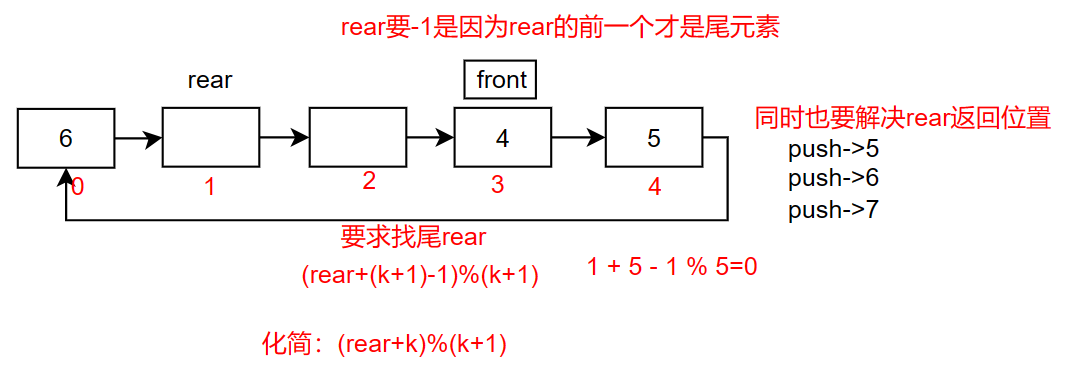
以下图为例

image-20231115204455055

获取队尾元素，就要将rear返回上一个位置

这又涉及到另一个结论(rear-1+(k+1))%(k+1)，化简后(rear+k)%(k+1)

这个结论可以直接背下来，不理解的可以看下图，把rear下标直接代进去

image-20231116093922426

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->rear+obj->k)%(obj->k+1)]; 
}

循环队列的删除

用顺序表开了两个空间，删除时直接free即可

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

源代码

typedef struct {
    int *a;
    int rear;
    int front;
    int k;
} MyCircularQueue;

MyCircularQueue* myCircularQueueCreate(int k) {
    MyCircularQueue *obj=(MyCircularQueue*)malloc(sizeof(MyCircularQueue));
    //开k+1个空间
    obj->a=(int*)malloc(sizeof(int)*(k+1));
    obj->rear=obj->front=0;
    obj->k=k;
    return obj;
}

bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
    //重合时为空
    return obj->rear==obj->front;
}

bool myCircularQueueIsFull(MyCircularQueue* obj) {
    //rear的下一个是front时为满
    return (obj->rear+1)%(obj->k+1)==obj->front;
}

bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
    //入队列
    //先判满
    if(myCircularQueueIsFull(obj))
        return false;
    
    obj->a[obj->rear]=value;
    obj->rear++;
    //更新rear
    obj->rear %= obj->k+1;

    return true;

}

bool myCircularQueueDeQueue(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return false;
    //出队列
    ++obj->front;
    //更新front
    obj->front %= obj->k+1;
    return true;
}

int myCircularQueueFront(MyCircularQueue* obj) {
   if(myCircularQueueIsEmpty(obj))
        return -1;
    else
         return obj->a[obj->front];
}

int myCircularQueueRear(MyCircularQueue* obj) {
    if(myCircularQueueIsEmpty(obj))
        return -1;
    else
        return obj->a[(obj->rear+obj->k)%(obj->k+1)]; 
}

void myCircularQueueFree(MyCircularQueue* obj) {
    free(obj->a);
    free(obj);
}

结语

本篇介绍了链队列、循环队列的食用方法，由于本人技术不足，如发现有BUG，可以私聊我解决

024EA254

【数据结构】队列(顺序队列、循环队列、链队列）
Jacky_Feng的博客
09-15 5万+
文章目录 前言 一、队列的定义 二、队列的顺序存储结构 1.顺序队列的定义 2.循环队列定义 3.循环队列的基本操作 三、队列的链式存储结构 1.链队列的定义 2.链队列的基本操作 前言 队列也是一种线性表，其特殊性在于队列的基本操作是线性表的子集。队列按“先进先出”的规则进行操作，故称其为操作受限的线性表。 一、队列的定义 队列（queue）是只允许在一端进行插入操作，在另一端进行删除操作的线性表，简称“队”。 队列是一种先进先出（First In First Out）的
队列，顺序队列，循环队列，链式队列
qq_43389859的博客
07-08 938
为了解决“假溢出”现象，使得队列的存储空间得到充分利用，一个巧妙的方法就是将顺序队列的数组看成一个头尾相接的循环结构。队列的头尾相接的顺序存储结构称为循环队列。题：当循环对列为空或满时，都是队尾指针等于队头指针，即rear==front。当rear==front时，该是判满还是判空呢？解决方案：方案一：设置一个计数器，开始时计数器设为0，新元素入队时，计数器加1，元素出队，计数器减1。当计数器==MAXSIZE时，队满；计数器==0时，队空。
队列，顺序队列与循环队列
qq_37020594的博客
09-07 2546
队列   队列是一种特殊的线性表，特殊之处在于它只允许在表的前端(front)进行删除操作，而在表的后端(rear)进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。   队列中的数据元素称为队列元素。队列中没有元素时，称为空队列。队列只允许在一端插入，另一端删除，所以队列是一种先进先出的线性表。 1. 顺序队列   顺序队列存储模式：一维数...
数据结构---循环队列
weixin_49324123的博客
03-03 680
循环队列与普通队列的区别
【数据结构】详解队列和循环队列
m0_52094687的博客
12-23 2735
该博客讲了队列的概念及结构，使用C语言实现队列，又简绍了循环队列，并且通过Leetcode上的一道题，实现循环队列
队列及循环队列
最新发布
2303_79383388的博客
03-23 822
队列及循环队列笔记
JavaScript数据结构之优先队列与循环队列实例详解
01-19
本文实例讲述了JavaScript数据结构之优先队列与循环队列。分享给大家供大家参考，具体如下： 优先队列 实现一个优先队列：设置优先级，然后在正确的位置添加元素。 我们这里实现的是最小优先队列，优先级的值小...
JavaScript队列、优先队列与循环队列
10-21
与普通队列相似，循环队列也需要实现基本的队列操作方法，但由于其循环的特性，其内部的数组操作稍有不同。 优先队列和循环队列都可以用于解决特定问题，优先队列适用于需要根据优先级顺序处理任务的场景，如任务...
java队列实现方法(顺序队列,链式队列,循环队列)
08-28
Java 中提供了多种实现队列的方法，包括顺序队列、链式队列和循环队列等。下面我们将详细介绍每种队列的实现方法和特点。 一、顺序队列 顺序队列是指使用数组来实现队列的数据结构。它的特点是元素在数组中的位置...
队列、循环队列、双端队列详解（含完整代码）
m0_60284144的博客
04-24 3063
队列是一种操作受限的线性表。只允许在表的一端进行插入，在表的另一端进行删除。和日常生活中的队列一样 先入队的元素优先出队，即先进先出。
数据结构之队列
dev晴天的博客
02-07 196
“后进先出”，“先进先出“ 我们经常会听见这两句。然而这两句话代表了两种不同的数据结构，前者我们已经熟悉，接下来我们就探究一下后者。 要点 一、队列（以数组队列为例） 概念: 队列是一种先进先出（FIFO）的数据结构。 特点： 队列内的数据，先入队的取元素时先出去（参考下生活实例图理解）。 与栈的区别（模型） 表面区别 1 相同之处 ：规定好首端尾端后，都是把数据添加到尾端（没有数据时默认...
基本数据结构 java表示（未完）
waj89757的专栏
06-02 1150
1.线性表     顺序表 和 链表 2.栈   链式和数组展现 3.队列（循环队列）  链式和数组展现 4.树 （二叉树）  链式和数组展现 2.栈 见自己的word文档 3.队列 循环队列 　   为充分利用向量空间，克服"假溢出"现象的方法是：将向量空间想象为一个首尾相接的圆环，并称这种向量为循环向量。存储在其中的队列称为循环队列（Circul
数据结构-链队列和循环队列
aaa0329的博客
05-17 1752
一、链队列 需要创建两个指针分别指向队头和队尾，删除元素只能在队头进行，当然添加元素也只能在队尾进行 1.链队列的节点 typedef struct LinkNode{ int data; LinkNode*next; }*LinkNodePtr; 2.链队列 typedef struct LinkQueue{ LinkNodePtr front; LinkNodePtr rear; }*LinkQueuePtr; 3.创建头节点 头指针和尾指针指向头节点 LinkQueueP
第3章 数组队列、循环队列及两者的比较
入凡尘狼性不足
05-26 663
3-5 数组队列
队列——链队列和循环队列
大草的博客
11-03 8930
链队列 转载：https://www.cnblogs.com/muzijie/p/5655228.html 1 链队列的存储结构 　　将对头指针front指向链队列的头结点，队尾指针rear指向终端结点。 空队列时，头指针front和尾指针rear都指向头结点。   链队列的存储结构为： typedef int QElemType; typedef struct QNode...
数据结构之数组队列、循环队列的实现以及它们的区别
08-15 833
每个队列的实现都有注释 仔细看就行 队列接口： package demo; public interface Queue<E> { void enqueue(E e); E dequeue(); E getFront(); int getSize(); boolean IsEmpty(); } 数组队列： package demo; import j...
循环队列与普通队列
WGS.
12-10 907
普通队列 #include "stdio.h" #include "stdlib.h" #include "string.h" #define MAXSIZE 20 //普通队列 typedef struct{ int data[MAXSIZE]; int front; //队头 int rear; //队尾 }Queue; //入队 int enQueue(Queue* q, ...
C++数据结构：普通队列与循环队列
琅嬛福地
06-14 1659
什么是队列？ 队列是一种特殊的线性表，它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作。队列中的数据元素遵循“先进先出”（First In First Out）的原则，简称FIFO结构。 队列分类 普通队列与循环队列，普通队列可以看做是一列数据，环形队列可以看做是一个圆，当普通队列的数据索引可以循环设置时，普通队列就成了循环队列。这两种都可以用数组来实现。 循环队列的C++实现 下面说明用数组实现循环队列的方法 ...
循环队列
热门推荐
smile_zhangw的博客
07-03 5万+
        队列是一种只能在表的一端进行插入运算，在表的另一端进行删除运算的线性表（头删尾插），它的存储方式分为顺序队或链队，以循环队列更常见。       这里仅介绍顺序队以及顺序队存在的假溢出缺陷，进而引出循环队列。顺序队列                在顺序队列中，当队尾指针已经到数组的上界，不能再有入队操作，但其实数组中还有空位置，这就叫做“假溢出”，解决假溢出的途径----采用循环...
评论 5
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

吃椰子不吐壳

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值