leetcode_动态规划_入门总结

四个组成部分

确定状态

• 研究最优策略的最后一步
• 化为子问题

转移方程

• 根据子问题定义直接得到

初始条件和边界情况

• 细心，考虑周全

计算顺序

• 利用之前的计算结果
• 通常一维从小到大，二维从上到下、从左到右

什么问题可以用动态规划解决

1 计数：如有多少种路径 有多少种组合等

2 求最值：如最长上升子序列，最大数字和，最小代价等

3 可行性：如跳跃问题 零钱凑整问题等

下面对这三种题型各列举一个例题进行分析

1.解码方法(计算问题)

leetcode传送门

第一步：确定状态

1.“最后一步”

本题的最后一步有两种情况：

<1>如果最后一个字符在1到9中，那么该字符就可以单独映射一个字母。

<2>如果最后一个字符与它之前的一个字符组合在10到26中，那么这两个字符就可以组合映射一个字母。

2.“子问题”

假设字符串的长度是n
原来我们要寻找的方案是针对整个字符串的
现在我们要寻找的方法是针对前n-1个字符的子字符串
问题的规模减小了，也就是确定了子问题，子问题出来了便确定了状态

第二步：转移方程

设状态num[x]=当前字串的编码方法数
转移方程：num[x]=(condition1)num[x-1]+(condition2)num[x+2]
条件1：if 0<第i个字符映射的数字<10
条件2：if 10<第i和第i-1个字符组合映射的数字<26

第三步：初始条件和边界情况

初始条件：nums[0] = 1
边界情况：不会越界

第四步：计算顺序

由转移方程决定，从小到大
java代码实现：

class Solution {
    public int numDecodings(String s) {
        char[] chars = s.toCharArray();
        int len = s.length();
        int[] nums = new int[len + 1];
        int pre = 0;
        int now = 0;
        int sum = 0;
        nums[0] = 1;
        if (len == 0)
            return 0;
        for (int i = 1; i <= len; i++) {
            now = chars[i-1] - '0';
            if ((now > 0) && (now < 10))
                nums[i] += nums[i - 1];
            if (i > 1) {
                pre = chars[i - 2] - '0';
                sum = pre * 10 + now;
                if ((sum >= 10) && (sum <= 26))
                    nums[i] += nums[i - 2];
            }
        }
        return nums[len];
    }
}

2.炸死敌人（最值问题）

leetcode传送门

题目分析

第一步：确定状态

子问题

第二步：转移方程

第三步：初始条件和边界情况

第四步：计算顺序

java代码：

    //这个题目只能分四个方向分别来做，不能优化为两个或者一个for循环
    //我们只关心空格最多能炸死的敌人的数量，所以假设有敌人和有墙的格子都能够被访问
    public int bompEnemy(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] count = new int[m][n];
        int[][] sum = new int[m][n];
        int max = 0;
        //向上
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                count[i][j] = 0;
                if (grid[i][j] == 2)
                    continue;
                if (grid[i][j] == 1) {
                    count[i][j] = 1;
                }
                if (i > 0)
                    count[i][j] += count[i - 1][j];
                sum[i][j] += count[i][j];
            }
        }
        //向下
        for (int i = m - 1; i >= 0; i--) {
            for (int j = 0; j < n; j++) {
                count[i][j] = 0;
                if (grid[i][j] == 2)
                    continue;
                if (grid[i][j] == 1) {
                    count[i][j] = 1;
                }
                if (i < m - 1)
                    count[i][j] += count[i + 1][j];
                sum[i][j] += count[i][j];
            }
        }
        //向左
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                count[i][j] = 0;
                if (grid[i][j] == 2)
                    continue;
                if (grid[i][j] == 1) {
                    count[i][j] = 1;
                }
                if (j > 0)
                    count[i][j] += count[i][j - 1];
                sum[i][j] += count[i][j];
            }
        }
        //向右
        for (int i = 0; i < m; i++) {
            for (int j = n - 1; j >= 0; j--) {
                count[i][j] = 0;
                if (grid[i][j] == 2)
                    continue;
                if (grid[i][j] == 1) {
                    count[i][j] = 1;
                }
                if (j < n - 1)
                    count[i][j] += count[i][j + 1];
                sum[i][j] += count[i][j];
            }
        }
        for (int i = 0; i < m; i++) {
            for(int j=0;j<n;j++)
                if(grid[i][j]==0)
                    max = Integer.max(max, sum[i][j]);
        }
        return max;
    }

3.粉刷房子（最值问题）

leetcode传送门

第一步：确定状态

1.“最后一步”

当最后一栋房子颜色为红色时：

当最后一栋房子颜色为蓝色时：

当最后一栋房子颜色为绿色时：

2.子问题

第二步：转移方程

第三步：初始条件和边界情况

第四步：计算顺序

Java代码：

//用数组a来存储三种颜色的最小成本
    public int paintHouse(int[][] cost) {
        int m = cost.length;
        int[][] a = new int[m + 1][3];
        a[0][0] = a[0][1] = a[0][2] = 0;
        int min = Integer.MAX_VALUE;
        for (int i = 1; i <= m; i++) {
            a[i][0] = Integer.min(a[i - 1][1], a[i - 1][2]) + cost[i - 1][0];
            a[i][1] = Integer.min(a[i - 1][0], a[i - 1][2]) + cost[i - 1][1];
            a[i][2] = Integer.min(a[i - 1][0], a[i - 1][1]) + cost[i - 1][2];
        }
        min = Integer.min(Integer.min(min, a[m][0]), Integer.min(a[m][1], a[m][2]));
        return min;
    }

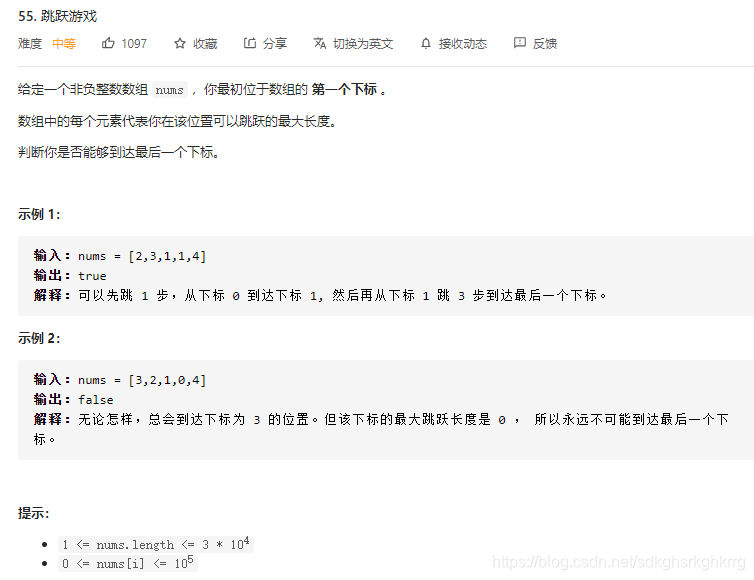
4.跳跃游戏（可行性问题）

leetcode传送门

第一步：确定状态

1. “最后一步”

2.子问题

第二步：转移方程

第三步：初始条件和边界情况

初始条件即f[0]=true，因为青蛙初始状态是蹲在第一块石头上的，所以第一块石头是肯定可以到达的。
边界情况无

第四步：计算顺序

Java代码：

    public boolean canJump(int[] nums) {
        int len = nums.length;
        boolean[] jump = new boolean[len];
        jump[0] = true;
        for (int i = 1; i < len; i++) {
            for (int j = 0; j < i; j++) {
                if ((jump[j]) && (j + nums[j] >= i)) {
                    jump[i] = true;
                    break;
                }
            }
        }
        return jump[len - 1];
    }