7-线性分类-逻辑回归-logistics regression

1. 从线性回归到线性分类

我们之前用到的线性回归就是将数据$(x_i,y_i)$用$W^{T}X$进行拟合，而现在的线性分类是一个{0,1}或者(0,1)分类问题，线性回归到线性分类是通过激活函数来实现数据的映射的。通过映射(激活函数)完成数据的转换 W T X ⟼ { 0 , 1 } W^TX \longmapsto\{0,1\} WTX⟼{0,1}
在逻辑回归(logistics regression)中常用的激活函数为：
$$\sigma (z)=\frac{1}{1+e^{-z}}\text{\hspace{1em}(1)}$$
注：激活函数有如下性质：
$1.li{m}_{z\to +\infty }\sigma (z)=1$
$2.li{m}_{z\to 0}\sigma (z)=\frac{1}{2}$
$3.li{m}_{z\to -\infty }\sigma (z)=0$
这个激活函数叫sigmoid函数：图像如下：

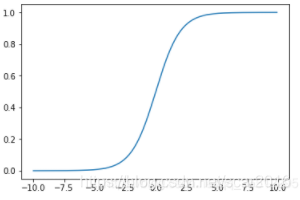
通过激活函数(sigmoid函数)我们可以实现数据$\mathbb{R}⟼(0,1)$,我们将$W^{T}X带入sigmoid函数可得：$
$$p1=p(y=1|x)=\sigma (w^{T}x)=\frac{1}{1+e^{-w^{T}x}}=\psi (w,x);y=1\text{\hspace{1em}(2)}$$
$$p2=p(y=0|x)=1-\sigma (w^{T}x)=\frac{e^{-w^{T}x}}{1+e^{-w^{T}x}}=1-\psi (w,x);y=0\text{\hspace{1em}(3)}$$
我们可以由上式(2),(3)合并后得到如下公式：
$$p(y|x)=p_1^y\cdot p_2^{1-y}\text{\hspace{1em}(4)}$$
我们知道了p(y|x)单个的概率密度后，我们可以极大似然估计法求出对应的值：

2.最大后验估计MLE

$MLE=\hat{w}=argma{x}_w{\prod }_{i=1}^n\log p(y_i|x_i)={\prod }_{i=1}^n\log p_1^y\cdot p_2^{1-y}$

$=argma{x}_w{\sum }_{i=1}^n[y\log p_1+(1-y)\log p_2]$

$\frac{1}{1+e^{-w^{T}x}}=\psi (w,x);y=1$

$\frac{e^{-w^{T}x}}{1+e^{-w^{T}x}}=1-\psi (w,x);y=0$;代入可得如下：

$$MLE=argma{x}_w\sum _{i=1}^n[y\log \psi (x,w)+(1-y)\log (1-\psi (x,w)]\text{\hspace{1em}(5)}$$

由上式可以看出：$y\log \psi (x,w)+(1-y)\log (1-\psi (x,w))就是一个交叉熵的表达形式(Cross\_Entropy)$以上我们成功的找到了目标函数的形式，可以描述为:

$$ML{E}_{(max)}=Loss\_Functio{n}_{min}cross\_entropy)\text{\hspace{1em}(6)}$$

综上所述，逻辑回归的优化问题可以转换成一个Cross Entropy的优化问题。