数组问题一_数组怎么知道有没有被选中-优快云博客

本文深入探讨了数组中的算法问题，包括找出出现次数大于数组长度一半的数、超过数组长度N/K的数，以及数组的奇偶位置调整。此外，还介绍了如何在O(N)时间和O(K)空间复杂度内找到数组中出现次数大于N/K的数，以及如何保证数组中偶数在偶数位置、奇数在奇数位置。文章进一步讨论了快速排序和BFPRT算法在寻找数组中第k大数的应用。

一找出数组中出现次数大于数组长度一半和 N/K 的数

1、找出数组中出现次数大于数组长度一半的数

一个数组中出现次数大于数组长度一般的数显然最多只有一个。

题目：在数组中找到出现次数大于数组长度一半的数。要求：时间复杂的 O(N)，额外空间复杂度 O(1)。

HashMap方法

public int majorityElement(int[] nums) {
       Map<Integer, Integer> map = new HashMap<>();
         for (int i = 0; i < nums.length; i++) {
             int val=1;
             if(map.containsKey(nums[i])){
                 val=map.get(nums[i]);
                 val++;
             }
             map.put(nums[i], val);
         }
         for (int i : map.keySet()) {
             if (map.get(i) > nums.length / 2) {
                 return i;
             }
         }
        return 0;
   }

抵消法基本思想：举个例子，敌我两国交战，我国的士兵人数超过敌国士兵人数，且士兵交战同归于尽，最后一定是我国获胜。拓展到多国交战，同理，我国士兵人数超过其他多国士兵总和，且士兵交战同归于尽，最后一定是我国获胜。

回到题目上来，数组的里面所包含的数就是交战国家的士兵，里面出现次数超过一半的数字就是我国的士兵，其他的数字就是别国的士兵，比如{1, 2, 3, 2, 2, 2, 5, 4, 2] 则2是我国士兵，1是甲国士兵，3是乙国士兵，以此类推。因为数字2是超过数组长度一半的，故无论士兵是以哪种方式（可能2与1，可能1与3，可能2与3等等）同归于尽的，最后剩下的一定是2。因此，采取这种思想，设置一个投票变量count 代表目前还活着的士兵数量，从头遍历数组。

public class FindMajority {
 
    // 找到出现次数超过数组一半的数：如果有，也只有一个
    public static int findOverHalfNum(int[] arr){
        if(arr == null || arr.length < 1){
            return Integer.MIN_VALUE;
        }
        int candiate = 0;
        int count = 0;
 
        for(int i = 0; i < arr.length; i++){
            if(count== 0){
                // 还没有候选人，当前值直接设置为候选人
                candiate = arr[i];
                count++;
            }else if(arr[i] == candiate){
                // 有候选人，并且当前数和候选人一致
                count++;
            }else{
                // 有候选人，但是当前数和候选人不一致
                count--;
            }
        }
 
        // 最后剩下的候选人是可能出现次数超过数组总长度一半的数，但是还需要校验下
        if(count != 0){
            count = 0;
            for(int i = 0; i < arr.length; i++){
                if(arr[i] == candiate){
                    count++;
                }
            }
            if(count > arr.length / 2){
                return candiate;
            }
        }
        return Integer.MIN_VALUE;
    }
}

2、找出数组中出现次数大于数组长度 N/K 的数。要求：时间复杂度为 O(NK)，额外空间复杂度为 O(K)。

分析：

1、一次删除 K 个不同的数，那么你 N 个数，最多能减 N/K次，所以大于 N / K 的数一定会剩下来；

2、给你 K ，最多有 K - 1 个数是大于 N / K 【比如 > N / 4 的最多只有 3 个】，所以保留 K - 1 个候选人即可；

步骤：

1、候选表 HashMap：key为（K - 1）个候选 candiate，value 为它们分别出现的次数;

2、遍历到 arr[i] 时，看 arr[i] 是否在候选人中，如果与某一个候选人相同，就把属于那个候选的点数统计加 1，如果与所有的候选都不相同，先看当前的候选是否选满了，候选表中的大小为 K - 1 个，就是满了；否则就是没有选满。

如果不满，则把 arr[i] 作为一个新的候选，属于它的点数初始化为 1；
如果已满，说明此时发现了 k 个不同的数，arr[i] 就是第 k 个。此时把每一个候选各自的点数全部减 1，表示每个候选“付出”一个自己的点数，当前数也不要。如果某些候选的点数在减 1 之后等于 0，则还需要把这些候选人从候选表中删除，候选又变为不满的状态。

在上述过程结束后，还需要再遍历一次，验证被选出来的所有候选有哪些出现次数真的大于 N / K。

public class FindMajority {
 
    /**
     * 找到数组中出现次数大于 N/K 的数：最多有 K - 1 个
     */
    public static ArrayList<Integer> findOverKTimes(int[] arr, int k){
        if(arr == null || arr.length < k){
            return null;
        }
 
        // 候选表：用HashMap记录最多K-1个出现次数大于N/K的数的情况
        HashMap<Integer, Integer> candiates = new HashMap<>();
        for(int i = 0; i < arr.length; i++){
            // 当前数在候选表中,出现次数加1
            if(candiates.containsKey(arr[i])){
                candiates.put(arr[i], candiates.get(arr[i]) + 1);
            }else if(candiates.size() < k - 1){
                // 当前数不在候选表中，并且候选表还没有满时，直接插入
                candiates.put(arr[i], 1);
            }else{
                // 当前数不在候选表中，并且候选表已经满了，则将所有候选者次数都减1，当前数也不要（因为当前数次数也为1）
                allCandiatesDeleteOne(candiates);
            }
        }
 
        ArrayList<Integer> list = new ArrayList<>();
        // 还有候选人
        if(!candiates.isEmpty()){
            // 得到候选人的真实个数
            HashMap<Integer, Integer> reals = getReals(arr, candiates);
            for(Map.Entry<Integer, Integer> set : reals.entrySet()){
                if(set.getValue() > arr.length / k){
                    list.add(set.getKey());
                }
            }
        }
        return list;
    }
 
    public static void allCandiatesDeleteOne(HashMap<Integer, Integer> candiates){
        for(Map.Entry<Integer, Integer> candiate : candiates.entrySet()){
            Integer count = candiate.getValue();
            if(count == 1){
                // 当前候选人出现的次数仅为1，则直接从候选表中删除
                candiates.remove(candiate.getKey());
            }else{
                // 出现次数减1
                candiates.put(candiate.getKey(), --count);
            }
        }
    }
 
    public static HashMap<Integer, Integer> getReals(int[] arr, HashMap<Integer, Integer> candiates){
        HashMap<Integer, Integer> res = new HashMap<>();
        for(Map.Entry<Integer, Integer> set : candiates.entrySet()){
            int candiate = set.getKey();
            int count = 0;
            for(int i = 0; i < arr.length; i++){
                if(arr[i] == candiate){
                    count++;
                }
            }
            res.put(candiate, count);
        }
        return res;
    }
}

二数组的奇偶位置问题

1题目：给定一个整型数组，请在原地调整这个数组，保证要么偶数位置上都是偶数，或者奇数位置上都是奇数。

要求：时间复杂度 O(N)，额外空间复杂度 O(1)。

这个题目需要注意的是：偶数在偶数的位置、奇数在奇数的位置，这两个条件满足其一就行了。

下面的代码中，将最后一个元素作为发货点，根据自己值的奇偶性和当前数组 odd 和 even 指针指向的元素进行交换，这样不停的交换。最后如果有一个指针越界了，那对应的规则就排在了对应的位置上了。

这个题目的代码量不是很大，也没有特殊的算法，但是编程技巧确实很好。

public class EvenInEvenOddInOdd {
 
    public static void getOrder(int[] arr){
        if(arr == null || arr.length < 2){
            return;
        }
        int even = 0;  // 指向偶数的位置
        int odd = 1;   // 指向奇数的位置
        // 发货点：每次把最后一个数根据它是奇数还是偶数和前面对应奇偶指针上的数互换位置
        int end = arr.length - 1;
        while(odd < arr.length && even < arr.length){
            if(arr[end] % 2 == 0){
                // 往even指针上发货,然后even指针后移两位
                swap(arr, end, even);
                even += 2;
            }else{
                // 往odd指针上发货,然后odd指针后移两位
                swap(arr, end, odd);
                odd += 2;
            }
        }
    }
 
    public static void swap(int[] arr, int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
}

2.题目：输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有奇数位于数组的前半部分，所有偶数位于数组的后半部分。

这个题目要求把奇数放在数组的前半部分，偶数放在数组的后半部分，因此所有的奇数应该位于偶数的前面，也就是说我们在扫描这个数组的时候，如果发现有偶数在奇数的前面，我们可以交换他们的数序，交换之后就符合要求了。

因此我们可以维护两个指针，第一个指针初始化时指向数组的第一个数字，它只向后移动；第二个指针初始化时指向数组的最后一个数字，它指向前移动。在两个指针相遇之前，第一个指针总是位于第二个指针的前面。如果第一个指针的数字是偶数，并且第二个指针指向的数字是奇数，我们就交换两个数字。

下面看一个案例：

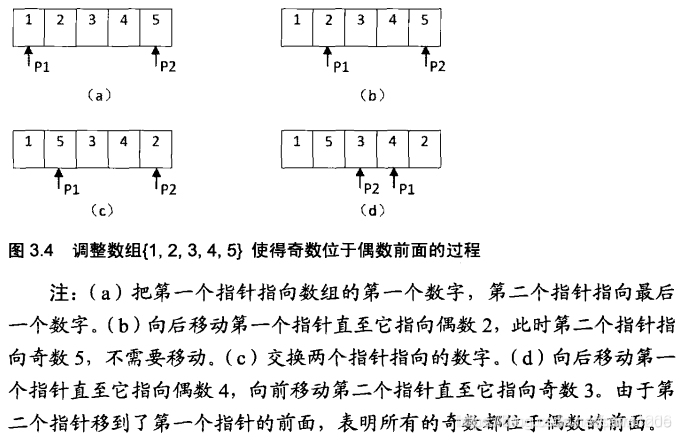
基于这个分析，我们可以写出如下代码：

public class OddBeforeEven {
 
	public int[] recorderOddEven(int[] data, int length){
		if(data == null && length <= 0){
			return null;
		}
		
		int begin = 0;
		int end = length - 1;
		
		// begin指针要位于end指针前面
		while(begin < end){
			// 向后移动begin指针，直到它指向偶数
			if(begin < end && (data[begin] & 0x1) != 0){
				begin++;
			}
			
			// 向前移动end指针，直到它指向奇数
			if(begin < end && (data[end] & 0x1) == 0){
				end--;
			}
			
			// 交换奇数和偶数的位置
			if(begin < end){
				int temp = data[begin];
				data[begin] = data[end];
				data[end] = temp;
			}
		}
		return data;
	}
	
	// 测试
	public static void main(String[] args) {
		OddBeforeEven obe = new OddBeforeEven();
		int[] arr= {1,2,3,4,5,6,12,7,8,9,10};
		int[] data = obe.recorderOddEven(arr, arr.length);
		System.out.println(Arrays.toString(data));
	}
}

考虑可扩展的解法，能秒杀 Offer

如果是面试应届毕业生或者工作时间不长的程序员，面试官会满意前面的代码，但如果应聘者申请的是资深的开发职位，那面试官可能会接着问几个问题。

面试官：如果把题目改成数组中的数按照大小分为两部分，所有的负数在所有的非负数的前面，该怎么做？

如果再把题目改改，变成把数组中的数分成两部分，能被3整除的数都在不能被3整除的数的前面，怎么办？

这就是面试官在考察我们对可扩展性的理解，即希望我们能够给出一个模式，在这个模式下能够很方面第把已有的解决方案扩展到同类型的问题上去。

于是我们写出下面可扩展性的代码：

public class OddBeforeEvenExtension {
 
	public int[] recorderOddEven(int[] data, int length){
		if(data == null && length <= 0){
			return null;
		}
		
		int begin = 0;
		int end = length - 1;
		
		// begin指针要位于end指针前面
		while(begin < end){
			// 向后移动begin指针，直到它指向偶数
			if(begin < end && !isEven(data[begin])){
				begin++;
			}
			
			// 向前移动end指针，直到它指向奇数
			if(begin < end && isEven(data[end])){
				end--;
			}
			
			// 交换奇数和偶数的位置
			if(begin < end){
				int temp = data[begin];
				data[begin] = data[end];
				data[end] = temp;
			}
		}
		return data;
	}
    // 扩展函数
	private boolean isEven(int data) {
		return (data & 0x1) == 0;
	}
 
	// 测试
	public static void main(String[] args) {
		OddBeforeEvenExtension obe = new OddBeforeEvenExtension();
		int[] arr= {1,2,3,4,5,6,12,7,8,9,10};
		int[] data = obe.recorderOddEven(arr, arr.length);
		System.out.println(Arrays.toString(data));
	}
}

这样如果增加额外的判断条件，只需要改变isEven函数中的逻辑即可，对于recorderOddEven函数中的主体逻辑框架无需改变，这样就实现了解耦。

3.题目：输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

1、要想保证原有的次序，则只能顺序移动或者相邻交换；

2、i 从左到右开始遍历，找到第一个偶数；

3、j 从 i+1 开始向后找，直到找到第一个奇数；

4、将 [ i , ... . j - 1 ] 的元素整体后移一位，最后将找到的奇数放入 i 位置，然后 i++；

5、终止条件，j 向后遍历查找失败，即后面没有奇数了。

/**
 * 输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，
 * 所有的偶数位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。
 */
public class OddBeforeEven_Improved {
 
	public int[] reOrderArray(int[] arr) {
        if(arr == null && arr.length <= 0){
        	return null;
        }
        
        int i = 0, j;   
        while(i < arr.length){
        	while(i < arr.length && !isEven(arr[i])){
        		i++;
        	}
        	// i指向偶数时，j从i+1开始向后遍历找奇数
        	j = i + 1;  
        	while(j < arr.length && isEven(arr[j])){
        		j++;
        	}
        	if(j < arr.length){
        		// 将[i,...,j-1]的元素整体后移1位，最后将找到的奇数放入i位置
        		int temp = arr[j];
        		for(int k = j - 1; k >= i; k--){
        			arr[k + 1] = arr[k];
        		}
        		arr[i++] = temp;
        	}else{
        		// 查找失败
        		break;
        	}
        }
        return arr;
    }
 
	// 判断n是否是偶数
	private boolean isEven(int n) {
		if(n % 2 == 0){
			return true;
		}
		return false;
	}
	
	// 测试
	public static void main(String[] args) {
		OddBeforeEven_Improved obe = new OddBeforeEven_Improved();
		int[] arr= {1,2,3,4,5,6,12,7,8,9,10};
		int[] data = obe.reOrderArray(arr);
		System.out.println(Arrays.toString(data));
	}
}

上面这种解法每次发现一个奇数在偶数后面，就需要搬移他们之间所有的元素，时间复杂度为O(n^2)。下面我们将使用一种空间换时间的思想，将时间复杂度降低为O(n)。

具体做法如下:首先统计奇数的个数，然后新建一个与原数组等长的数组，设置两个指针，奇数指针从0开始，偶数指针从奇数个数的末尾开始遍历填数。

public class OddBeforeEven_Improving {
 
	public int[] reOrderArray(int[] arr){
		if(arr.length == 0 || arr.length == 1){
			return arr;
		}
		
		int oddCount = 0, oddBegin = 0;
		int[] newArr = new int[arr.length];
		// 统计原数组中奇数的个数
		for (int i = 0; i < arr.length; i++) {
			if((arr[i] & 1) == 1){
				oddCount++;
			}
		}
		
		for (int i = 0; i < arr.length; i++) {
			if((arr[i] & 1) == 1){
				// 在新数组中，先放奇数，从头开始放
				newArr[oddBegin++] = arr[i];
			}else{
				// 偶数从奇数总个数后开始放
				newArr[oddCount++] = arr[i];
			}
		}
		
		for (int i = 0; i < arr.length; i++) {
			arr[i] = newArr[i];
		}
		return arr;
	}
	
 
	// 测试
	public static void main(String[] args) {
		OddBeforeEven_Improving obe = new OddBeforeEven_Improving();
		int[] arr= {1,2,3,4,5,6,12,7,8,9,10};
		int[] data = obe.reOrderArray(arr);
		System.out.println(Arrays.toString(data));
	}
}

三数组的度（字节跳动面试题）

题目：给定一个非空且只包含非负数的整数数组 nums, 数组的度的定义是指数组里任一元素出现频数的最大值。你的任务是找到与 nums 拥有相同大小的度的最短连续子数组，返回其长度。

示例 1:

输入: [1, 2, 2, 3, 1]

输出: 2

解释:

输入数组的度是2，因为元素1和2的出现频数最大，均为2.

连续子数组里面拥有相同度的有如下所示:

[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]

最短连续子数组[2, 2]的长度为2，所以返回2.

示例 2:

输入: [1,2,2,3,1,4,2]

输出: 6

注意:

nums.length 在1到50,000区间范围内。

nums[i] 是一个在0到49,999范围内的整数。

思路

首先需要找到数组中出现次数最多的数，并且还需要知道它们在数组中第一次和最后一次出现的位置。需要注意的是出现次数最多的数可能并不唯一，那就需要比较它们在原数组中代表的子数组哪个小就取哪个。

下面用桶实现，O(N) 的时间复杂度：

public class FindShortestSubArray_697 {
 
    public int findShortestSubArray(int[] nums) {
 
        if(nums == null || nums.length < 1){
            return 0;
        }
 
        // 找到数组中最大元素的值
        int maxVal = -1;
        for(int i = 0; i < nums.length; i++){
            if(nums[i] > maxVal){
                maxVal = nums[i];
            }
        }
 
        // 创建 max + 1 个桶
        int[] counts = new int[maxVal + 1];      // 存储数组元素出现的次数
        int[] beginIndex = new int[maxVal + 1];  // 存储元素的起始下标
        int[] endIndex = new int[maxVal + 1];    // 存储元素的结束下标
 
        for(int i = 0; i < nums.length; i++){
            if(counts[nums[i]] == 0){
                beginIndex[nums[i]] = i;
            }
            counts[nums[i]]++;
            // 结束位置都是遇到就更新，这样就可以记录到最后一次出现的位置
            endIndex[nums[i]] = i;
        }
 
        // 查找元素出现次数最多(count[i]最大)，且长度最短（endIndex[i] - beginIndex[i]最小）的长度
        int minSubLength = Integer.MAX_VALUE;
        int maxCount = 0;
        for(int i = 0; i < counts.length; i++){
            int subLen = endIndex[i] - beginIndex[i];
            if(counts[i] > maxCount){
                maxCount = counts[i];
                minSubLength = subLen;
            }else if(counts[i] == maxCount && subLen < minSubLength){
                // 要考虑出现次数相等，但是子数组长度不同的情况
                minSubLength = subLen;
            }
        }
    return minSubLength + 1;
    }
}

四 BFPRT 算法、快排解决第 k 大数问题

问题：求一个数组中的第 k 小 / 大的数。

说明：这道题求解不难，主要的目的是为了引出快排算法的应用（partiotion）和 BFPRT 算法

方法1：暴力解法

其实我们很容易想到先将这个数组排好序，再直接取出数组中下标为 k - 1 的数即可。

public class FindKthNumByQuickSort {
 
    // 暴力解法
    public static int getKthNum(int[] arr, int k){
        if(arr == null || arr.length < 1 || k < 0){
            return Integer.MIN_VALUE;
        }
 
        Arrays.sort(arr);
        return arr[k - 1];
    }
}

方法2：快排实现【笔试版+面试版】

//快速排序算法
 static void quicksort(int arrs[], int low, int high) {
        int dp;
        if (low<high) {
            dp = partition(arrs, low, high);
            quicksort(arrs, low, dp - 1);
            quicksort(arrs, dp + 1, high);
        }
    }
  public static int partition(int[] arrs, int low, int high){
        // 固定的切分方式
        int key = arr[low];
        while(low < high){
            // 从后半部分往前半部分扫描
            while(low<high && arr[high] <= key){
                high--;
            }
            // 交换位置，把后半部分比基准点位置元素值小的元素交换到前半部分的low位置处
            arr[low] = arr[high];
 
            // 从前半部分往后半部分扫描
            while(low<high && arr[low] > key){
                low++;
            }
            arr[high] = arr[low];
        }
        arr[high] = key;
        return high;
    }

快速排序将比关键字大的元素从前面移动到后面，比关键字小的元素从后面直接移动到前面，从而减少了总的比较次数和移动次数，同时采用”分而治之“的思想，把大的拆分为小的，小的再拆分为更小的，其原理如下：通过一趟排序将待排序的数组分成两个部分，其中一部分记录的是比关键字更小的，另一部分是比关键字更大的，然后再分别对着两部分继续进行排序，直到整个序列有序；

步骤：代码也很容易理解，其实就是一个“填坑”的过程

1、第一个“坑”挖在每次排序的第一个位置 arr[low]，从序列后面往前找第一个比 pivot 小的数来把这个“坑”填上，这时候的“坑”就变成了当前的 arr[high]；

2、然后再从序列前面往后用第一个比 pivot 大的数把刚才的“坑”填上；

3、如此往复，始终有一个“坑”需要我们填上，直到最后一个“坑”出现，这个“坑”使用一开始的 pivot 填上就可以了，而这个“坑”的位置也就是 pivot 该填上的正确位置，我们再把这个位置返回，就可以把当前序列分成两个部分。再依次这样操作最终就达到排序的目的了【为什么 low 和 high 相遇处就是 pivot 的位置？因为 high 右边一定是 >= pivot的，low 左边一定是

说明：快排的 partition 函数有很多的应用，主要它可以将一个数组基于 key 划分成大于它的和小于它的两部分，利用这个 key 的下标可以做很多事情。

有一个快速排序比较详细的解释参考https://blog.youkuaiyun.com/shujuelin/article/details/82423852

public class FindKthNumByQuickSort {
 
    public static void quickSort(int[] arrs,int low,int high,int k) {
		int index = partition(arrs,low,high);
		if(k-1==index) 
			System.out.println("第"+k+"大元素为"+arrs[index]);
		else if(k-1<index)
			quickSort(arrs,low,index-1,k);
		else
			quickSort(arrs,index+1,high,k);
	}
	
	public static int partition(int[] arrs,int low,int high) {
		int key = arrs[low];
		while(low<high) {
			while(low<high&&arrs[high]<=key) {
				high--;
			}
			arrs[low] = arrs[high];
			while(low<high&&arrs[low]>key) {
				low++;
			}
			arrs[high] = arrs[low];
		}
		arrs[high] = key;
		return high;
	}
 }

方法3：BFPRT 算法实现【面试优化版】

与快排实现的区别在于它不是随机选择用于划分的那个数，而是选择中位数组的中位数，这样选出的数能保证左右两边都至少有 3N/10 的数据，而不像随机选择那样左右两边数据量不确定。

算法流程：

1、得到中位数组中的中位数

相邻 5 个数为一组（0-4，5-9.....），最后一个组剩几个就有几个[因为是逻辑上的划分，所以不花时间]；
每一个小组内排序【5 个数排序是O（1），共有约 N/5 个小组，所以时间复杂度是 O(N/5)】；
把每个小组中的中位数拿出来组成一个新数组：中位数数组【因为长度为 N/5, 所以是 O(N)】；
递归调用 bfprt ，求出中位数数组的中位数【bfprt 解决的是第 k 大的问题，即排好序后位于 k-1 的数】[时间复杂度 T(N/5)]。

2、快排划分区间

可以采用荷兰国旗问题的解决方案将原数组划分成三堆，看 = 部分位置有没有命中 k，如果没有，且位置 < k ，那么排右边，否则排左边，知道命中就返回【因为选出的数能保证左右两边都至少有 3N/10 的数据，即下一次最多只有 7N/10 的数据，因为是递归，所以时间复杂度是 T(7N/10)】。

3、时间复杂度

BFPRT 时间复杂度为：T(N) = T(N/5) + T(7N/10) + O(N) +O（N/5) => O（N）

为什么选出的数能保证左右两边都至少有 3N/10 的数据？

我们先把数每五个分为一组。同一列为一组。排序之后，第三行就是各组的中位数。我们把第三行的数构成一个数列，递归找，找到中位数。这个黑色框为什么找的很好。因为他一定比A3、B3大，而A3、B3、C3又在自己的组内比两个数要大。我们看最差情况：就算其它的数都比 C3 大，也至少有 3/10 的数据比它小。

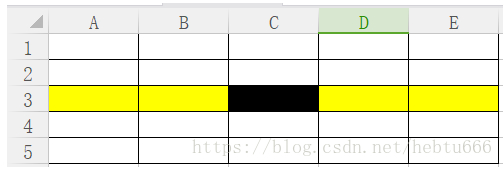
代码实现

public class BFRPT {
 
    public static int getMinKth(int[] arr, int k){
        if(arr == null || arr.length == 0 || k < 0 || k >= arr.length){
            return Integer.MIN_VALUE;
        }
 
        //返回从小到大，位于 k-1 位置的数字，就是第 k 大的数
        int res = bfrpt(arr, 0, arr.length - 1, k - 1);
        System.out.println(res);
        return res;
    }
 
    // 在 left,right 范围上，找到从小到大排序为 p 的数，即为第 p+1 小的数
    public static int bfrpt(int[] arr, int left, int right, int p){
        if(left == right){
            return arr[left];
        }
 
        // bfrpt算法：选择中位数数组中的中位数来作为基准划分原数组，可以每次确定甩掉 3N/10 的数据量
        int num = medianOfMedians(arr, left, right);
        int[] index = partition(arr, left, right, num);
        if(p >= index[0] && p <= index[1]){
            return arr[p];
        }else if(p < index[0]){
            return bfrpt(arr, left, index[0] - 1, p);
        }else{
            return bfrpt(arr, index[1] + 1, right, p);
        }
    }
 
    // 根据数num作为基准对数组arr上left到right的范围进行划分（快排/荷兰国旗）
    public static int[] partition(int[] arr, int left, int right, int num){
        int less = left - 1;
        int more = right + 1;
        int cur = left;
        while(cur < more){
            if(arr[cur] < num){
                swap(arr, ++less, cur++);
            }else if(arr[cur] > num){
                swap(arr, --more, cur);
            }else{
                cur++;
            }
        }
        return new int[]{less + 1, more - 1};
    }
 
    // 求中位数数组中的中位数
    public static int medianOfMedians(int[] arr, int left, int right){
        int num = right - left + 1;
        int offset = num % 5 == 0 ? 0 : 1;
        int[] mArr = new int[num / 5 + offset];  // 中位数数组
        int index = 0;
        for(int i = left; i < right; i = i + 5){
            // 从1开始，而不是从0开始
            mArr[index++] = getMedian(arr, i, Math.min(right, i + 4));
        }
        return bfrpt(mArr, 0, mArr.length - 1, mArr.length / 2);
    }
 
    public static int getMedian(int[] arr, int left, int right){
        insertSort(arr, left, right);
        return arr[(left + right) / 2];
    }
 
    // 因为只对5个数排序，所以选择插入排序
    public static void insertSort(int[] arr, int left, int right){
        for(int i = left + 1; i <= right; i++){
            // 在前面的有序数组中找到自己的位置
            for(int j = i; j > left; j--){
                if(arr[j - 1] > arr[j]){
                    swap(arr, j - 1, j);
                }else{
                    break;
                }
            }
        }
    }
 
    public static void swap(int[] arr, int i, int j){
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
 
    public static void main(String[] args) {
        int[] arr = {6, 9, 1, 3, 1, 2, 2, 5, 6, 1, 3, 5, 9, 7, 2, 5, 6, 1, 9};
        getMinKth(arr, 5);
    }
}