深度学习数据扩充

俺最近在做深度学习的数据扩充，心得愿与小伙伴们分享

注意喽：有四个程序，我都公布啦

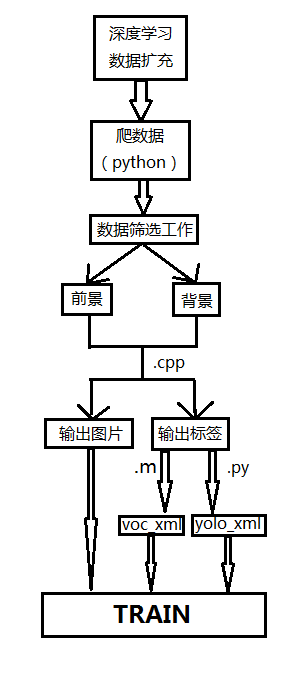
c++源程序如下（感觉代码效率不高，小伙伴们有任何意见希望不吝赐教）：

 

#include <iostream>
#include <cv.h>
#include <highgui.h>
#include <fstream>
#include <string>
#include <vector>
#include <io.h>
#include "stdlib.h"
#include <cstdlib>
#include <typeinfo> 

using namespace std;
using namespace cv;

void getFiles(string path, vector<string>& files)
{
	long hFile = 0;
	struct _finddata_t fileinfo;
	string p;
	if ((hFile = _findfirst(p.assign(path).append("\\*.jpg").c_str(), &fileinfo)) != -1)
	{
		do
		{
			files.push_back(p.assign(path).append("\\").append(fileinfo.name));

		} while (_findnext(hFile, &fileinfo) == 0);
		_findclose(hFile);
	}
}

char * hand_path = "F:\\opencv_extract\\test\\original_images";
char * background_path = "F:\\opencv_extract\\test\\background";

int main()
{	
	vector<string> hand_file;
	vector<string> background_file;

	getFiles(hand_path, hand_file);
	getFiles(background_path, background_file);

	int size_hand_file = hand_file.size();
	int size_background_file = background_file.size();

	for (int i = 0; i < size_hand_file; i++)
	{
		for (int j = 0; j < size_background_file; j++)
		{
			Mat hand_img = imread(hand_file[i]);
			Mat size_hand;
			Size size;
			size.height = 200;
			size.width = hand_img.cols * 200 / hand_img.rows;
			resize(hand_img, size_hand, size);

			Mat background = imread(background_file[j]);
			Mat size_background;
			CvSize back_size;
			back_size.height = 500;
			back_size.width = background.cols * 500 / background.rows;
			resize(background, size_background, back_size);

			////复制图片至另外一张图片////

			for (int row = 0; row < size_hand.rows; row++)
			{
				for (int col = 0; col < size_hand.cols; col++)
				{
					int move_row = row + 150;
					int move_col = col + 150;
					size_background.at<Vec3b>(move_row, move_col)[0] = size_hand.at<Vec3b>(row, col)[0];
					size_background.at<Vec3b>(move_row, move_col)[1] = size_hand.at<Vec3b>(row, col)[1];
					size_background.at<Vec3b>(move_row, move_col)[2] = size_hand.at<Vec3b>(row, col)[2];
				}
			}

			char save_img[40];
			int handfile_size = hand_file[i].size();
			char handfile_name[10];
			for (int x = 0; x < 10; x++)
			{
				int y = x + handfile_size - 9;   //hand1.jpg的长度,根据需要进行修改
				handfile_name[x] = hand_file[i][y];
			}

			IplImage *src;
			src = &IplImage(size_background);
			sprintf(save_img, "F:\\opencv_extract\\test\\img\\%s", handfile_name);
			cvSaveImage(save_img, src);

			////存储xml////

			int min_x = 150;
			int min_y = 150;
			int max_x = 150 + size_hand.cols;
			int max_y = 150 + size_hand.rows;
			int array[] = { min_x, min_y, max_x, max_y };
			
			char save_xml[40];
			char xml_name[6];
			for (int a = 0; a < 6; a++)
			{
				int b = a + handfile_size - 9; 
				xml_name[a] = hand_file[i][b];
				if (b == handfile_size - 4)  //hand1.jpg前hand1的长度，根据需要进行修改
				{
					xml_name[a] = '\0';
					break;
				}
			}
			sprintf(save_xml, "F:\\opencv_extract\\test\\xml\\%s.txt", xml_name);

			ofstream outfile;
			outfile.open(save_xml, 'w');
			outfile << handfile_name << " " << 1 << " " << "[" << endl;
			for (int k = 0; k < 4; k++)
			{
				if (k < 3)
				{
					outfile << array[k] << "," << ' ' << endl;
				}
				else
				{
					outfile << array[k] << "]" << endl;
				}
			}
			outfile.close();
		}
	}
	return 0;
}

 

附件：

1、爬数据python工具：链接：http://pan.baidu.com/s/1pLCTzwn 密码：tkpz

2、cpp工程：链接：http://pan.baidu.com/s/1hsAzN7I 密码：5gof

3、voc标签格式程序：链接：http://pan.baidu.com/s/1c19BQbI 密码：v1al

4、yolo标签格式程序：链接：http://pan.baidu.com/s/1nvnpcNn 密码：lpk5

 

效果图如下：

 +    = 

 

 

任何问题请加唯一QQ2258205918（名称samylee）！

或唯一VX：samylee_csdn