时间复杂度

最新推荐文章于 2025-03-10 20:16:12 发布

临海听风V

最新推荐文章于 2025-03-10 20:16:12 发布

阅读量186

点赞数

分类专栏：笔试面试算法、数据结构

本文链接：https://blog.youkuaiyun.com/samuelandkevin/article/details/104757368

版权

笔试面试同时被 2 个专栏收录

6 篇文章

订阅专栏

算法、数据结构

3 篇文章

订阅专栏

本文深入探讨了不同算法的时间复杂度，包括斐波那契数列的递归与迭代实现，以及各种常见算法如线性搜索、二分搜索、嵌套循环、对数时间复杂度和nlogn复杂度的详细解释。通过具体示例，文章展示了如何评估算法效率，为读者提供了优化算法性能的有效策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

在程序中，假设每个分号代表执行一步。

public class Main {
	
	/* 0 1 2 3 4 5
	 * 0 1 1 2 3 5 8 13 ....
	 */
	
	// O(2^n)
	public static int fib1(int n) {
		if (n <= 1) return n;
		return fib1(n - 1) + fib1(n - 2);
	}
	
	// O(n)
	public static int fib2(int n) {
		if (n <= 1) return n;
		
		int first = 0;
		int second = 1;
		for (int i = 0; i < n - 1; i++) {
			int sum = first + second;
			first = second;
			second = sum;
		}
		return second;
	}
	
	public static int fib3(int n) {
		if (n <= 1) return n;
		
		int first = 0;
		int second = 1;
		while (n-- > 1) {
			second += first;
			first = second - first;
		}
		return second;
	}
	

	public static void main(String[] args) {
		int n = 12;
		
		System.out.println(fib2(n));
		System.out.println(fib3(n));
		
//		TimeTool.check("fib1", new Task() {
//			public void execute() {
//				System.out.println(fib1(n));
//			}
//		});
//		
//		TimeTool.check("fib2", new Task() {
//			public void execute() {
//				System.out.println(fib2(n));
//			}
//		});
	}
	
	public static void test1(int n) {
		// 汇编指令
		
		// 1
		if (n > 10) { 
			System.out.println("n > 10");
		} else if (n > 5) { // 2
			System.out.println("n > 5");
		} else {
			System.out.println("n <= 5"); 
		}
		
		// 1 + 4 + 4 + 4
		for (int i = 0; i < 4; i++) {
			System.out.println("test");
		}
		
		// 140000
		// O(1)
		// O(1)
	}

	public static void test2(int n) {
		// O(n)
		// 1 + 3n
		for (int i = 0; i < n; i++) {
			System.out.println("test");
		}
	}

	public static void test3(int n) {
		// 1 + 2n + n * (1 + 3n)
		// 1 + 2n + n + 3n^2
		// 3n^2 + 3n + 1
		// O(n^2)
		
		// O(n)
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				System.out.println("test");
			}
		}
	}

	public static void test4(int n) {
		// 1 + 2n + n * (1 + 45)
		// 1 + 2n + 46n
		// 48n + 1
		// O(n)
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < 15; j++) {
				System.out.println("test");
			}
		}
	}

	public static void test5(int n) {
		// 8 = 2^3
		// 16 = 2^4
		
		// 3 = log2(8)
		// 4 = log2(16)
		
		// 执行次数 = log2(n)
		// O(logn)
		while ((n = n / 2) > 0) {
			System.out.println("test");
		}
	}

	public static void test6(int n) {
		// log5(n)
		// O(logn)
		while ((n = n / 5) > 0) {
			System.out.println("test");
		}
	}

	public static void test7(int n) {
		// 1 + 2*log2(n) + log2(n) * (1 + 3n)
		
		// 1 + 3*log2(n) + 2 * nlog2(n)
		// O(nlogn)
		for (int i = 1; i < n; i = i * 2) {
			// 1 + 3n
			for (int j = 0; j < n; j++) {
				System.out.println("test");
			}
		}
	}

	public static void test10(int n) {
		// O(n)
		int a = 10;
		int b = 20;
		int c = a + b;
		int[] array = new int[n];
		for (int i = 0; i < array.length; i++) {
			System.out.println(array[i] + c);
		}
	}
}

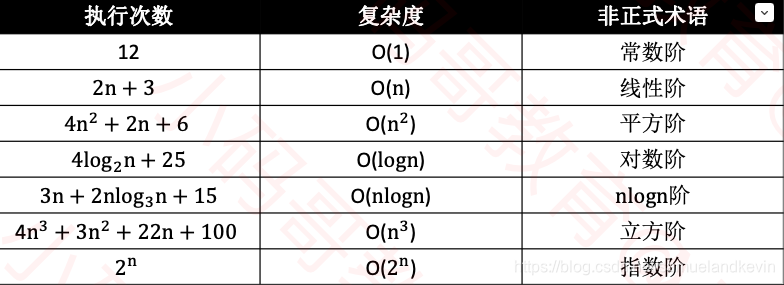
在这里插入图片描述