矩阵乘法、分解

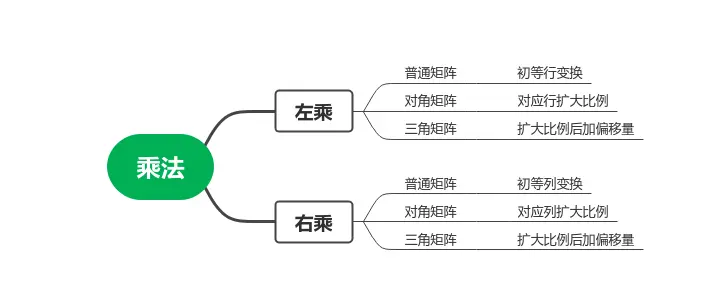
矩阵乘法

左乘是更普遍的方式。

左行右列：
初等阵 $P$ 左乘 $A$ 有 $PA$，相当于对 $A$ 按照 $P$ 的行元素，做了一次初等行变换；
初等阵 $Q$ 右乘 $A$ 有 $AQ$，相当于对 $A$ 按照 $Q$ 的列元素，做了一次初等列变换。

对角矩阵相乘，对每个行（列）都进行缩放。
三角矩阵相乘，对每个行（列）都进行缩放且有相应偏移（偏移为非对角元素作用的效果）。用图像表示为：右乘上三角矩阵，相当于图像往右上偏移；右乘下三角矩阵，相当于图像往左下偏移。

例如，矩阵A和向量B相乘为矩阵C $$\left[\begin{array}{cc}1& 2\\ 2& 0\end{array}\right]\times \left[\begin{array}{c}1\\ 2\end{array}\right]=\left[\begin{array}{c}5\\ 2\end{array}\right]$$
可以理解为将 B 视为二维空间中一个箭头，被左乘矩阵后，变成矩阵C。如果B是矩阵，则将B视为多个列向量进行转化。

$$\left[\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2}\end{array}\right]\times \left[\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right]=\left[\begin{array}{ccc}2/\sqrt{2}& 4/\sqrt{2}& 6/\sqrt{2}\\ 0& 0& 0\end{array}\right]$$矩阵相乘几何意义：右侧矩阵中的每一个列向量变换到左边矩阵中的每一行行向量为基底的空间中。数据点 $(2/\sqrt{2},0)$ $(4/\sqrt{2},0)$ $(6/\sqrt{2},0)$ 是$(1,1)$ $(2,2)$ $(3,3)$ 在 $(1/\sqrt{2},1/\sqrt{2})$ $(-1/\sqrt{2},1/\sqrt{2})$ 为基的坐标。其实就是矩阵的乘法法则推导出来的表达方式。

---

矩阵求逆

有分块矩阵$\left[\begin{array}{cc}A& B\\ 0& C\end{array}\right]$，逆为$\left[\begin{array}{cc}{A}^{-1}& -A^{-1}B{C}^{-1}\\ 0& C^{-1}\end{array}\right]$

---

矩阵特征

特征表示能代表物体的属性。矩阵的特征值和特征向量。
$$Ax=\lambda x$$
该式子表明，向量 $x$ 在 $A$ 基底的空间变换，等价于其单独 $\lambda$ 倍的变换。满足这一性质的向量 $x$ 就属于矩阵 $A$ 的特征向量，而 $\lambda$ 属于对应的特征值。可以视为复杂的矩阵变换转换到简单的数乘计算。

矩阵是对称的，特征向量全都是正交的

特征分解（谱分解）

$$\begin{array}{c}A[x_1,x_2,\cdots x_n]=[{\lambda }_1{x}_1,{\lambda }_2{x}_2,\cdots ,{\lambda }_n{x}_n]\\ A[x_1,x_2,\cdots x_n]=\left[x_1,x_2,\cdots ,x_n\right]\cdot \text{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)\\ A=\left[x_1,x_2,\cdots ,x_n\right]\cdot \text{diag}({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)\cdot [x_1,x_2,\cdots x_i{]}^T\end{array}$$

性质

特征值的和等于迹，特征值的积等于行列式。

---

矩阵分解

矩阵分解就是将矩阵组合的方式逆过来，矩阵的组合、分解类似于乘法除法。

特征分解（谱分解）

---

奇异值分解（Singular Value Decomposition）

定义：设矩阵 $A\in C_r^{m\times n}$ ，${\lambda }_i$ 是 $A{A}^H(A^{H}A)$ 的非零特征值，则称 ${\sigma }_i=\sqrt{{\lambda }_i}$ 为 $A$ 的奇异值，$i=1,2,\cdots ,r$
定理：设矩阵 $A\in C_r^{m\times n}$ ，则存在 $U\in U^{m\times m}$，$V\in U^{n\times n}$，使得 $A=U\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]V^H$，其中 $\Delta =diag[{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_r]$， ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_r$ 为 $A$ 的奇异值。
证明：因为 $A{A}^H$ 是正规阵，所以存在 $U\in U^{m\times m}$ ，使得$$U^{H}A{A}^{H}U=diag[{\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_r^2,0,\cdots ,0]=\left[\begin{array}{cc}\Delta {\Delta }^H& 0\\ 0& 0\end{array}\right]$$
且 ${\sigma }_1^2\ge {\sigma }_2^2\ge \cdots \ge {\sigma }_r^2$
其中 $\Delta =diag[{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_r]$。设 $U=[\begin{array}{cc}{U}_1& U_2\end{array}]$，则$$\begin{array}{rl}{U}^{H}A{A}^{H}U& =\left[\begin{array}{c}{U}_1^H\\ U_2^H\end{array}\right]A{A}^H\left[\begin{array}{cc}{U}_1& U_2\end{array}\right]\\ & =\left[\begin{array}{c}{U}_1^H\\ U_2^H\end{array}\right]\left[\begin{array}{cc}A{A}^H{U}_1& A{A}^H{U}_2\end{array}\right]\\ & =\left[\begin{array}{cc}{U}_1^{H}A{A}^H{U}_1& U_1^{H}A{A}^H{U}_2\\ U_2^{H}A{A}^H{U}_1& U_2^{H}A{A}^H{U}_2\end{array}\right]\\ & =\left[\begin{array}{cc}\Delta {\Delta }^H& 0\\ 0& 0\end{array}\right]\end{array}$$故有$$\begin{array}{rl}{U}_1^{H}A{A}^H{U}_1& =\Delta {\Delta }^H\\ U_1^{H}A{A}^H{U}_2& =0\\ U_2^{H}A{A}^H{U}_1& =0\\ U_2^{H}A{A}^H{U}_2& =0\end{array}$$令 $V_1=A^H{U}_1{\Delta }^{-H}$，则 $V_1^H{V}_1={\Delta }^{-1}{U}_1^{H}A{A}^H{U}_1{\Delta }^{-H}$，由 $U_1^{H}A{A}^H{U}_1=\Delta {\Delta }^H$ 得$$V_1^H{V}_1=E_r$$所以 $V_1$ 为次酉阵，即 $V_1\in U_r^{n\times r}$，故存在 $V_2\in U_{n-r}^{n\times (n-r)}$，使得 $V=[\begin{array}{cc}{V}_1& V_2\end{array}]\in U^{n\times n}$，所以$$U^{H}AV=\left[\begin{array}{c}{U}_1^H\\ U_2^H\end{array}\right]A[\begin{array}{cc}{V}_1& V_2\end{array}]=\left[\begin{array}{cc}{U}_1^{H}A{V}_1& U_1^{H}A{V}_2\\ U_2^{H}A{V}_1& U_2^{H}A{V}_2\end{array}\right]$$由 $U_1^{H}A{A}^H{U}_1=\Delta {\Delta }^H$ 得$$U_1^{H}A{V}_1=U_1^{H}A{A}^H{U}_1{\Delta }^{-H}=\Delta$$由 $U_2^{H}A{A}^H{U}_2=(A^H{U}_2{)}^H(A^H{U}_2)=0$ 得$$A^H{U}_2=0，U_2^{H}A=0$$所以 $U_2^{H}A{V}_1=0，U_2^{H}A{V}_2=0$。又因为$$V_1=A^H{U}_1{\Delta }^{-H}\Rightarrow V_1{\Delta }^H=A^H{U}_1\Rightarrow U_1^{H}A=\Delta V_1^H$$所以 $U_1^{H}A{V}_2=\Delta V_1^H{V}_2=0$。故 $U^{H}AV=\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]$，即 $A=U\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]V^H$。

分解步骤

• 求出 $A{A}^H(A^{H}A)$ 全部非零特征值 ${\lambda }_i$，记 $\Delta =diag[{\sigma }_1,{\sigma }_2,\cdots ,{\sigma }_r]$，且 ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge {\sigma }_r$ 为 $A$ 的正奇异值。
• 求酉矩阵 $U\in U^{m\times m}(V\in V^{n\times n})$，使得$$\begin{gathered} U^{H}A{A}^{H}U=diag[{\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_r^2,0,\cdots ,0] \\ (V^H{A}^{H}AV=diag[{\sigma }_1^2,{\sigma }_2^2,\cdots ,{\sigma }_r^2,0,\cdots ,0]) \end{gathered}$$
• 设 $U=[\begin{array}{cc}{U}_1& U_2\end{array}](V=[\begin{array}{cc}{V}_1& V_2\end{array}])$，其中 $U_1(V_1)$ 为 $U(V)$ 的前 $r$ 列，令 $V_1=A^H{U}_1{\Delta }^{-H}(U_1=A{V}_1{\Delta }^{-1})$，则 $V_1(U_1)$ 为次酉阵，求 $V_2\in U_{n-r}^{n\times (n-r)}(U_2\in U_{m-r}^{m\times (m-r)})$，使得 $V=[\begin{array}{cc}{V}_1& V_2\end{array}]\in U^{n\times n}(U=[\begin{array}{cc}{U}_1& U_2\end{array}]\in U^{m\times m})$。
• $A=U\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]V^H$

几何意义

$\Delta$ 视为放缩矩阵，$U$ 和 $V$ 视为旋转矩阵。
因此，对于 $M=AN$ 和 $A=U\Delta V^H$ 可以直观的解释为一个图像 $N$ 经过 $A$ 变换成另一个图像 $M$ 的过程，首先经过 $V^H$ 的旋转，再经过 $\Delta$ 的放缩，最后在经过 $U$ 的旋转得到最终的图像。

用途

可以将矩阵归一化，归一化之前的矩阵为
$$A=U\left[\begin{array}{cc}\Delta & 0\\ 0& 0\end{array}\right]V^H$$
归一化之后的矩阵满足
$$A^{\prime }=U{V}^H$$

---

QR 分解

紫薯布丁

---

Cholesky 分解

紫薯布丁

---