主成分分析法(PCA)

主成分分析法

主成分分析也称主分量分析，旨在利用降维的思想，把多指标转化为少数几个综合指标。在实证问题研究中，为了全面、系统地分析问题，我们必须考虑众多影响因素。这些涉及的因素一般称为指标，在多元统计分析中也称为变量。因为每个变量都在不同程度上反映了所研究问题的某些信息，并且指标之间彼此有一定的相关性，因而所得的统计数据反映的信息在一定程度上有重叠。在用统计方法研究多变量问题时，变量太多会增加计算量和增加分析问题的复杂性，人们希望在进行定量分析的过程中，涉及的变量较少，得到的信息量较多。主成分分析正是适应这一要求产生的，是解决这类题的理想工具。

主成分分析法是一种数学变换的方法, 它把给定的一组相关变量通过线性变换转成另一组不相关的变量，这些新的变量按照方差依次递减的顺序排列。在数学变换中保持变量的总方差不变，使第一变量具有最大的方差，称为第一主成分，第二变量的方差次大，并且和第一变量不相关，称为第二主成分。依次类推，I个变量就有I个主成分。

这种方法避免了在综合评分等方法中权重确定的主观性和随意性，评价结果比较符合实际情况；同时，主成份分量表现为原变量的线性组合，如果最后综合指标包括所有分量，则可以得到精确的结果，百分之百地保留原变量提供的变差信息，即使舍弃若干分量，也可以保证将85％以上的变差信息体现在综合评分中，使评价结果真实可靠。是在实际中应用得比较广的一种方法。由于其第一主成份（因子）在所有的主成分中包含信息量最大，很多学者在研究综合评价问题时常采用第一主成分来比较不同实体间的差别。综上所述，该方法的优点主要体现在两个方面：1.权重确定的客观性；2.评价结果真实可靠。

1．主成分分析的基本原理
主成分分析：把原来多个变量划为少数几个综合指标的一种统计分析方法，是一种降维处理技术。）

记原来的变量指标为x1，x2，…，xP，它们的综合指标——新变量指标为z1，z2，…，zm（m≤p），则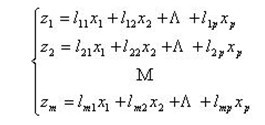


z1，z2，…，zm分别称为原变量指标x1，x2，…，xP的第一，第二，…，第m主成分，在实际问题的分析中，常挑选前几个最大的主成分。

① zi与zj（i≠j；i，j=1，2，…，m）相互无关；
② z1是x1，x2，…，xP的一切线性组合中方差最大者，z2是与z1不相关的x1，x2，…，xP的所有线性组合中方差最大者；……；zm是与z1，z2，……，zm－1都不相关的x1，x2，…，xP的所有线性组合中方差最大者。

 

2. 主成分分析的计算步骤
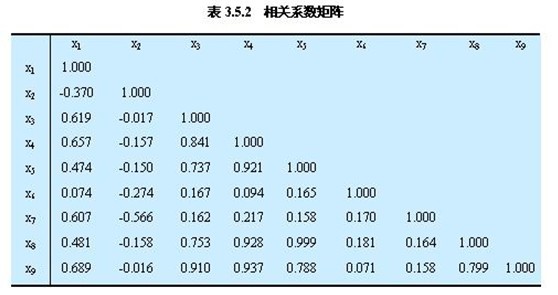
① 计算相关系数矩阵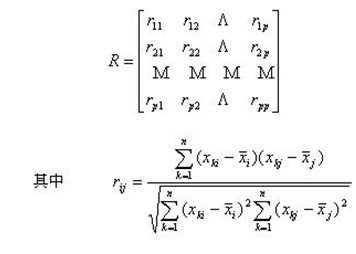


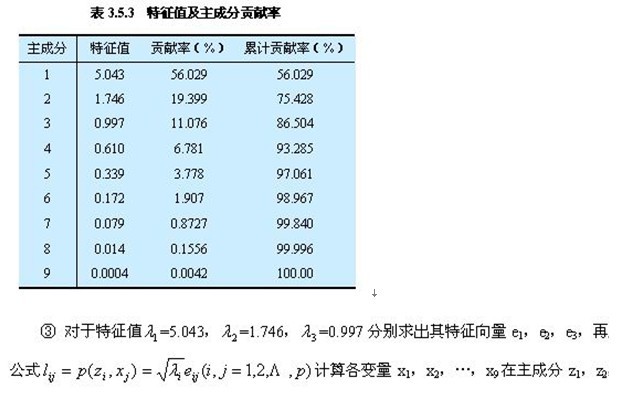
② 计算特征值与特征向量


③ 计算主成分贡献率及累计贡献率


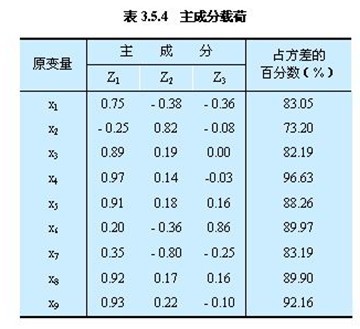
④ 计算主成分载荷

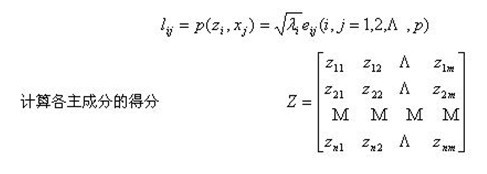
主成分分析方法（举例）

 

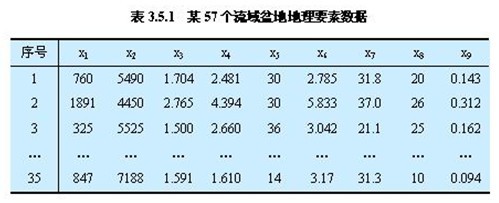
3. 主成分分析方法应用实例 1) 实例1: 流域系统的主成分分析（张超，1984） 表3.5.1（点击显示该表）给出了某流域系统57个流域盆地的9项变量指标。其中，x1代表流域盆地总高度（m），x2代表流域盆地山口的海拔高度（m），x3代表流域盆地周长（m），x4代表河道总长度（m），x5代表河道总数，x6代表平均分叉率，x7代表河谷最大坡度（度），x8代表河源数， x9代表流域盆地面积（km2）。 注：表中数据详见书本87和88页。 (1) 分析过程： ① 将表3.5.1中的原始数据作标准化处理，然后将它们代入相关系数公式计算，得到相关系数矩阵（表3.5.2）。 ② 由相关系数矩阵计算特征值，以及各个主成分的贡献率与累计贡献率（见表3.5.3）。由表3.5.3可知，第一，第二，第三主成分的累计贡献率已高达86.5%，故只需求出第一、第二、第三主成分z1，z2，z3即可。 z3上的载荷