【算法集训专题攻克篇】第二十一篇之堆-优快云博客

这篇博客探讨了在算法学习中的二叉搜索树和堆的应用。通过逆序中序遍历解决二叉搜索树中找到所有大于等于当前节点值的节点之和问题，实现高效解决方案。强调了算法在编程中的重要性，并鼓励读者不断探索和提升算法技能。

《算法集训传送门》

👉引言

在这里插入图片描述

	铭记于心
	🎉✨🎉我唯一知道的，便是我一无所知🎉✨🎉

💖 ❄️我们的算法之路❄️💖

众所周知，作为一名合格的程序员，算法能力是不可获缺的，并且在算法学习的过程中我们总是能感受到算法的✨魅力✨。
☀️🌟短短几行代码，凝聚无数前人智慧；一个普通循环，即是解题之眼🌟☀️
💝二分，💝贪心，💝并查集，💝二叉树，💝图论，💝深度优先搜索(dfs)，💝宽度优先搜索（bfs），💝数论，💝动态规划等等， 路漫漫其修远兮，吾将上下而求索！希望在此集训中与大家共同进步，有所收获！！！🎉🎉🎉

今日主题：堆

👉⭐️第一题💎

✨题目

剑指 Offer II 054. 所有大于等于节点的值之和

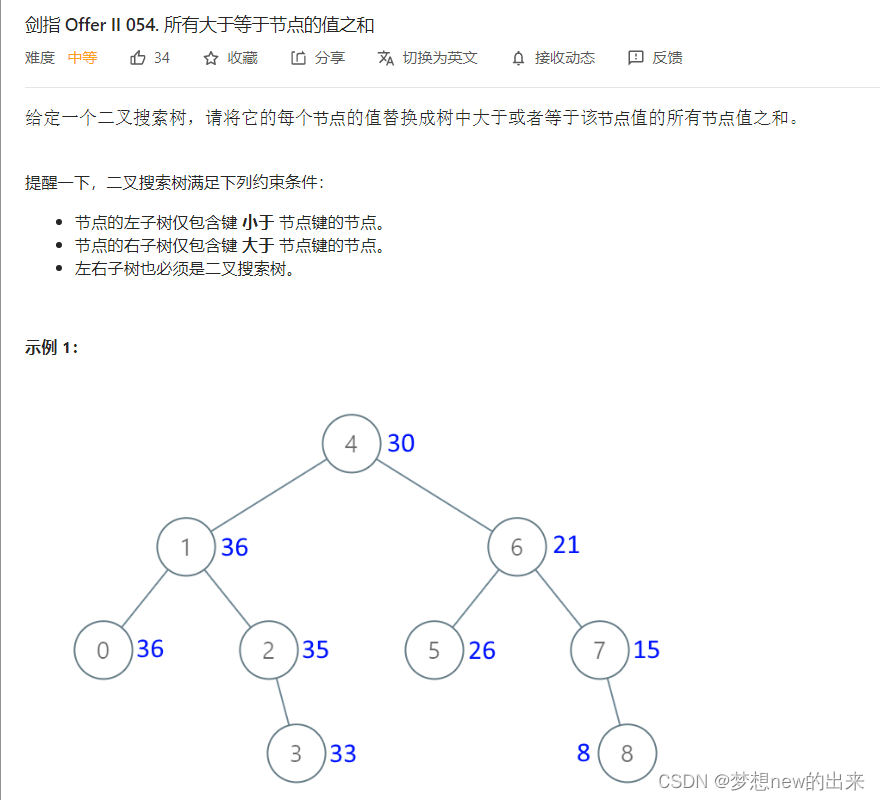
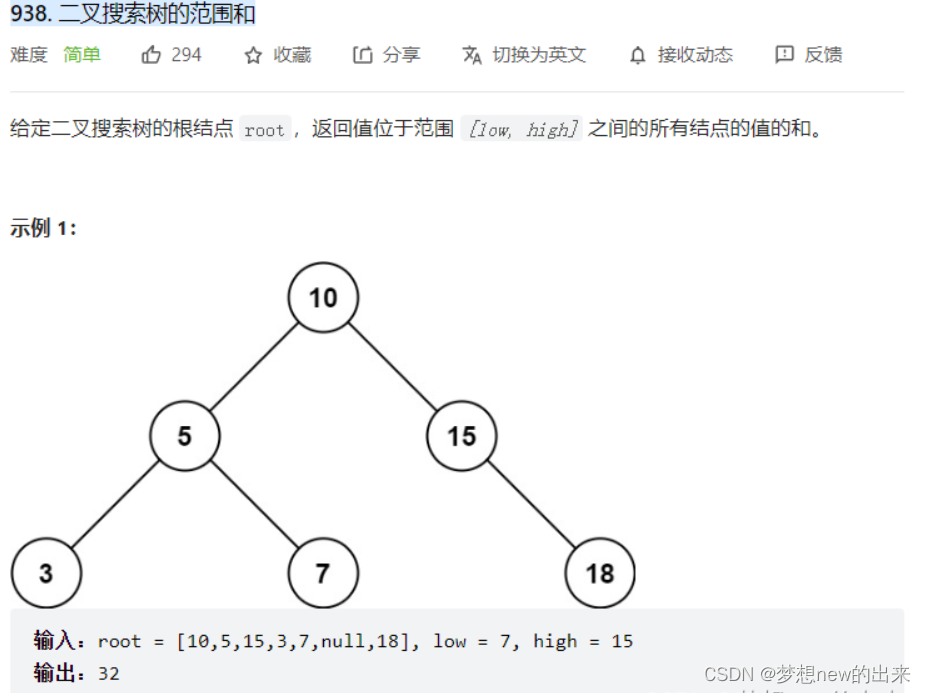
在这里插入图片描述

关于二叉搜索树，相信大家并不陌生，就是 root节点左边的子节点都小于该root 的value，而右节点都大于value，有一道简单的二叉搜索题，可以看下图：

对于本文首题来说，首先是
暴力原则上都是可行的，暴力遍历每个节点，然后以此节点为评判标准，再去搜索二叉树子节点，找遍所有满足条件的节点，最终累加替换，可以用记忆化搜索优化，但时间复杂度较高(O(n2))
根据二叉搜索树的特性可知，其顺序中序遍历可以得到递增节点，那么对于每个节点，从后往前累加，就是所有大于等于该节点的和了，也就是使用逆序中序遍历，时间复杂度为 O(n)，相对来说快很多

✨代码：

class Solution {
    private int sum;// 记录比当前节点大的节点和
    public TreeNode convertBST(TreeNode root) {
        dfs(root);// 进行深度优先遍历
        return root; // 返回树的根节点
    }
    private void dfs(TreeNode root){
        // 当 root 为空，则结束递归
        if(root == null) return;
        // 遍历右节点
        dfs(root.right);
        // 将当前节点的值加上前面比它大的节点和
        int val = root.val;
        root.val += sum;
        // 更新节点和
        sum += val;
        // 遍历左节点
        dfs(root.left);
    }
}