题目:123.买卖股票的最佳时机III
题目链接:123. 买卖股票的最佳时机 III - 力扣(Leetcode)
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。 随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1] 输出:0
提示:
1 <= prices.length <= 105
0 <= prices[i] <= 105
思路:最多两笔交易,意思是可以买卖一次,可以买卖两次,也可以不买卖
1.dp数组的含义
总共有四个状态:
没有操作 dp[i][0]
第一次持有股票 dp[i][1]
第一次不持有股票 dp[i][2]
第二次持有股票 dp[i][3]
第二次不持有股票dp[i][4]
2.递推公式
dp[i][1] = max(dp[i-1][0] - prices[i], dp[i - 1][1]);
dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);3.dp数组初始化
dp[0][0]=0;
dp[0][1]=-prices[0];
dp[0][2]=0;
dp[0][3]=-prices[0];
dp[0][4]=0;4.遍历顺序
从前往后
5.举例推导dp数组
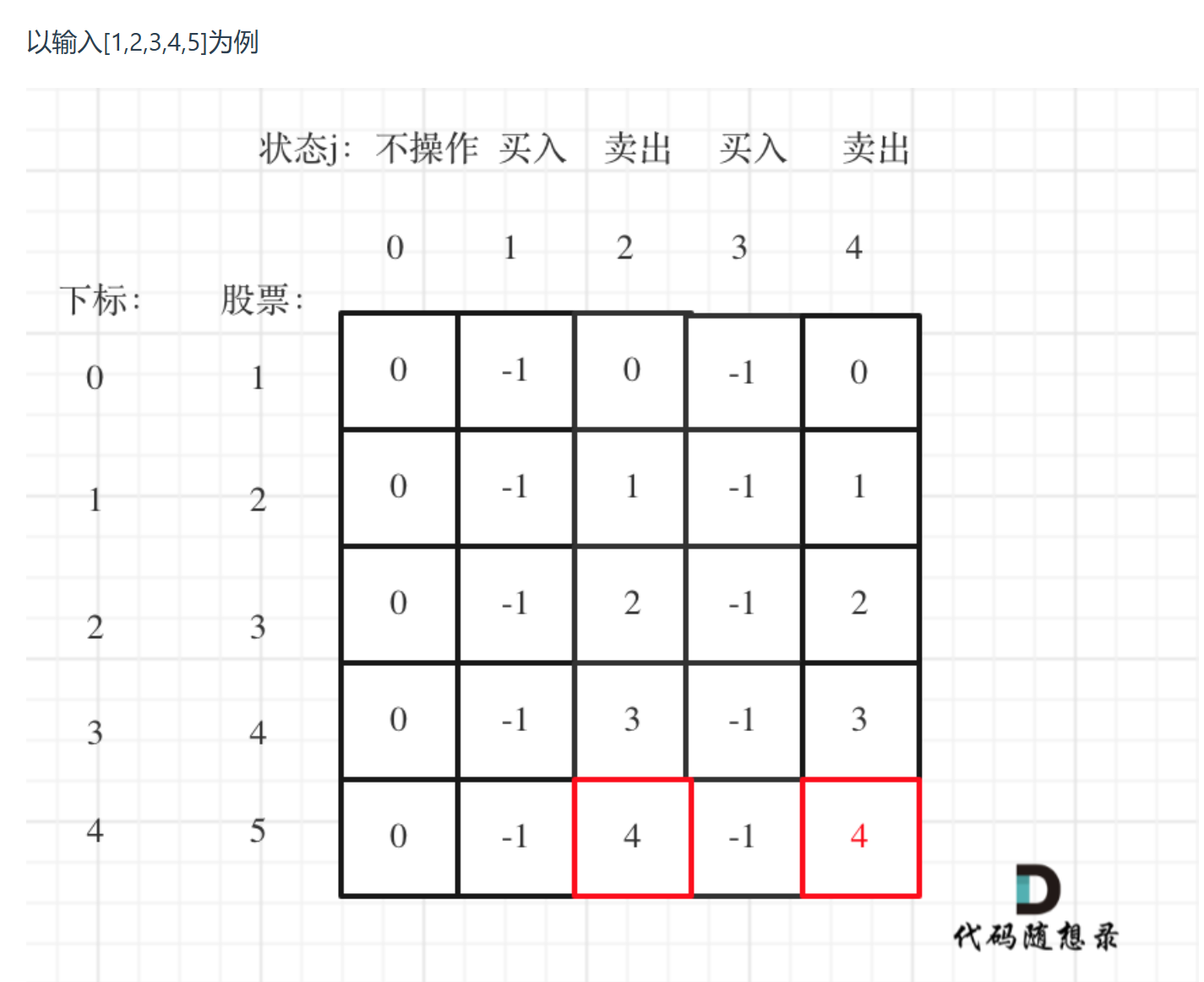
// 版本一
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0;
vector<vector<int>> dp(prices.size(), vector<int>(5, 0));
dp[0][1] = -prices[0];
dp[0][3] = -prices[0];
for (int i = 1; i < prices.size(); i++) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4];
}
};
时间复杂度:O(n)
空间复杂度:O(n × 5)题目:188.买卖股票的最佳时机IV
题目链接:188. 买卖股票的最佳时机 IV - 力扣(Leetcode)
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
0 <= k <= 100
0 <= prices.length <= 1000
0 <= prices[i] <= 1000
思路:最多k次交易
和123.买卖股票的最佳时机类似。
将状态分为奇偶
奇状态的递推公式为
if(j%2==1) dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]-prices[i]);偶状态的递推公式为
if(j%2==0) dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]+prices[i]);dp数组的初始化
奇状态的初始化:
if(i%2==1)dp[0][i]=-prices[0];偶状态的初始化:
if(i%2==0)dp[0][i]=0;具体代码如下:
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if(k==0)return 0;
vector<vector<int>> dp(prices.size(),vector<int>(2*k+1));
dp[0][0]=0;
for(int i=1;i<2*k+1;i++){
if(i%2==1)dp[0][i]=-prices[0];
if(i%2==0)dp[0][i]=0;
}
for(int i=1;i<prices.size();i++){
for(int j=1;j<2*k+1;j++){
if(j%2==1) dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]-prices[i]);
if(j%2==0) dp[i][j]=max(dp[i-1][j],dp[i-1][j-1]+prices[i]);
}
}
// for(int i=1;i<prices.size();i++){
// for(int j=1;j<2*k+1;j++){
// cout<<dp[i][j]<<" ";
// }
// cout<<endl;
// }
return dp[prices.size()-1][2*k];
}
};




 文章讲述了如何使用动态规划算法解决LeetCode上的123和188题,即在给定交易限制下找到股票买卖的最佳时机以获取最大利润。通过建立状态转移方程,分析不同交易次数下的最优策略,实现求解最大利润的方法。
文章讲述了如何使用动态规划算法解决LeetCode上的123和188题,即在给定交易限制下找到股票买卖的最佳时机以获取最大利润。通过建立状态转移方程,分析不同交易次数下的最优策略,实现求解最大利润的方法。
















 2001
2001

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








