吴恩达机器学习第三章线性代数回顾学习笔记

matrix：矩阵

vector：向量

vector: an n *1matrix;

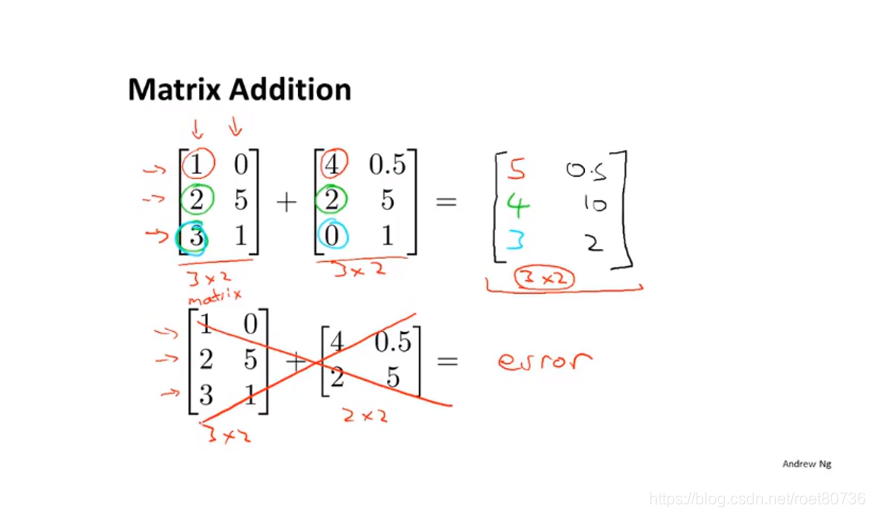
矩阵的加法：只有相同维度的矩阵才能相加

 

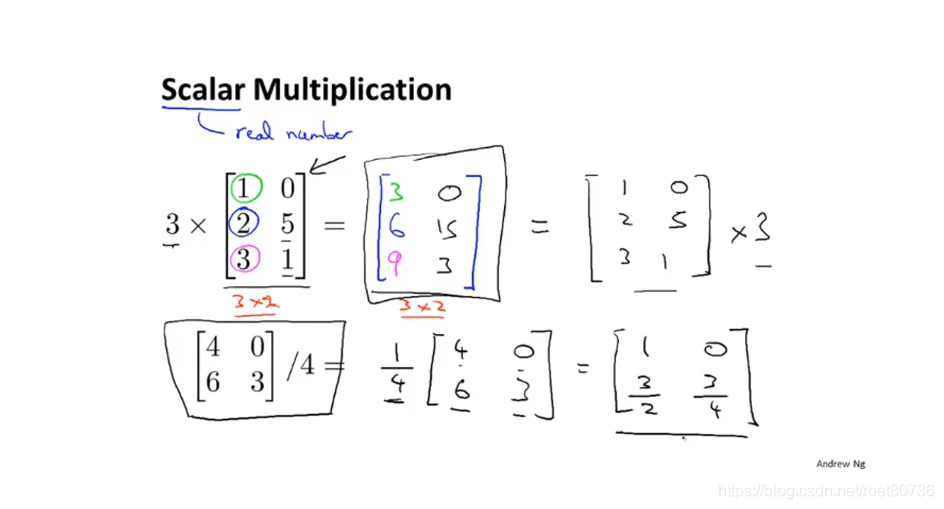
矩阵的乘法和除法：

 

两个矩阵的乘法：

 

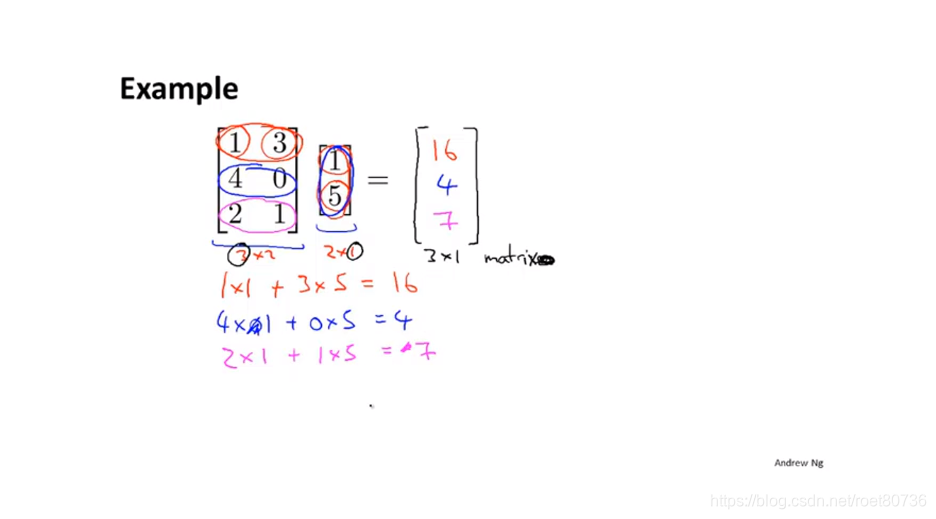
m×n矩阵 乘以 n×o矩阵 = m×o矩阵

矩阵的乘法不满足交换律：A×B ≠ B×A

矩阵的乘法满足结合律：A×B×C = A×（B×C）

单位矩阵： 在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1，这种矩阵被称为单位矩阵。它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。

 

任何矩阵与单位矩阵相乘等于自身： A ×I = I×A = A

矩阵的逆矩阵：

矩阵A乘以某个矩阵B等于单位矩阵I，那么这个矩阵B就叫做矩阵A的逆矩阵（矩阵A的行和列必须相等才有逆矩阵）

没有逆矩阵的矩阵叫做奇异矩阵或者退化矩阵；

零矩阵没有逆矩阵；

转置矩阵：

将矩阵的行列互换得到的新矩阵称为转置矩阵，转置矩阵的行列式不变。

由定义可知， 为  矩阵，则 为 矩阵。

例如， 

  

如果  阶方阵和它的转置相等 ，即 ，则称矩阵 为对称矩阵。

如果  ，则称矩阵 为反对称矩阵。