剑指 offer第11题- 旋转数组的最小数字_矩形覆盖旋转数组中的最小数字-优快云博客

本文介绍了一种在非递减排序的旋转数组中查找最小元素的高效算法，通过修改二分查找实现，时间复杂度为O(logN)，并讨论了数组元素可能重复的情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。

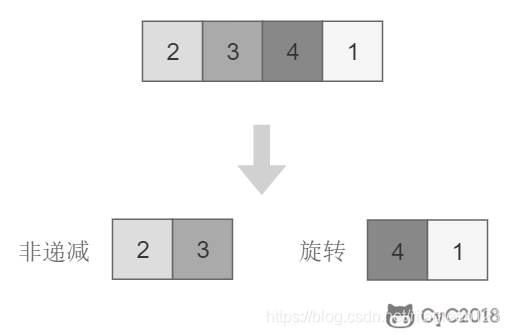
将旋转数组对半分可以得到一个包含最小元素的新旋转数组，以及一个非递减排序的数组。新的旋转数组的数组元素是原数组的一半，从而将问题规模减少了一半，这种折半性质的算法的时间复杂度为 O(logN)（为了方便，这里将 log2N 写为 logN）。
在这里插入图片描述
图片来自：https://cyc2018.github.io/CS-Notes/#/notes/剑指 Offer 题解 - 10~19?id=_102-矩形覆盖

可以把旋转数组分为一个非递减和旋转数组，非递减的第一个元素肯定小于最后一个元素，所以我们要在旋转数组里面找最小的元素。

通过修改二分查找算法进行求解（l 代表 low，m 代表 mid，h 代表 high）：

1.当 nums[m] <= nums[h] 时，表示 [m, h] 区间内的数组是非递减数组，[l, m] 区间内的数组是旋转数组，此时令 h = m；
2. 否则 [m + 1, h] 区间内的数组是旋转数组，令 l = m + 1。

import java.util.ArrayList;
public class Solution {
    public int minNumberInRotateArray(int [] array) {
        if(array.length==0){
            return 0;
        }
        int l=0,h=array.length-1;
        while(l<h){
            int m =(l+h)/2;
            if(array[m]<=array[h]){
                h=m;
            }else{
                l=m+1;
            }
        }
        return array[l];
    
    }
}

另一种情况：数组允许重复：
加一个判断，nums[l] == nums[m] == nums[h]时，在l和h之间顺序查找。

public class Solution {
    public int minNumberInRotateArray(int [] array) {
        if(array.length==0){
            return 0;
        }
        int l=0,h=array.length-1;
        while(l<h){
            int m =(l+h)/2;
            if(array[l]==array[m]&&array[m]==array[h]){
                return minNumbers(array,l,h);
            }else if(array[m]<=array[h]){
                h=m;
            }else{
                l=m+1;
            }
        }
        return array[l];
    
    }
    private int minNumbers(int[] nums,int l,int h){
        int result= nums[l];
        for(int i=l+1;i<=h;i++){
            if(result>nums[i]){
                result=nums[i];
            }
        }
        return result;
    }
}