算法工程师重生之第四十三天（图论理论基础 深搜理论基础 所有可达路径 广搜理论基础）

参考文献 代码随想录

一、图论理论基础

这一篇我们正式开始图论！

代码随想录图论中的算法题目将统一使用ACM模式，为什么要使用ACM模式

#图的基本概念

二维坐标中，两点可以连成线，多个点连成的线就构成了图。

当然图也可以就一个节点，甚至没有节点（空图）

#图的种类

整体上一般分为 有向图 和 无向图。

有向图是指 图中边是有方向的：

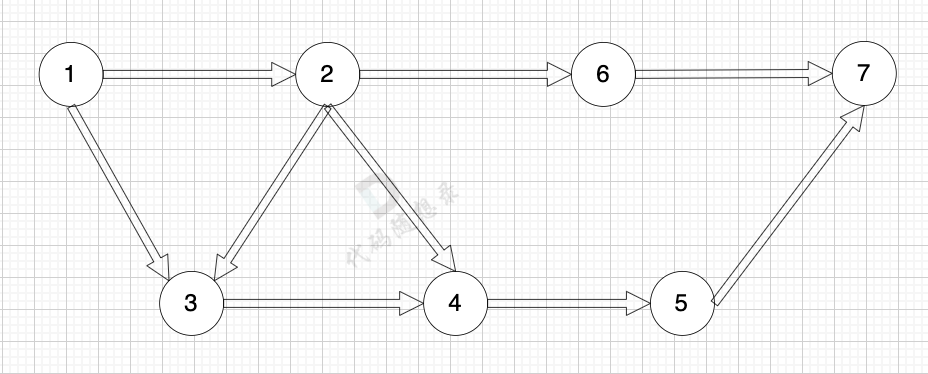
无向图是指 图中边没有方向：

加权有向图，就是图中边是有权值的，例如：

加权无向图也是同理。

#度

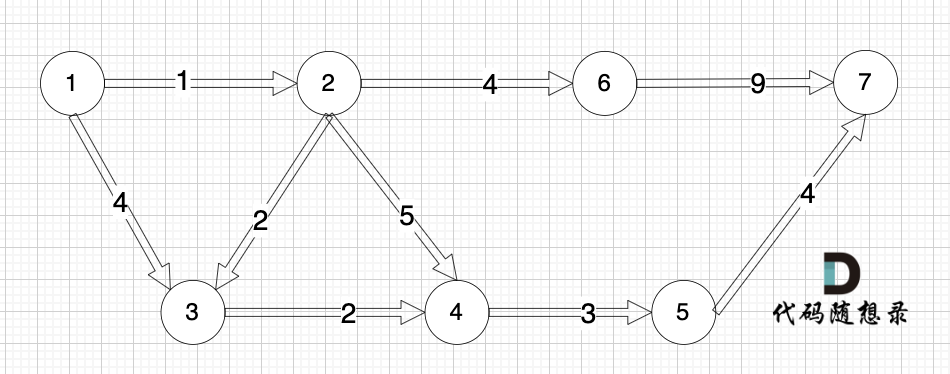
无向图中有几条边连接该节点，该节点就有几度。

例如，该无向图中，节点4的度为5，节点6的度为3。

在有向图中，每个节点有出度和入度。

出度：从该节点出发的边的个数。

入度：指向该节点边的个数。

例如，该有向图中，节点3的入度为2，出度为1，节点1的入度为0，出度为2。

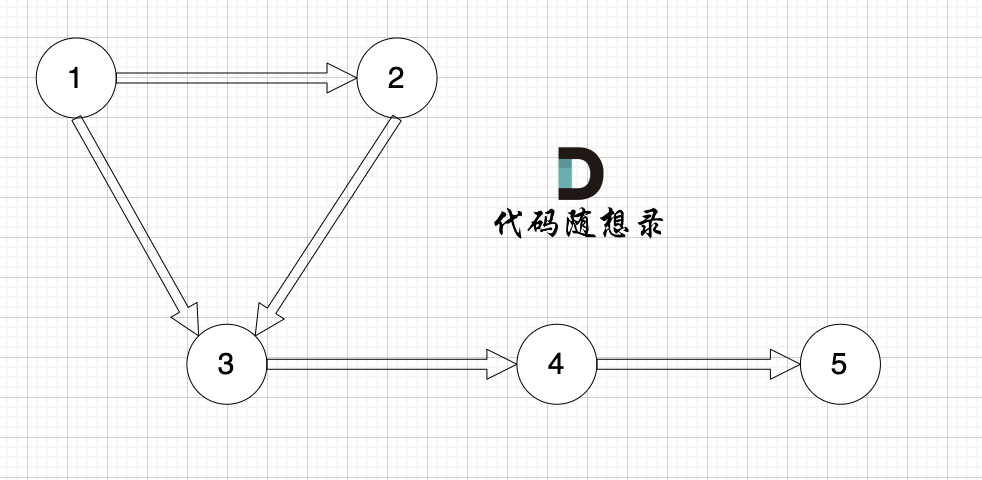
#连通性

在图中表示节点的连通情况，我们称之为连通性。

#连通图

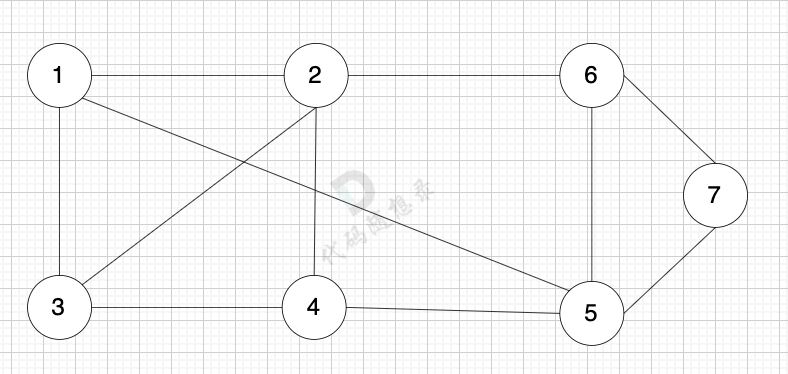
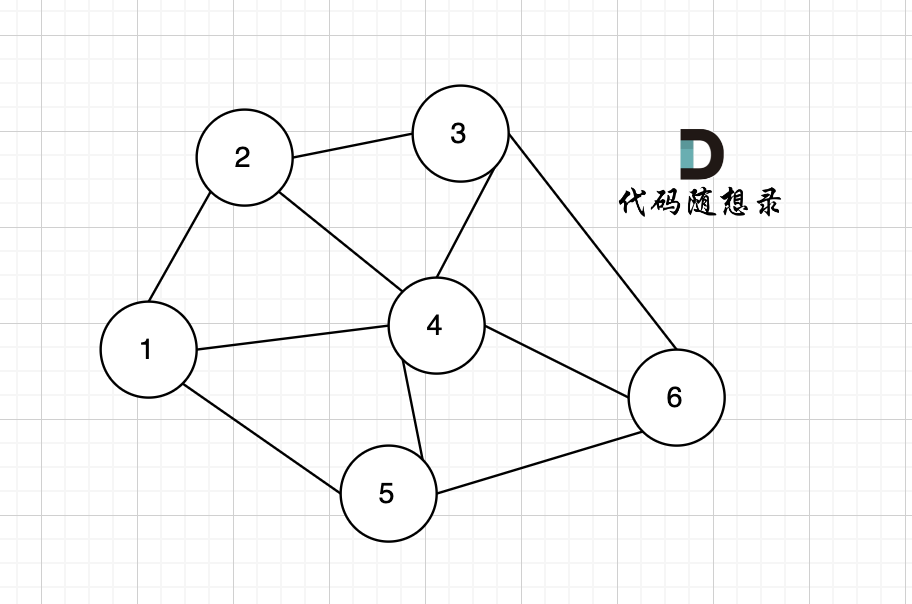
在无向图中，任何两个节点都是可以到达的，我们称之为连通图 ，如图：

如果有节点不能到达其他节点，则为非连通图，如图：

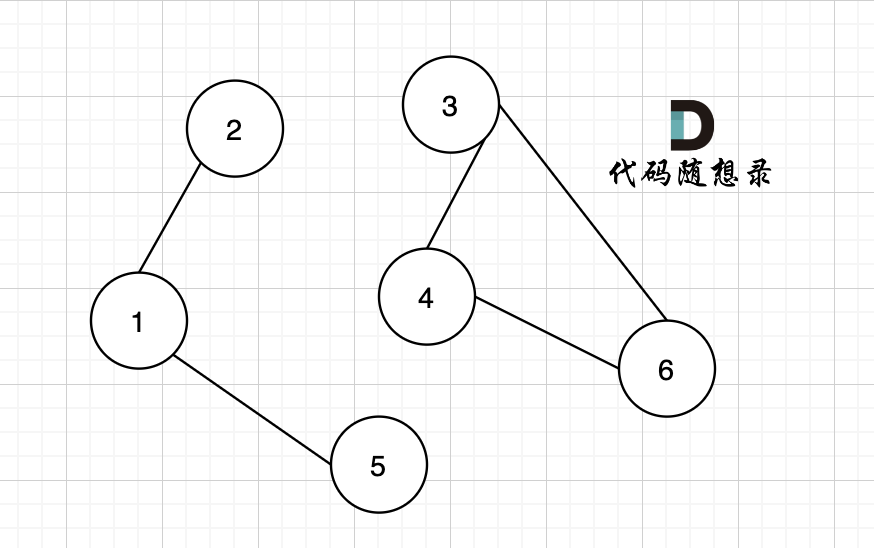
节点1 不能到达节点4。

#强连通图

在有向图中，任何两个节点是可以相互到达的，我们称之为 强连通图。

这里有录友可能想，这和无向图中的连通图有什么区别，不是一样的吗？

我们来看这个有向图：

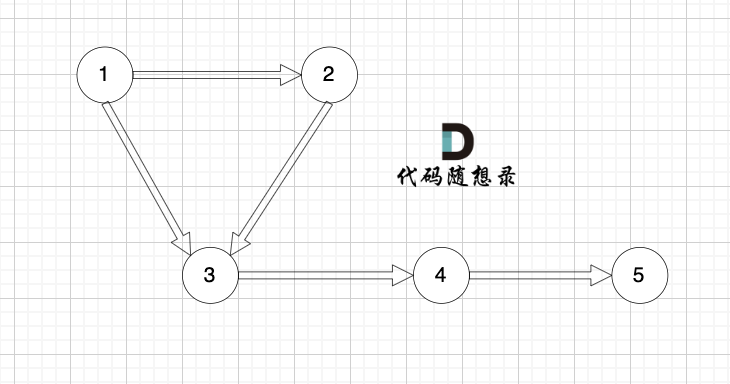
这个图是强连通图吗？

初步一看，好像这节点都连着呢，但这不是强连通图，节点1 可以到节点5，但节点5 不能到 节点1 。

强连通图是在有向图中任何两个节点是可以相互到达

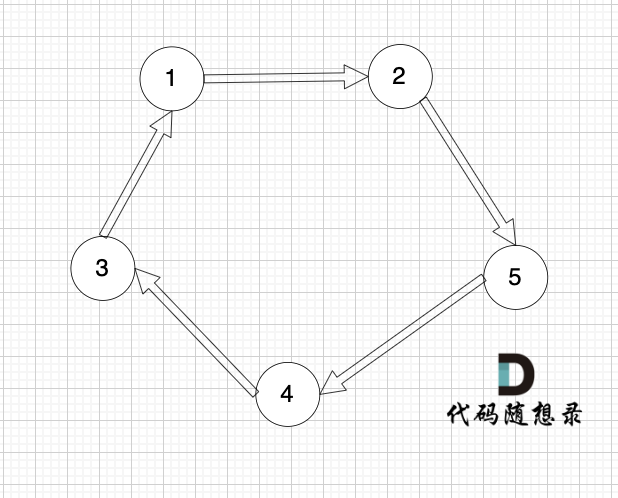
下面这个有向图才是强连通图：

#连通分量

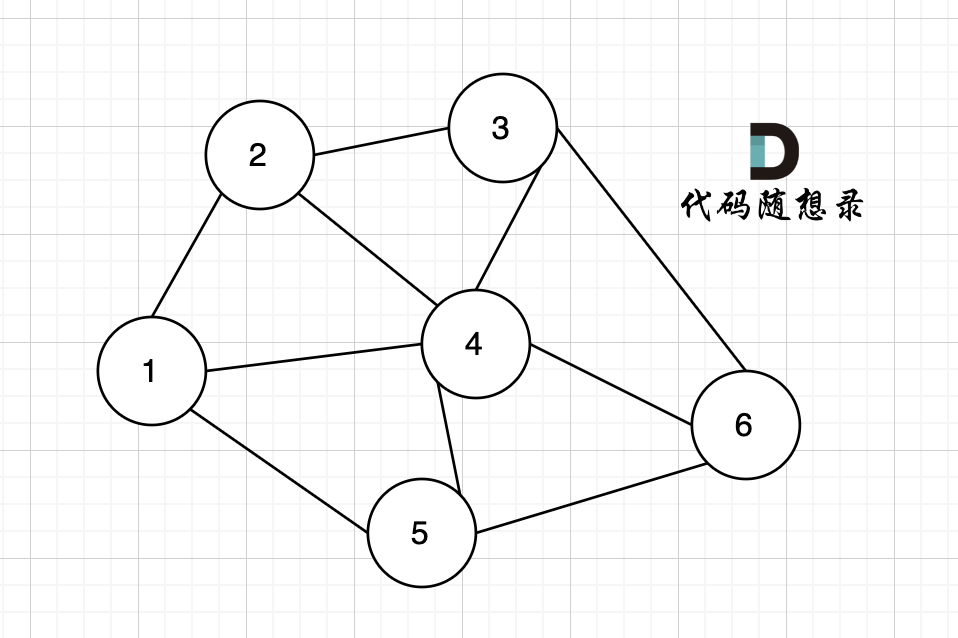
在无向图中的极大连通子图称之为该图的一个连通分量。

只看概念大家可能不理解，我来画个图：

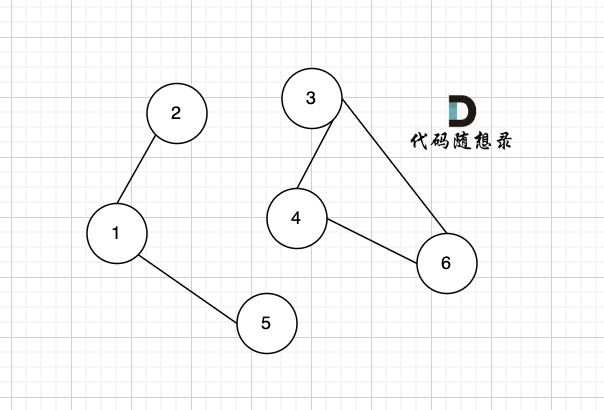
该无向图中 节点1、节点2、节点5 构成的子图就是 该无向图中的一个连通分量，该子图所有节点都是相互可达到的。

同理，节点3、节点4、节点6 构成的子图 也是该无向图中的一个连通分量。

那么无向图中 节点3 、节点4 构成的子图 是该无向图的联通分量吗？

不是！

因为必须是极大联通子图才能是连通分量，所以 必须是节点3、节点4、节点6 构成的子图才是连通分量。

在图论中，连通分量是一个很重要的概念，例如岛屿问题（后面章节会有专门讲解）其实就是求连通分量。