C语言函数详解：自定义函数、递归与经典案例-优快云博客

本文链接：https://blog.youkuaiyun.com/resetm/article/details/115769435

本文详细介绍了C语言函数的基础概念，包括函数定义、分类（库函数与自定义）、参数传递（形参与实参）、调用规则（传值与传址）、嵌套调用、链式访问以及递归函数的应用，如汉诺塔和青蛙跳台阶问题的递归与非递归解法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、函数的定义及分类

1、定义

由一个或多个语句块构成，负责完成某项特定的任务，具备相对独立性的子程序叫做函数。函数一般还有输入参数和返回值。

2、分类

（1）库函数

一些基础的功能因为需要频繁的使用，C语言就将其封装成一个个函数，来提高编程开发效率，使得语言标准化，这就是库函数。
C语言常见的库函数主要有这几个：IO函数、字符串操作函数、字符操作函数、内存操作函数、时间/日期函数、数学函数等等。使用库函数只需要记住在使用时一定要记得包含它对应的头文件，就OK了。
关于库函数的查找可以去C/C++的官网（网址）或者MSDN等等都可以。不过最好去它的官网，比较全面标准一些。

（2）自定义函数

自定义函数和库函数的最大的区别就是里面实现的功能是自己设计的，比较灵活方便。当然它也有函数名，返回值和参数。函数的组成结构如下：
函数组成结构
举个例子：求出两个数中的较大值，要求使用函数实现

#include<stdio.h>
int Max(int a,int b){
    return (a > b) ? a : b;
}
int main(){
int x = 2;
int y = 3;
int result = Max(x , y);
printf("%d\n",result);
return 0;
}

二、函数的参数

1、形参

定义函数时，函数名括号后的变量。只有在函数被调用的时候才会实例化，调用完后自动销毁。

2、实参

函数调用时，实际传给函数的参数。它可以是有确定值的常量、变量、表达式、函数等等。

三、函数的一些使用规则

1、函数调用

（1）传值调用

形参和实参具有不同的内存单元，对形参改变不会影响实参。

（2）传址调用

传递的参数是内存地址，把函数外部创建的变量地址传递给形参。通过对形参的修改就可以改变实参，这种方式让函数外部的变量和函数建立了真正的联系，可以通过函数内部变量直接操作函数外部变量。
举一个例子：交换两个变量的值

#include<stdio.h>
void swap(int * a, int * b) {
    int tmp = 0;
    tmp = *a;
    *a = *b;
    *b = tmp;
    return;
}
int main() {
    int x = 2;
    int y = 3;
    swap(&x, &y);
    printf("%d %d\n", x, y);
    return 0;
}

若是采用传值调用，无法实现这一功能，因为函数内部创建的变量函数调用结束就会销毁，并没有改变这两个值。当使用传址调用就可以轻松实现！

2、函数的嵌套调用

函数之间是可以相互组合调用的，可以实现嵌套调用，但是注意函数在定义的时候是不可以嵌套的！
举例如下：

#include<stdio.h>
void a() {
    printf("aaaa\n");
    return;
}
void b() {
    a();
    printf("bbbb\n");
    return;
}
int main() {
    b();
    return 0;
}

3、函数的链式访问

链式访问，就是把一个函数的返回值作为另一个函数的参数。这里来挖一个很有意思的东西。
这是对于标准输出printf的定义：

int printf( const char *format [, argument]… );
Return Value：Each of these functions returns the number of characters printed, or a negative value if an error occurs.（每个函数都返回打印的字符数，如果发生错误，则返回负值）

了解了这个之后，我们用printf来做一个简单的链式访问，请你猜猜下面的程序输出是什么？

#include<stdio.h>

int main() {
    printf("%d", printf("%d", printf("%d", 43)));
    return 0;
}

运行结果
不知道你猜对了吗？哈哈哈哈哈，我第一次见这个就觉得很有意思。

它是这样理解的：最里面一层输出43，是两个字符；所以中间那一层打印返回值打印一个2，这样中间一层只输出了一个字符，最外面的printf就只能打印返回值打印一个1。

4、函数的定义和声明

函数的定义就是指函数的具体实现，交代它的实现功能。

函数的声明则是对编译器说明函数的函数名，返回值和参数，具体是否创建不归声明管。函数的声明一般放在头文件（.h文件）中，出现在函数使用之前，满足先声明后使用。

若是一个函数和main函数放到了一个源文件且放到了main函数之后，那么在main函数之前一定要先声明。不过现在一般的编程都会直接把自定义函数放到main函数之前。

四、递归函数

程序调用自身的编程方式就叫做递归。

递归的主要思想就是把一个大型的复杂问题通过层层转化，变成一个规模较小的问题。
递归必须要有停下来的限制条件，且每次递归之后都会接近这个限制条件，缩小规模。

不过注意：
许多问题会采用递归的方式去解释，因为它的优点之一就是逻辑清晰，但是迭代实现往往实现效率更高。所以当一个问题非常非常复杂时，递归是远远优于其他方法的，此时它的简洁就可以弥补它所产生的开销。

这里，讲两个经典题目：汉诺塔问题和青蛙跳台阶

1、汉诺塔问题

汉诺塔来源于印度传说的一个故事，上帝创造世界时作了三个金刚石柱子，在一根柱子上从上往下，按从小到大顺序摞着64片黄金圆盘，上帝命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上，并且规定，在小圆盘上不能放大圆盘，在三根柱子之间每次只能移动一个圆盘，只能移动在最顶端的圆盘。那么，对于一个N层的汉诺塔圆盘，要将其从第一根柱子上挪到第三根上的挪动次数是多少？

（1）递归求解

解题思路：直接通过模拟汉诺塔的移动轨迹来计算移动次数是一件极其麻烦的事，所以呢我们可以先把规模放小，看一下规律：

两个盘子时
先把上面1个盘子挪到辅助柱B上，把最下面那个挪到C上，最后再把上面1个挪到C上
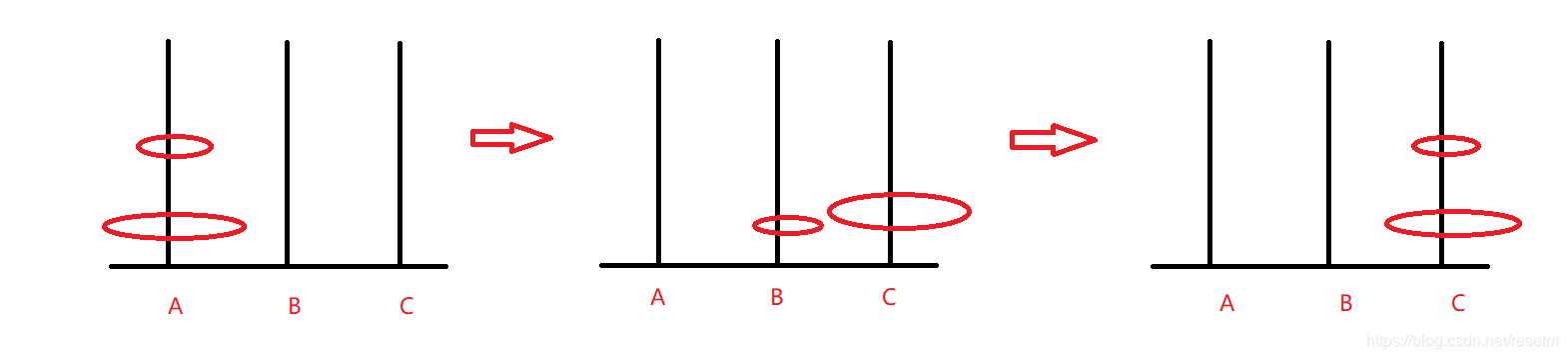
3个盘子时
先把上面的2个盘子挪到辅助柱B上，把最下面那个挪到C上，最后再把上面2个挪到C上。
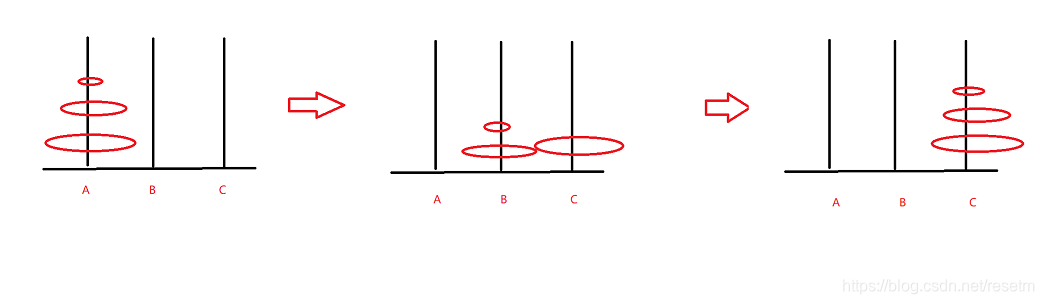
总结n个盘子
先把上面的（n-1）个盘子挪到辅助柱B上，把最下面那个挪到C上，最后再把上面(n-1)个挪到C上。下面看代码：

#include<stdio.h>

//n表示层数，a：原柱 b：目标柱 c：辅助柱
int time = 0;    //设计一个全局变量来记录移动次数
void rec_hanoi(int n, char a, char b, char c) {
	if (n >= 1) {
		rec_hanoi(n - 1, a, c, b);    //把a的n-1层移到辅助柱c上
		printf("第%d次：把第%d层圆盘从%c移到%c上\n",time+1,n,a,b );    //把a的最下面一层移到目标柱b上
		time++;
		rec_hanoi(n - 1, c, b, a);    //把辅助柱c的n-1层移到目标柱b上
	}
	return;
}
int main() {
	int n = 0;
	scanf("%d", &n);
	rec_hanoi(n, 'A', 'C', 'B');    //A为原柱，B为目标柱，C为辅助柱
	printf("%d\n",time );
	return 0;
}

（2）非递归求解

这里再写出一个非递归求次数的代码，具体思路看图，不要问我移动n层的次数公式怎么得来的哈哈哈哈，写几个小规模的出来，你也可以总结看出规律喔！（狗头）
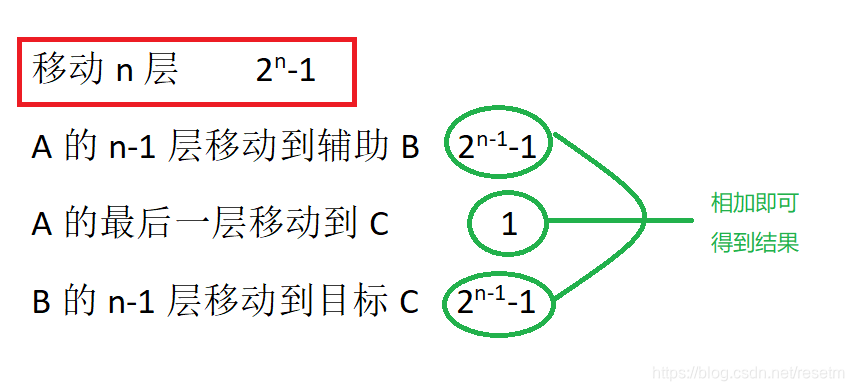非递归思路虽然不用函数也很简单，但为了逻辑更加清晰，这里采用了函数的方式实现。代码如下：

#include<stdio.h>
#include<math.h>
int no_rec_hanoi(int n) {
	//总次数就是2*((2^(n-1))-1)+1 = 2^n-2+1 = 2^n-1
	return pow(2,n)-1;    
}
int main() {
	int n = 0;
	scanf("%d", &n);
	printf("%d\n", no_rec_hanoi(n));
	return 0;
}

2、青蛙跳台阶

一只青蛙一次可以跳上一级台阶，也可以一次跳上两级台阶。那么当台阶有n级时，问青蛙有多少种跳法？

解题思路：首先像这种求可能性的问题一般都会有递推关系，就很容易想到用递归去解决。

想一下到最后一步时，要么青蛙跳一级，要么跳两级。如果设n级台阶有f(n)种跳法，若是最后一次跳了一级就有f(n-1)种跳法，若是最后一次跳了两级就有f(n-2)种跳法，对于f(n)只有这两种情况，所以f(n) = f(n-1) + f(n-2)。

推到这里是不是感觉有点熟悉？没错它的原型就是斐波那契数列，但是还有一点小小的不同：

斐波那契数列：对于起始f(0) = 0 ， f(1) = 1 ， f(2) = 1 ， f(3)开始每一项等于前两项和
青蛙跳台阶：对于起始f(0) = 1， f(1) = 1 ， f(2) = 2 ， f(3)开始每一项等于前两项和

注意到这个问题之后，就可以开始写代码了，同样用递归和非递归两种方法去解。

（1）递归求解

#include<stdio.h>

int rec_fab(int n) {
	int a = 1e9 + 7;
	if (n == 0) {
		return 1;
	}
	if (n <= 2) {
		return n;
	}
	else {
		return (rec_fab(n - 1) + rec_fab(n - 2))%a;
	}
}
int main() {
	int input = 0;
	scanf("%d", &input);
	printf("跳%d级台阶一共有%d种跳法\n", input, rec_fab(input));
}

（2）非递归求解

#include<stdio.h>

int no_rec_fab(int n) {
	int a = 1e9 + 7;
	int ret = 1;
	if (n == 0) {
		ret = 1;
	}
	else if (n <= 2) {
		ret = n;
	}
	else {
		ret = 2;
		int pre_ret = 1;    //f(n-1)
		int pre_pre_ret = 0;    //f(n-2)
		while (n > 2) {
			pre_pre_ret = pre_ret;
			pre_ret = ret;
			ret = pre_pre_ret + pre_ret;
			n--;
		}
	}
	return ret%a;
}
int main() {
	int input = 0;
	scanf("%d", &input);
	printf("跳%d级台阶一共有%d种跳法\n", input, no_rec_fab(input));
}