基于比较排序的时间复杂度下限

基于比较的排序算法的时间复杂度下限[转]

昨天下午吃完饭，正好碰到一同学，就随便聊了聊。他说刚参加完一个面试。我很感兴趣，因为下半年就该我找工作了，这方面的信息对我来说比较重要。看得出来，他有点小郁闷，说面试官是个BT。问了原因之后，我便很同意他这个观点了。面试官似乎对查找和排序很感兴趣，问的大部分都是这方面的。首先是让用n+lgn的时间复杂度求出一个无序数组的最大值和第二大值，tooooold，同学面不改色答之，然后O(n)求第k大，同学是blabla, 又出个用基数排序的，同学也答出，面试官很是欣慰。同学于是得意啦，分析其复杂度，随口一句: 这个问题用基排最好，其他基于比较的最小也得nlgn。 面试官也是随口一句：嗯，是最小nlgn，不过为什么？同学说，当时他给雷到了。说，如果让他分析一个具体的排序算法，他可能还能应付，可这么个问题，有点让他找不到北。是啊，好多时候，我们只记得结果，却忘记了得出结果的过程。

         其实这个问题也是一个toooooold的问题，好多年前就已经给计算科学家证出来了。 而且思路很简单：

比如要用基于比较的方法排序 A1,A2, A3, 其实就是找到一个两两比较序列，而这些序列都是下面这个二叉树中某一个从根到叶子的路径。

 

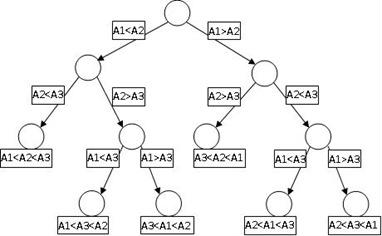
那么基于比较的排序的时间复杂度就是这颗数的深度H(N)。而且很容易知道叶子节点的个数就是N的排列 N！， 那么我们就有

                         2^H(N) >= N! > N*(N-1)*.....*(N/2) > (N/2)^(N/2)

                         H(N) > (N/2)lg(N/2) = O(nlgn)            得证