树的搜索问题2——分支界限和A*算法（多阶段图问题、人员安排问题和旅行商问题）

前言

在上一篇博客中我们简单提了一下深度优先和广度优先，然后就开始了爬山法和best-first算法。

尽管貌似我们已经说了很多了，但是我们上一篇博客都是在围绕一个问题——所有的问题都是有一个确定的解，我们是在找解出问题的路径。

但如果是一个优化解问题呢？比如在一个多阶段图中寻找从起点到终点的最短路径？
这些算法其实是不能使用的，但这一类问题却很多，我们需要给出新的算法。
（之前的算法也不是没有用，和深度优先广度优先差不多，也都是在给我们即将到来的算法做铺垫）

分支界限法

分支界限法又叫剪枝法
顾名思义，其实就是通过一种方式快速的找到一个较优化解（一般来说是爬山法），然后利用得到的界限来将一些不可能的解删除掉，减少我们的搜索时间（当前的搜索方式为best-first）

问题1，之前提到的多阶段图，这里我们需要计算从v0到v3的最短路径

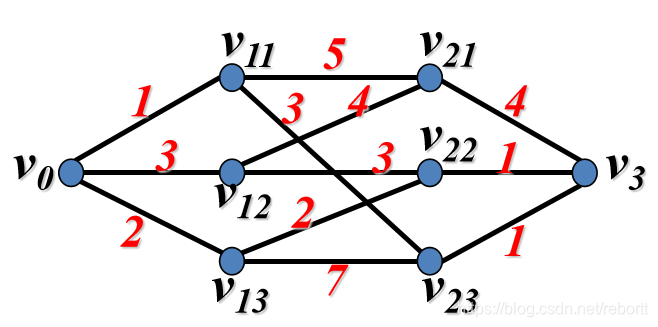
而它的树结构长这样：

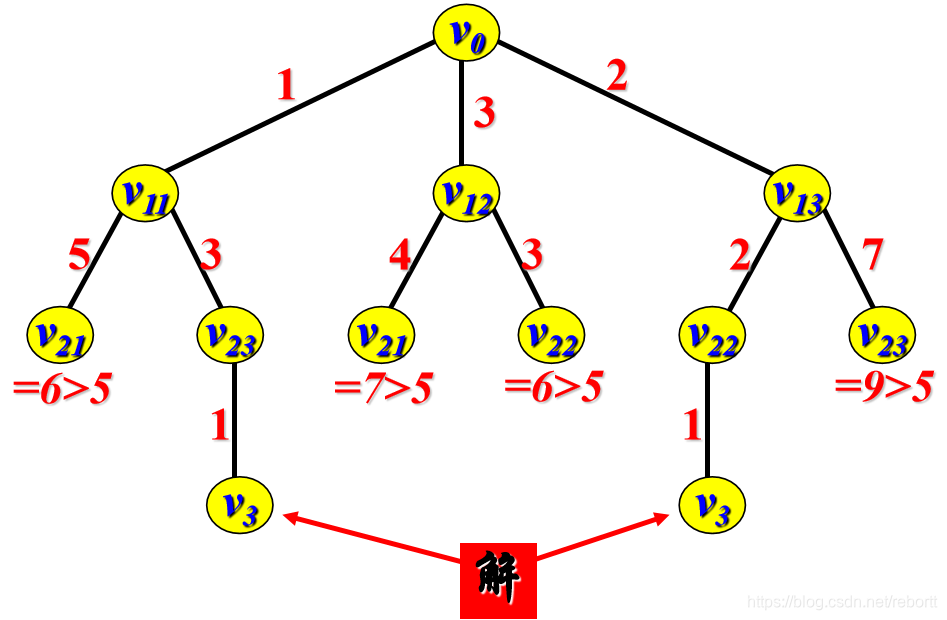
首先我们使用爬山法，先得到了一个长度为5的路径(0->11->23->3)，然后将其作为我们剪枝的判准。
然后我们可以使用best-first算法来寻找最优解了，不过只要当前路径大于5，那么就直接舍弃掉，一定不可能为结果。

问题2，人员安排问题

我们有一个人的集合，和一个任务的集合，同时对应人和任务还有一个代价矩阵C。
要求：

1. 其中人的集合需要从头往后安排，也就是一定要先安排第一个人；
2. 任务是存在拓扑排序的；
3. C[i][j]为第i个人分配第j个任务的代价。

我们需要寻找一个最小的代价。

拓扑排序

先把这个说了，比如我们学习过程中的高数、C语言、数据结构、算法和大物这些吧，
不学高数就不能学大物（因为有微积分），不学C就不能上数据结构，不学数据结构和C就不能学算法。
画一张图：

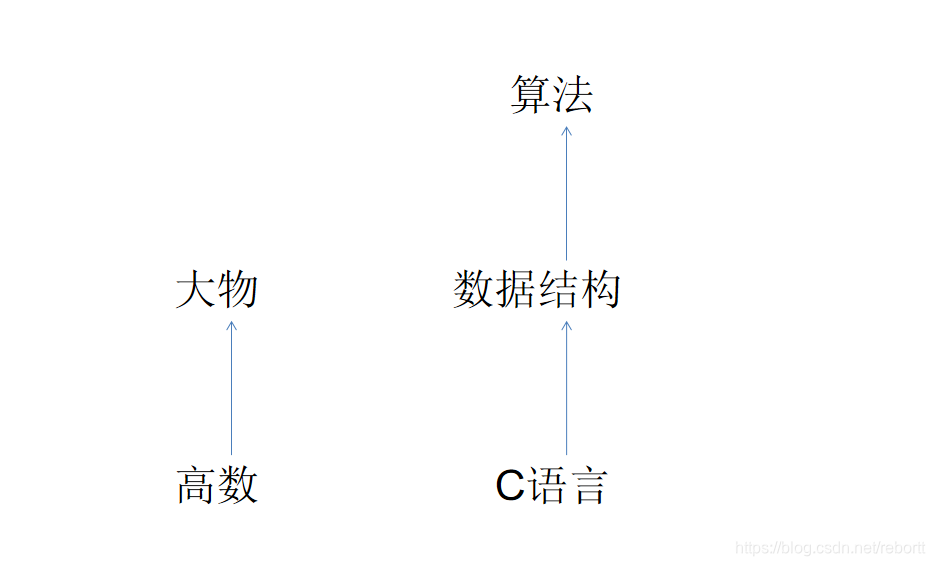
其中高数和C语言谁先上都无所谓，你大一上学期开三门数学课我都不管。
（不会吧不会吧，不会真的有学校大一上三门数学课吧）

这里举例子我们就给出四个活动吧：