Walking on the Safe Side ————动态规划基础题

Walking on the Safe Side

描述：
本题事动态规划中比较常见的一类走格子的题目
在最基础的走格子上，加上了一些不能走的点。
但其本质还是这条式子
dp_map[i][j] = dp_map[i-1][j] + dp_map[i][j-1]

Square City is a very easy place for people to walk around. The two-way streets run North-South or
East-West dividing the city into regular blocks. Most street intersections are safe for pedestrians to
cross. In some of them, however, crossing is not safe and pedestrians are forced to use the available
underground passages. Such intersections are avoided by walkers. The entry to the city park is on the
North-West corner of town, whereas the railway station is on the South-East corner.

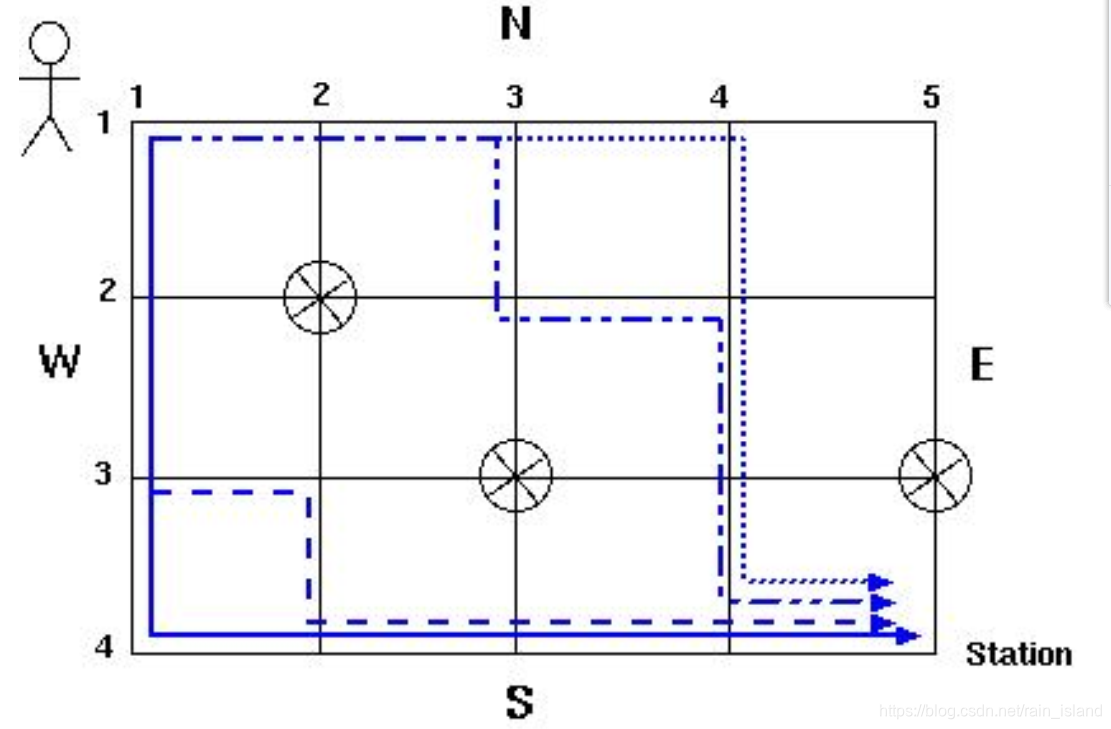
Suppose you want to go from the park to the railway station, and do not want to walk more than
the required number of blocks. You also want to make your way avoiding the underground passages,
that would introduce extra delay. Your task is to determine the number of different paths that you can
follow from the park to the station, satisfying both requirements.
The example in the picture illustrates a city with 4 E-W streets and 5 N-S streets. Three intersections
are marked as unsafe. The path from the park to the station is 3 + 4 = 7 blocks long and there are 4
such paths that avoid the underground passages.
Input
The input begins with a single positive integer on a line by itself indicating the number
of the cases following, each of them as described below. This line is followed by a blank
line, and there is also a blank line between two consecutive inputs.
The first line of the input contains the number of East-West streets W and the number of NorthSouth streets N. Each one of the following W lines starts with the number of an East-West street,
followed by zero or more numbers of the North-South crossings which are unsafe. Streets are numbered
from 1.
Output
For each test case, the output must follow the description below. The outputs of two
consecutive cases will be separated by a blank line.
The number of different minimal paths from the park to the station avoiding underground passages.
Sample Input
1
4 5
1
2 2
3 3 5
4
Sample Output
4

int n,m,M[len][len],dp_map[len][len];
//n表示行数，m为列数
//M二位数字为原图，即可走路线等，dp数组存储走到某个点的路径数

本题最让人难受的输入环节，其他的都只是常规操作（但是我还是wa了若干次）

void Init_map()//M图的初始化
{
    cin >> n >> m;//n行m列
    char s[len];
    int r,num = 0;

    for (int i=0; i<n; i++)
    {
        cin >> r ;//r表示当前读入的行数
        fgets(s,len,stdin);
        unsigned long l = strlen(s);
        for (unsigned long j=0; j<=l; j++)
        {
            if (s[j] >= '0' && s[j] <= '9')
                num = num * 10 + ( s[j] - '0' );
            else
            {
                M[r][num] = -1;
                num = 0;
            }
        }//这里的for循环起到将字符串转换为数字的作用
    }
}

int main()
{
    int c;
    cin >> c;

    while (c--)
    {
        Init_map();
        dp_map[0][1] = 1;

        for (int i=1; i<=n; i++)
        {
            for (int j=1; j<=m; j++)
            {
                if (M[i][j] == -1)
                {
//                    cout << dp_map[i][j] << " ";
                    continue;
                }
                else
                    dp_map[i][j] = dp_map[i-1][j] + dp_map[i][j-1];
//                cout << dp_map[i][j] << " ";
            }
//            cout << endl;
        }

        cout << dp_map[n][m] << endl;
        if (c != 0)
        {
            cout << endl;
        }

//        for (int i=0; i<=n; i++){
//            for (int j=0; j<=m; j++){
//                cout << M[i][j] << " ";
//            }
//            cout << endl;
//        }
//        cout << endl;
//        for (int i=0; i<=n; i++){
//            for (int j=0; j<=m; j++){
//                cout << dp_map[i][j] << " ";
//            }
//            cout << endl;
//        }

        memset(M,0,sizeof(M));
        memset(dp_map,0,sizeof(dp_map));
    }//结束时注意两个图的初始化

    return 0;
}//注释掉的代码是当时为了测试输出的正确性。