数据结构二叉树部分性质

最新推荐文章于 2023-07-05 17:25:40 发布

原创

最新推荐文章于 2023-07-05 17:25:40 发布 · 959 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#b树 #数据结构

本文介绍了二叉树的五个基本性质，包括节点数量与深度的关系、完全二叉树的特性以及二叉查找树的概念。同时，详细讨论了平衡二叉树（AVL树）的平衡调整策略，如LL、RR、LR、RL旋转。此外，还概述了二叉树的三种遍历方法，并解析了在16个元素中查找元素的时间复杂度。最后，提到了2-3树的特性，强调其作为高度平衡查找树的性质。

二叉树性质：

性质1：二叉树的第i层上至多有2i-1（i≥1）个节点
性质2：深度为h的二叉树中至多含有2^h-1个节点
性质3：若在任意一棵二叉树中，有n0个叶子节点，有n2个度为2的节点，则必有n0=n2+1
性质4：具有n个节点的完全二叉树深为log2x+1（其中x表示不大于n的最大整数）
性质5：若对一棵有n个节点的完全二叉树进行顺序编号（1≤i≤n），从上至下从左至右，那么，对于编号为i（i≥1）的节点：

当i=1时，该节点为根，它无双亲节点  
当i>1时，该节点的双亲节点的编号为i/2  
若2i≤n，则有编号为2i的左节点，否则没有左节点
若2i+1≤n，则有编号为2i+1的右节点，否则没有右节点

在这里插入图片描述
完全二叉树：对一颗具有n个结点的二叉树按层编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树（满二叉树一定是完全二叉树，反之则不一定）。
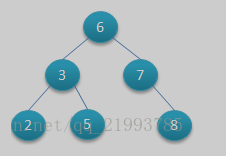
在这里插入图片描述

二叉查找树树：左子树的键值小于根的键值，右子树的键值大于根的键值。
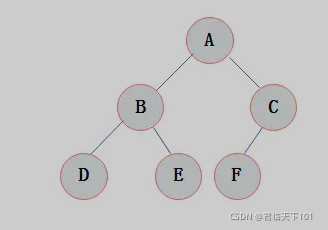
在这里插入图片描述

非空二叉树：至少有一个结点的二叉树叫做非空二叉树。二叉树是每个节点最多有两个子树的树结构。
树

最低0.47元/天解锁文章