位运算
讲解 - 位运算的两种常见操作
位运算只有两种常见的操作:
-
n的二进制中第k位是几:n >> k & 1
假设你有一个数字 n,你想知道它在二进制表示中的第 k 位是 0 还是 1。你可以通过两个步骤来实现:
- 把第
k位移到最后一位:使用右移操作>>把第k位移动到最右边(也就是个位)。 - 查看个位是几:使用按位与操作
&和 1 进行比较,看看个位是 0 还是 1。
具体步骤和例子
步骤 1: 右移操作 n >> k
假设 n = 15,它的二进制表示是 1111。我们想检查第 k 位的值,比如 k = 2。
n的二进制表示是1111。- 我们要检查第
2位,所以进行右移操作n >> 2。当我们进行右移操作n >> k时,实际上是把二进制数的所有位向右移动,高位(左边)补0,低位(右边)被移出。
原始: 1 1 1 1
位数: 3 2 1 0
右移: 1 1 1 1 >> 2 = 0 0 1 1可以看到,第 2 位(从右往左数,第 3 个位置)被移到了最右边。
步骤 2: 按位与操作 & 1
接下来,我们需要确定最右边的位是 0 还是 1。我们用 & 1 来做这个判断。
按位与(&)操作的规则是:
- 0 & 0 = 0
- 0 & 1 = 0
- 1 & 0 = 0
- 1 & 1 = 1
0011
& 0001
------
0001结果是 1,说明原来第 2 位是 1。
-
返回n的最后一位1:lowbit(n) = n & -n
假设你有一个数字 n,你想知道它在二进制表示中最低位的1是几。你可以通过 n & -n 这个操作来实现。
为什么 -n 能帮到我们?
在计算机中,负数是以补码形式存储的。对于一个正数 n,它的负数 -n 的补码可以通过以下步骤得到:
- 先取反(每一位0变1,1变0)
- 再加1
举个例子,如果 n = 6,它的二进制表示是 0110,那么 -n 的计算过程如下:
- 取反:1001
- 加1:1010
所以 -6 在二进制中表示为 1010。
具体步骤和例子
步骤 1: 计算 -n
假设 n = 6,上面已经演示过了,-6的二进制是1010
步骤 2: 按位与操作 n & -n
接下来,我们将 n 和 -n 进行按位与操作:
0110 (n)
& 1010 (-n)
------
0010 (结果)结果是 0010,也就是十进制的 2。
总结为公式就是:
x&−x=x&(∼x+1)一个数 x 与上他本身的相反数,等于x与上本身取反后加一。
做题模板
运用位运算的两种常见操作,就可以得到这个数的二进制表示。
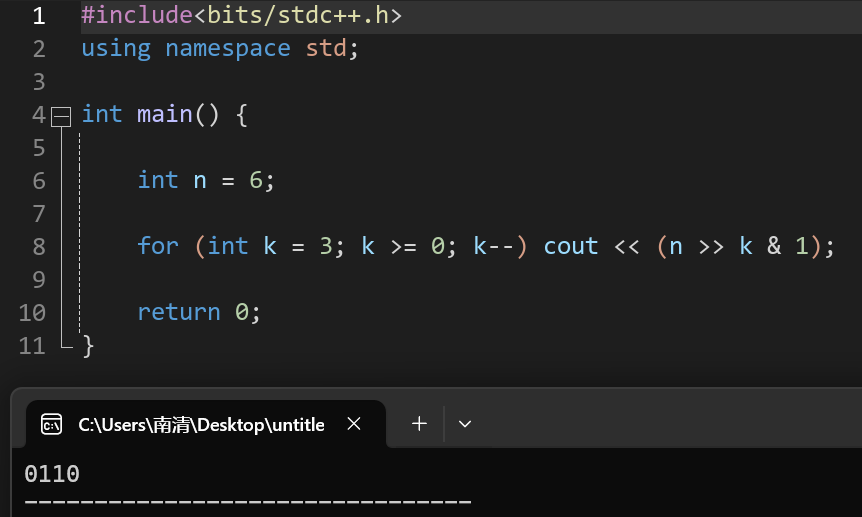
模板题
#include<bits/stdc++.h>
using namespace std;
// 3.1 定义lowbit函数
// 提取 x 的二进制中最右边的 1 所代表的数值
int lowbit(int x) {
// 利用补码性质
// -x 是 ~x + 1,x & -x 得到最低位的1
return x & -x;
}
int main() {
int n;
cin >> n;
while(n--){
int x;
cin >> x;
// 1.记录二进制中1的个数,初始为0
int res = 0;
// 2.循环:不断去掉x最右边的1,直到x变为0
while(x){
// 3.使用lowbit函数:每次减去x的最低位的1
x -= lowbit(x);
// 4.每去掉一个1,计数器加1
res++;
}
cout << res << ' ';
}
return 0;
}
双指针算法
讲解
双指针算法的用途有非常多,KMP也算是双指针算法。双指针的核心思想就是优化。朴素的双重循环算法具有 O(n^2)的时间复杂度,而通过巧妙地使用双指针,可以将时间复杂度优化到 O(n)。
// 朴素算法 O(n^2)
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
// 检查条件
}
}
// 双指针算法 O(n)
for (int i = 0, j = 0; i < n; i++) {
while (j < i && check(i, j)) j++;
// 每道题目的具体逻辑
}第一类:指向两个序列
这类双指针算法通常用于处理两个独立的序列,比如归并排序中的合并过程。
示例:归并排序
在归并排序中,我们需要将两个有序序列合并成一个有序序列。此时可以使用两个指针分别指向两个序列的起始位置,逐个比较并合并。
第二类:指向一个序列(区间)
这类双指针算法通常用于在一个序列中寻找满足特定条件的子区间。快速排序中的分区操作就是一个典型例子。
示例:快速排序
在快速排序的分区过程中,我们需要找到一个基准值,并将小于基准值的元素放在左边,大于基准值的元素放在右边。此时可以使用两个指针分别从两端向中间移动,交换不符合条件的元素。
两种都可以见博客:算法详细讲解- 快速排序与归并排序-优快云博客
统一模板
所有的双指针算法都可以归类为一个统一的模板,如下所示:
for (int i = 0, j = 0; i < n; i++) {
while (j < i && check(i, j)) j++;
// 每道题目的具体逻辑
}- 外层循环:
for (int i = 0, j = 0; i < n; i++),控制一个指针i从左到右遍历整个序列。 - 内层循环:
while (j < i && check(i, j)) j++;,控制另一个指针j根据特定条件进行移动。
举一个例子:
#include<bits/stdc++.h>
using namespace std;
// 例子:输入abc def ghi,每个单词输出并空格隔开
char str[1000];
int main() {
gets(str);
int n = strlen(str);
// 移动i指针
for (int i = 0; i < n; i++) {
int j = i;
// 移动j指针,遇到空格就停下
while(j < n && str[j] != ' ') j++;
// 这道题的具体逻辑
for (int k = i; k < j; k++) cout << str[k];
cout << endl;
i = j;
}
return 0;
}做题模板
1. 朴素做法(双重循环)
- 时间复杂度为 O(n2)O(n2)。
- 使用两个嵌套循环遍历数组中的所有子数组,并检查每个子数组是否满足条件。
- 对于每个右端点
i,从左端点j = 0开始逐个检查到j = i。
// 朴素做法:O(n^2)
for (int i = 0; i < n; i++) {
for (int j = 0; j <= i; j++) {
if (check(j, i)) { // 检查子数组 [j, i] 是否满足条件
res = max(res, i - j + 1); // 更新结果
}
}
}2. 双指针算法
- 时间复杂度为 O(n)O(n)。
- 使用两个指针
i和j遍历数组,通过移动指针来动态调整子数组范围。 - 当子数组
[j, i]不满足条件时,移动左指针j,直到子数组满足条件。
// 双指针算法:O(n)
for (int i = 0, j = 0; i < n; i++) {
while (j <= i && check(j, i)) j++; // 移动左指针 j,直到不满足条件
res = max(res, i - j + 1); // 更新结果
}- 优化关键:在朴素做法中,每次右端点
i固定时,需要从左端点j = 0开始逐个检查到j = i。而在双指针算法中,左指针j只需要根据条件进行相应的调整,避免了重复计算。 - 动态调整:当右指针
i向右移动时,左指针j可以直接跳过已经检查过的部分,从而将时间复杂度从 O(n2)O(n2) 优化到 O(n)O(n)。
模板题
给定一个长度为 n 的整数序列,请找出最长的不包含重复的数的连续区间,输出它的长度。
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
int n; // 存储序列长度
int a[N]; // 存储输入的整数序列
int s[N]; // 频次数组:s[x] 表示数字 x 在当前区间 [j, i] 中出现的次数
int main() {
// 读入序列长度 n
cin >> n;
// 读入 n 个整数到数组 a 中
for (int i = 0; i < n; i++) {
cin >> a[i];
}
// 用于记录最长不重复区间的长度,初始为 0
int res = 0;
// 双指针算法主循环
// i 是右指针,j 是左指针,共同维护一个不包含重复数字的滑动窗口 [j, i]
for (int i = 0, j = 0; i < n; i++) {
// 第一步:将右端点 a[i] 加入当前区间
s[a[i]]++; // a[i] 的出现次数加 1
// 第二步:如果 a[i] 重复了(出现次数 > 1),就要移动左指针 j,缩小窗口
// 直到 a[i] 的频次降为 1,即区间内不再有重复
while (s[a[i]] > 1) {
s[a[j]]--; // 把左端点 a[j] 移出区间,它的频次减 1
j++; // 左指针右移
}
// 第三步:此时区间 [j, i] 是合法的(无重复),更新最大长度
res = max(res, i - j + 1); // 当前区间长度为 i - j + 1
}
cout << res << endl;
return 0;
}给定两个升序排序的有序数组 A 和 B,以及一个目标值 x。请你求出满足 A[i]+B[j]=x 的数对 (i,j)。
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int n, m, x, a[N], b[N];
int main() {
scanf("%d%d%d", &n, &m, &x);
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
}
for (int i = 0; i < m; i++) {
scanf("%d", &b[i]);
}
// 双指针法求两数之和(适用于两个有序数组)
// 思路:
// - 指针 i 从数组 A 的起始位置(0)开始,向右移动(从小到大)
// - 指针 j 从数组 B 的末尾位置(m-1)开始,向左移动(从大到小)
// - 利用两个数组有序的性质,动态调整 j 的位置,使得 a[i] + b[j] 接近 x
// 初始化:i 从 0 开始,j 从 B 的最后一个元素开始
for (int i = 0, j = m - 1; i < n; i++) {
// 当前 a[i] 固定时,如果 a[i] + b[j] 太大,说明 b[j] 太大
// 因为 b 是升序的,所以 j 要左移(j--),尝试更小的 b[j]
// 循环条件:j >= 0 保证不越界,且 a[i] + b[j] > x 时需要减小和
while (j >= 0 && a[i] + b[j] > x) {
j--;
}
// 退出 while 后,有两种可能:
// 1. j < 0:说明 B 中所有元素都太小,无法与 a[i] 配对达到 x(但题目保证有唯一解,所以不会发生)
// 2. a[i] + b[j] <= x,此时我们检查是否正好等于 x
if (j >= 0 && a[i] + b[j] == x) { // 注意:j 可能已变为 -1,需判断
// 找到唯一解:输出下标 i 和 j
printf("%d %d\n", i, j);
break; // 题目保证有唯一解,找到后即可退出
}
// 如果 a[i] + b[j] < x,说明 a[i] 太小,进入下一轮循环,i++,尝试更大的 a[i]
// 此时 j 保持不变或已经调整过,继续用于下一个 i
}
return 0;
}练习题
这道题与上面唯一不同的是序列是未排序,而且是需要去重的,题解如下:
class Solution {
public:
int longestConsecutive(vector<int>& nums) {
if (nums.empty()) return 0;
sort(nums.begin(), nums.end());
nums.erase(unique(nums.begin(), nums.end()), nums.end());
int res = 1, len = 1;
for (int i = 1; i < nums.size(); i++) {
if (nums[i] == nums[i-1] + 1) {
len++;
} else {
len = 1;
}
res = max(res, len);
}
return res;
}
};在这里,去掉重复元素的统一固定做法是:
nums.erase(unique(nums.begin(), nums.end()), nums.end()); 位运算与双指针算法详解
位运算与双指针算法详解




















 168万+
168万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








