损失函数
神经网络里的标准和人脑标准相比较 相差多少的定量表达。
最小二乘法
首先要搞明白两个概率模型是怎么比较的。有三种思路,最小二乘法、极大似然估计,交叉熵

极大似然估计
似然值是真实的情况已经发生,我们假设它有很多模型,在这个概率模型下,发生这种情况的可能性就叫似然值。
挑出似然值最大的,那可能性也就越高,此时的概率模型应该是与标准模型最接近的。
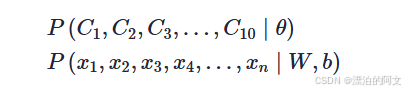
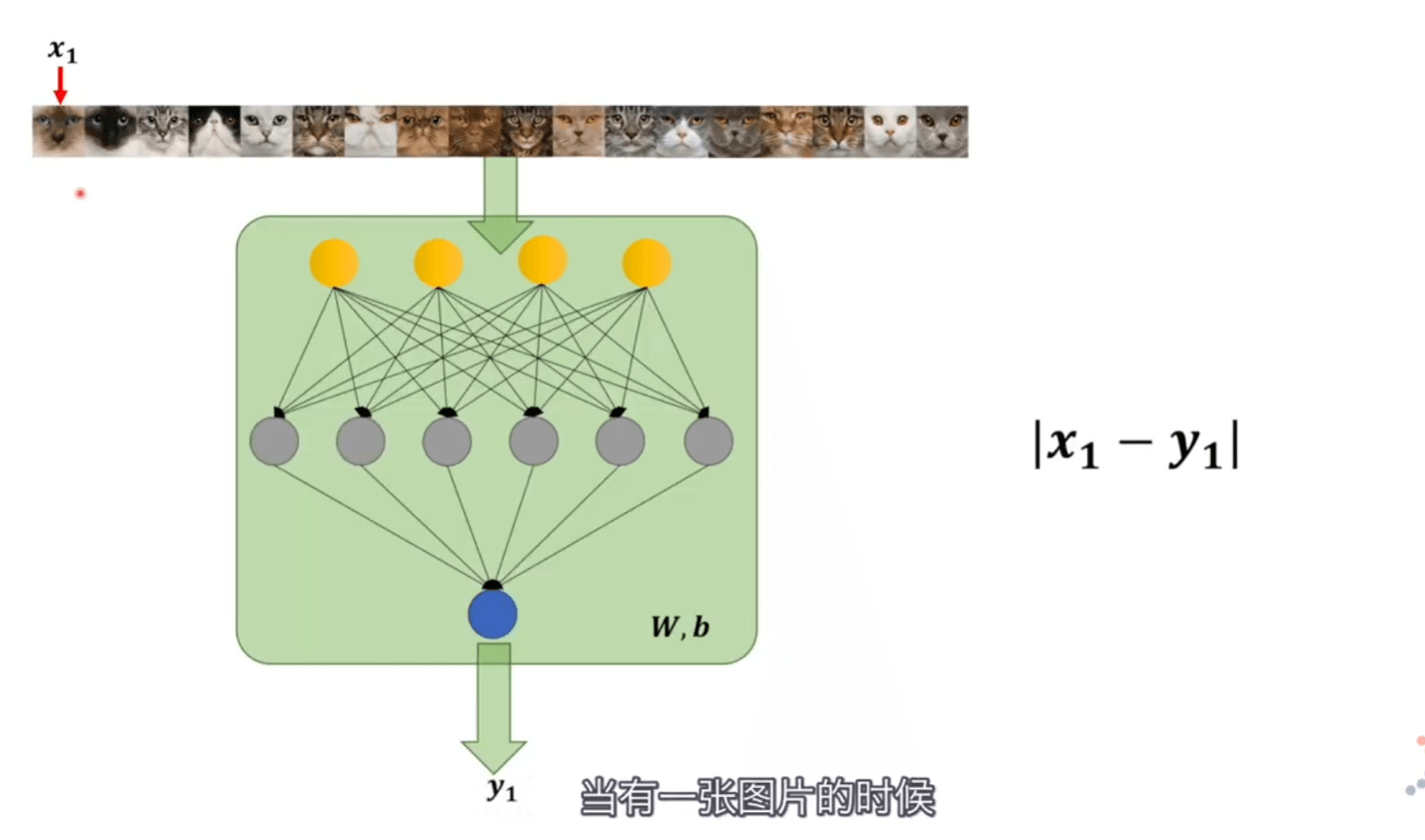
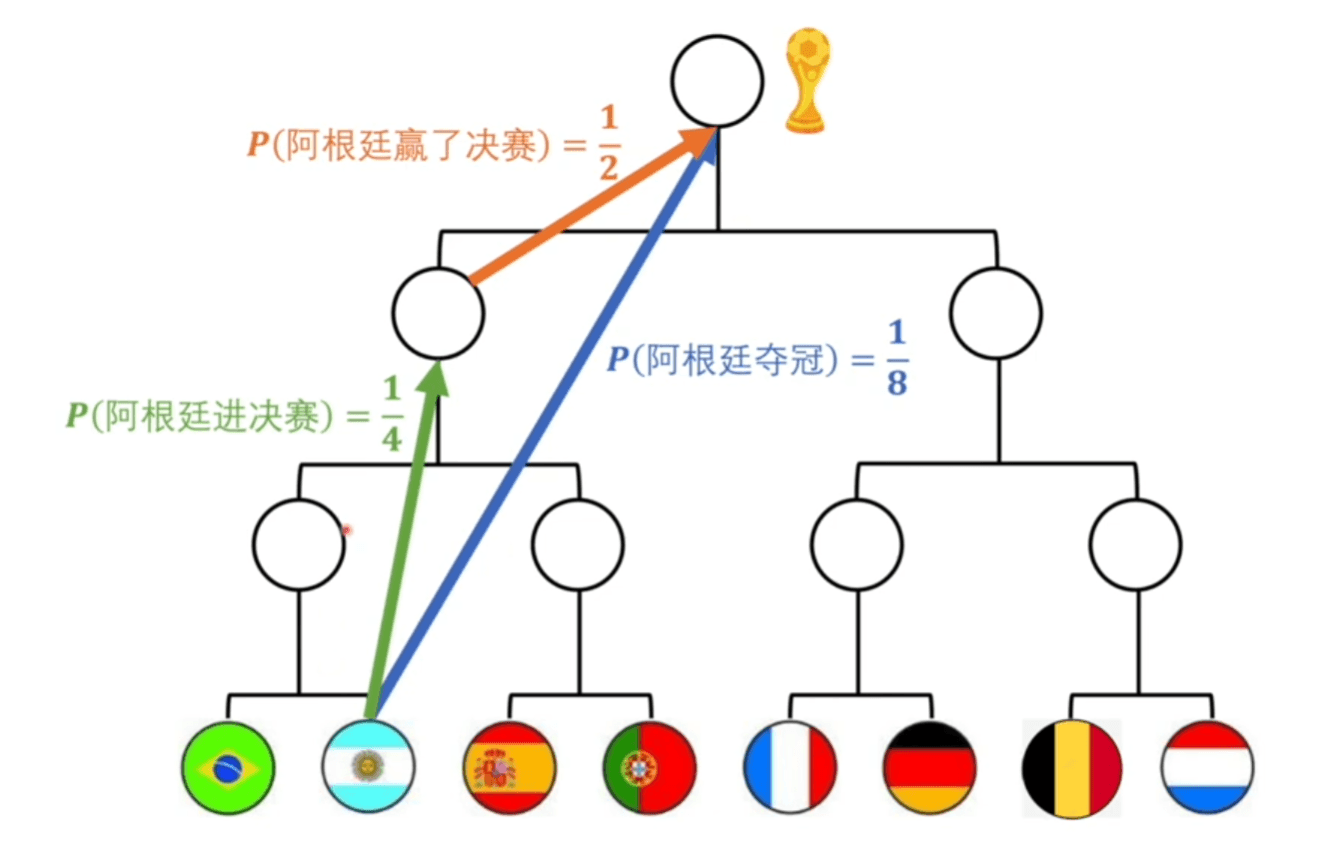
θθ 是抛硬币的概率模型,W,bW,b 是神经网络的概率模型。前者结果是硬币是正还是反,后者结果是图片到底是不是猫。
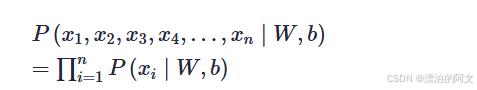
在神经网络是这样的参数下,输入的照片如果是猫概率是多少、如果不是猫概率是多少,所有图片判断后,相乘得到的值就是似然值。取到极大似然值就是最接近的值。
但在训练的时候 W、b 无论输入什么样的照片都是固定的值,如果我们都用猫的照片来确定的话标签都是11,那就没有办法进行训练,理论可行却没有操作性。但是我们还可以利用条件,训练神经网络的时候既可以得到 xi也可以得到 yi的输出结果依赖 W,b 。每次输入照片不一样,yi的结果也就不一样。
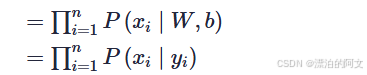
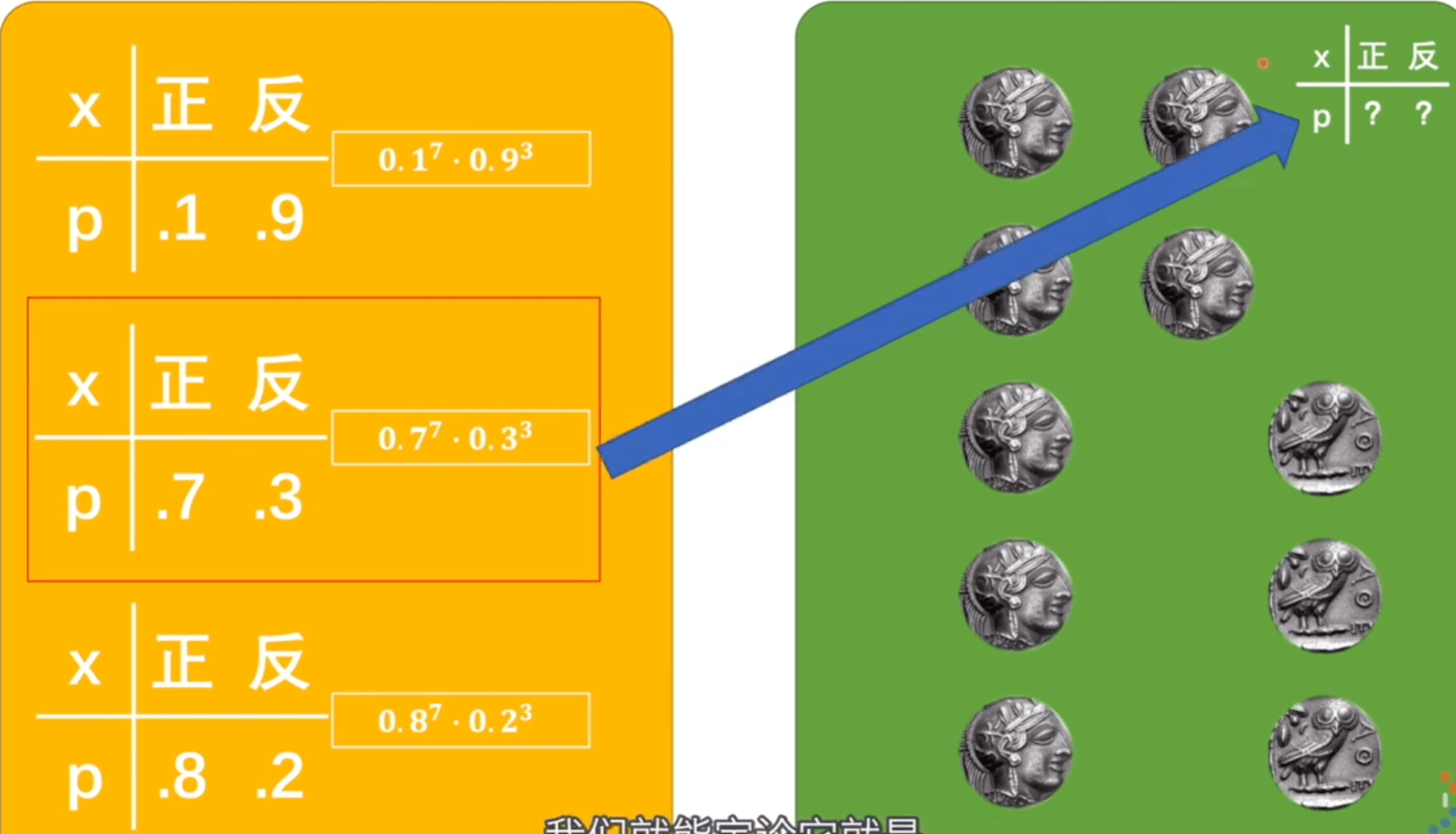
xi的取值是 0,1 ,符合二项伯努利分布,概率分布表达式为
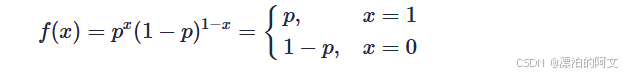
x=1就是图片为猫的概率。而 p就是 yi(神经网络认定是猫的概率),将其带入替换 P(xi∣yi)
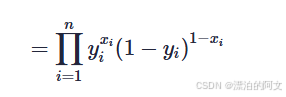
我们更喜欢连加,在前面加 log ,并化简
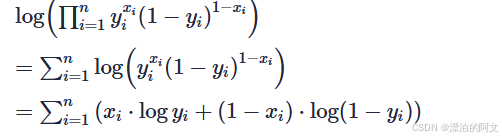
所以,求极大似然值,就是求如下公式
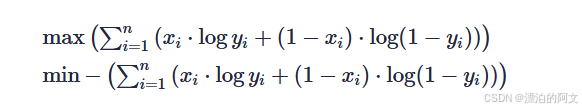
复习一下对数
交叉熵
要想直接比较两个模型,前提是两个模型类型是同一种,否则就不能公度。概率模型如果想要被统一衡量,我们需要引入熵(一个系统里的混乱程度)。
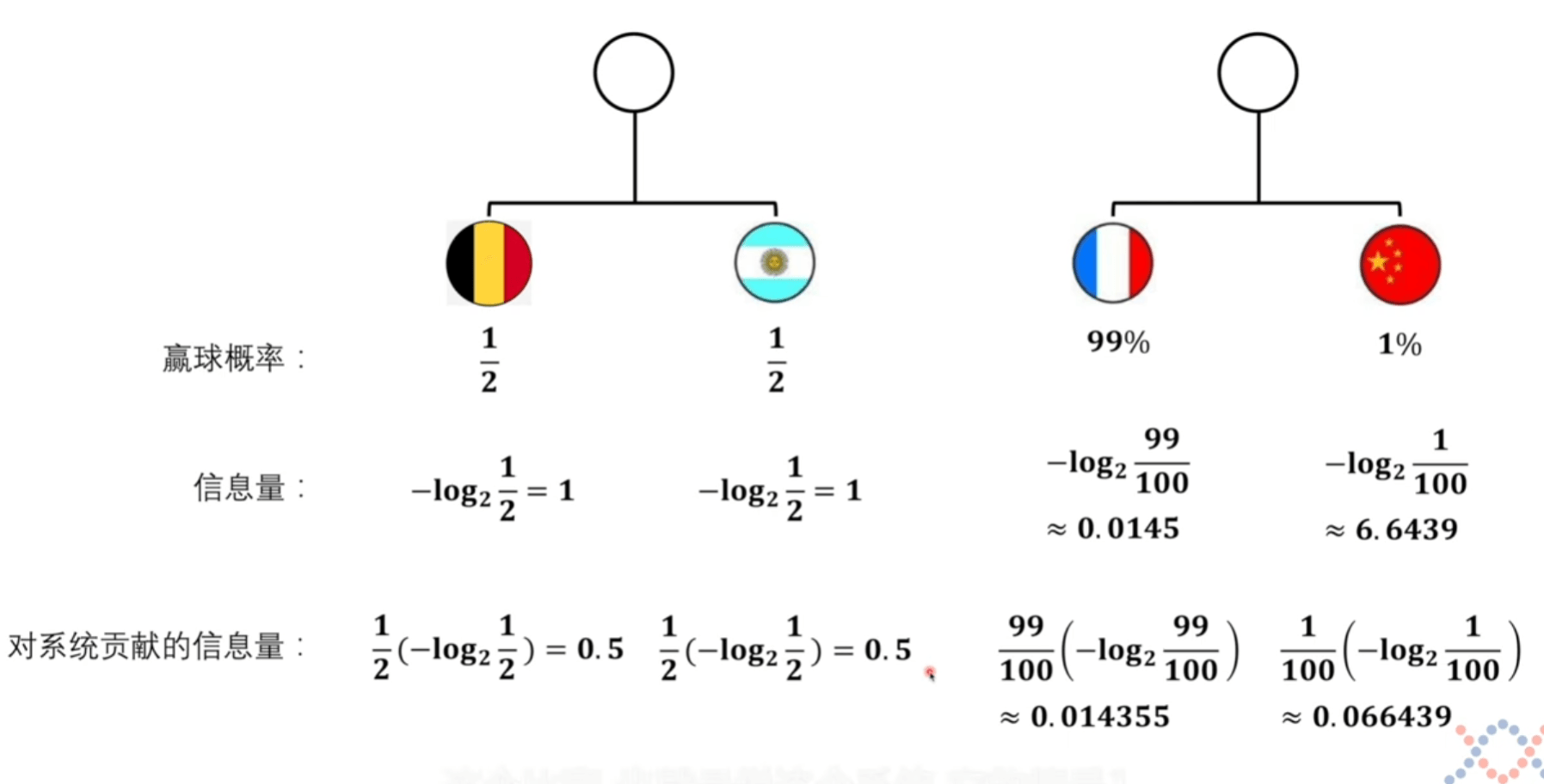
信息量
我们想获取信息量的函数,就要进行定义。并找寻能让体系自洽的公式。

将上面的第四条公式带入第三条得到如下第二条。为了使信息量定义能让体系自洽,我们给定定义 log,这样符合相乘变相加的形式。
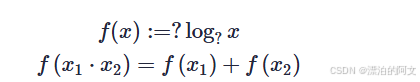
为了符合我们最直观的感觉,因为概率越小,信息量越大。而 log 函数单调递增,我们转换方向。
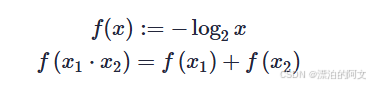

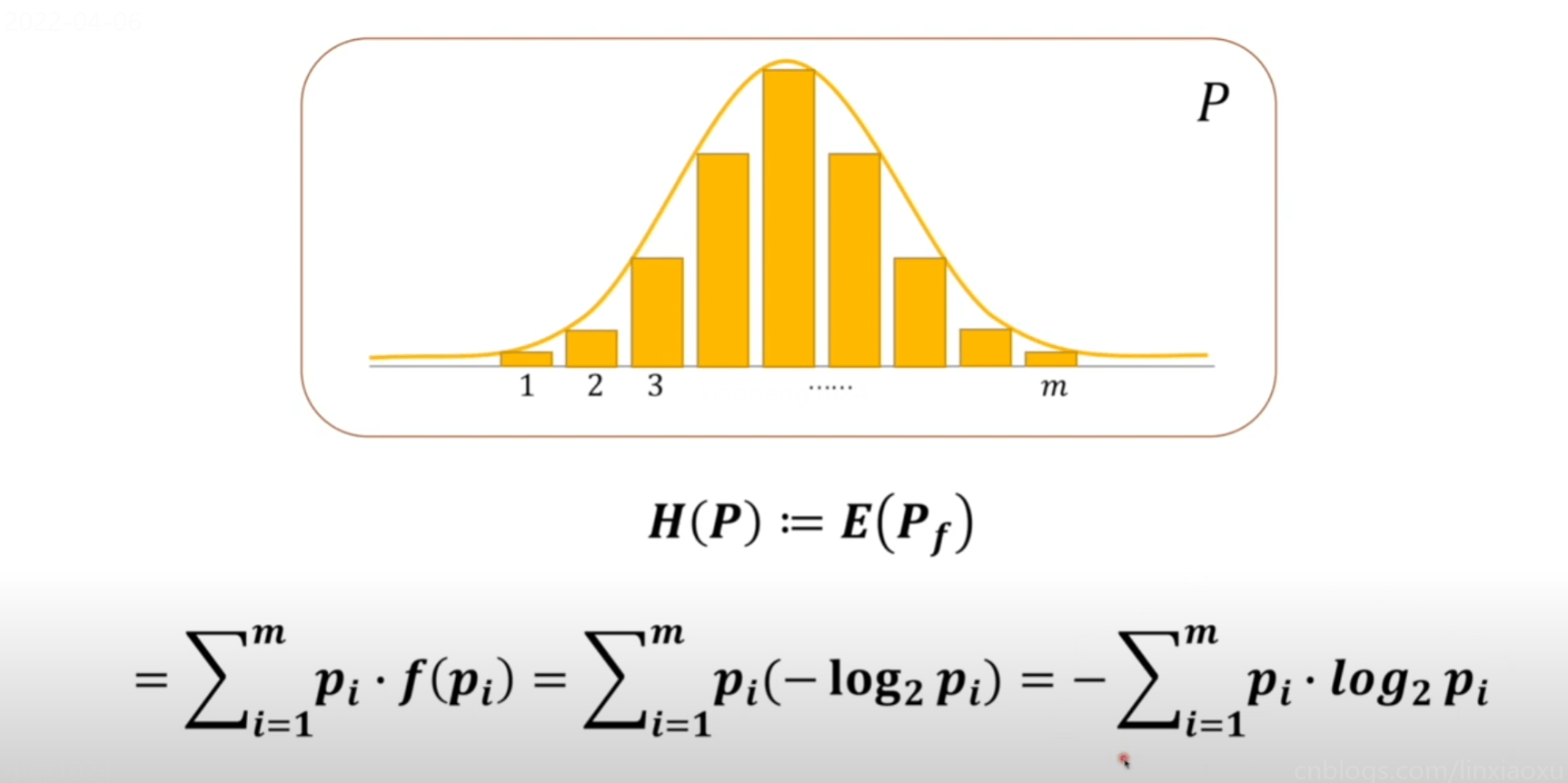
系统熵的定义
将上方对系统贡献的信息量可以看成是期望的计算。
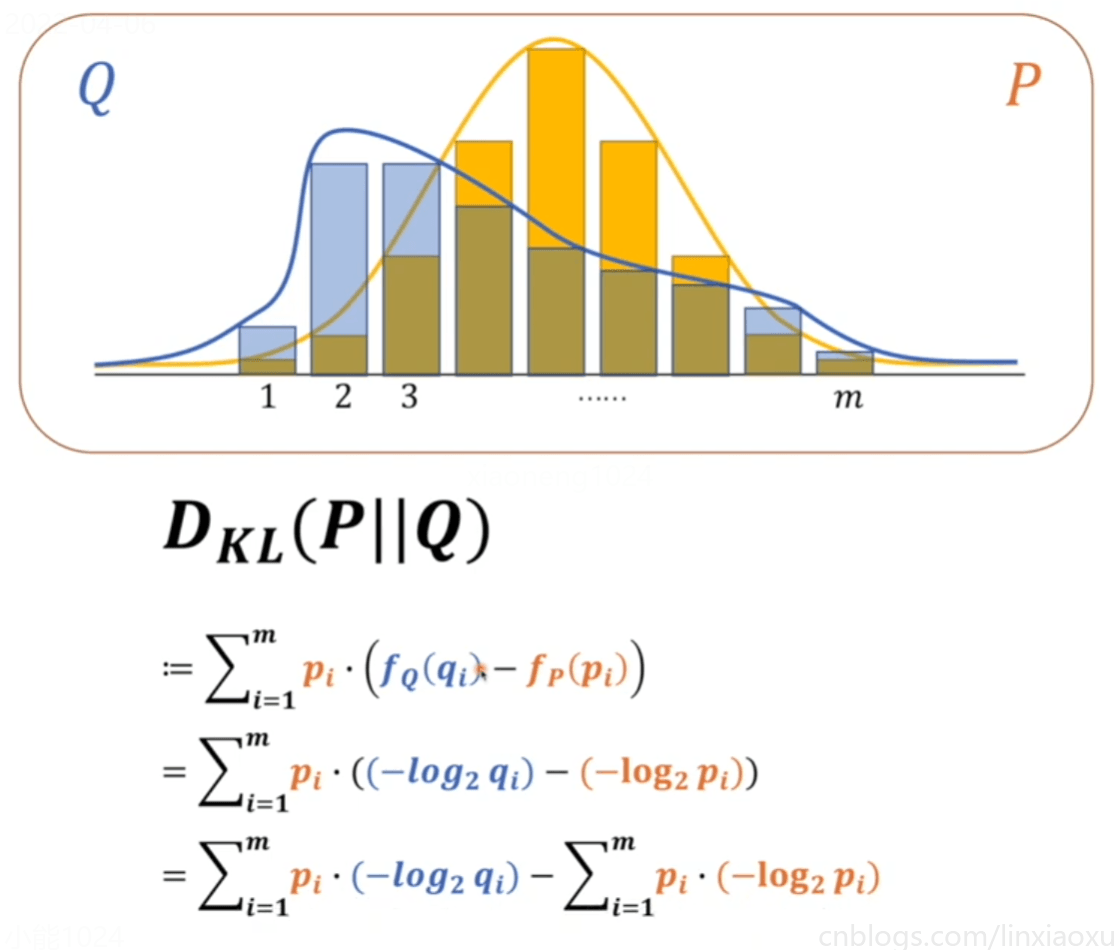
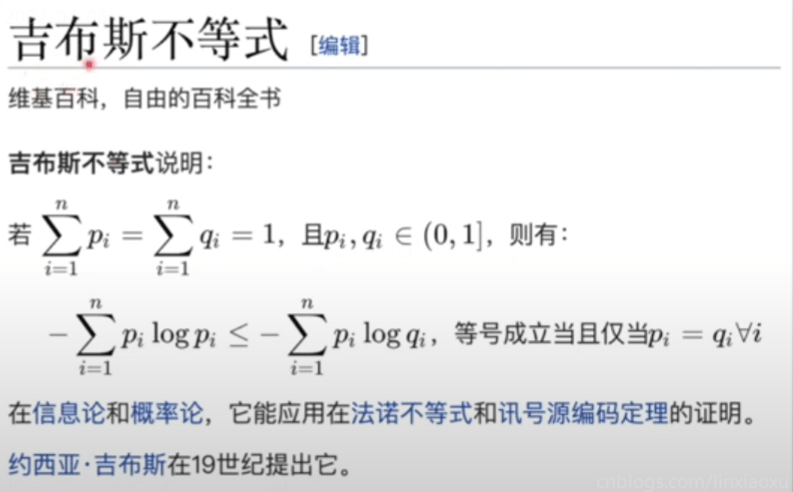
KL散度

原文地址: https://www.cnblogs.com/linxiaoxu/p/16111397.html






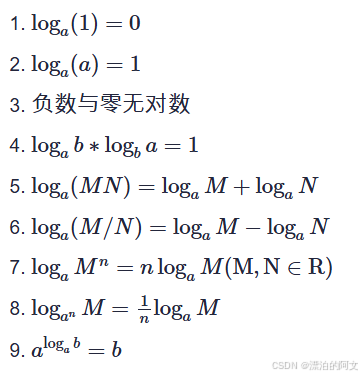

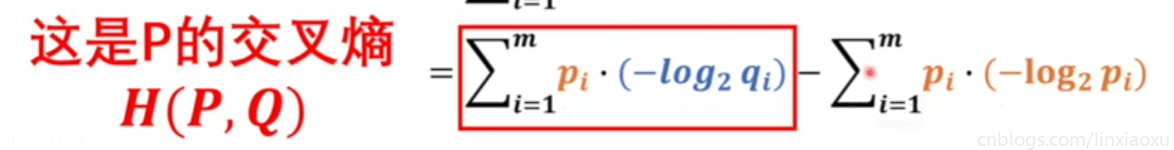
















 1155
1155










