提示技术系列（三）——链式思考（CoT）

原创已于 2025-07-05 21:04:55 修改 · 1.2k 阅读

29 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #prompt #python

于 2025-06-28 18:37:29 首次发布

提示技术专栏收录该内容

14 篇文章

订阅专栏

什么是提示技术？

提示技术是实现提示工程目标的具体技术手段，是提示工程中的“工具库”。

什么又是提示工程？

提示工程是指通过设计、优化和迭代输入到大语言模型（LLM）的提示（Prompt），系统性提升模型输出质量（如相关性、准确性、可控性）的实践领域。它是一个覆盖全流程的方法论，包括：

明确目标任务（如生成教学内容、问答、翻译）；
设计提示结构（如指令、上下文、示例）；
选择模型与参数（如温度、top_p）；
- 验证与迭代（根据输出调整提示）。

其核心是“通过工程化方法控制大语言模型（LLM）的行为”。

概念

思维链提示（Chain of Thought Prompt）是一种通过在问题和答案之间插入中间推理步骤，引导模型分步骤推理的技术。

这种提示方式让模型不仅输出最终答案，还展示其推理路径，类似于人类解决问题的逐步思考过程。

链式思考（CoT）技术的核心在于分解复杂问题为多个可管理的子问题，从而提升推理的准确性、可解释性和透明度。

链式思考（CoT）常见类型：

零样本（CoT）提示；
链式思考提示（含少样本CoT）；
自动思维链（Auto-CoT）

零样本（CoT）提示，是一种特例，它只是在输入的问题中加上一行“让我们逐步思考”。

自动思维链提示（Auto-CoT），是一种自动构建思维链提示的方法。其核心思想是利用 LLM 自身的推理能力来生成示例，从而避免人工设计的繁琐过程，并提高推理效率。

概念图解

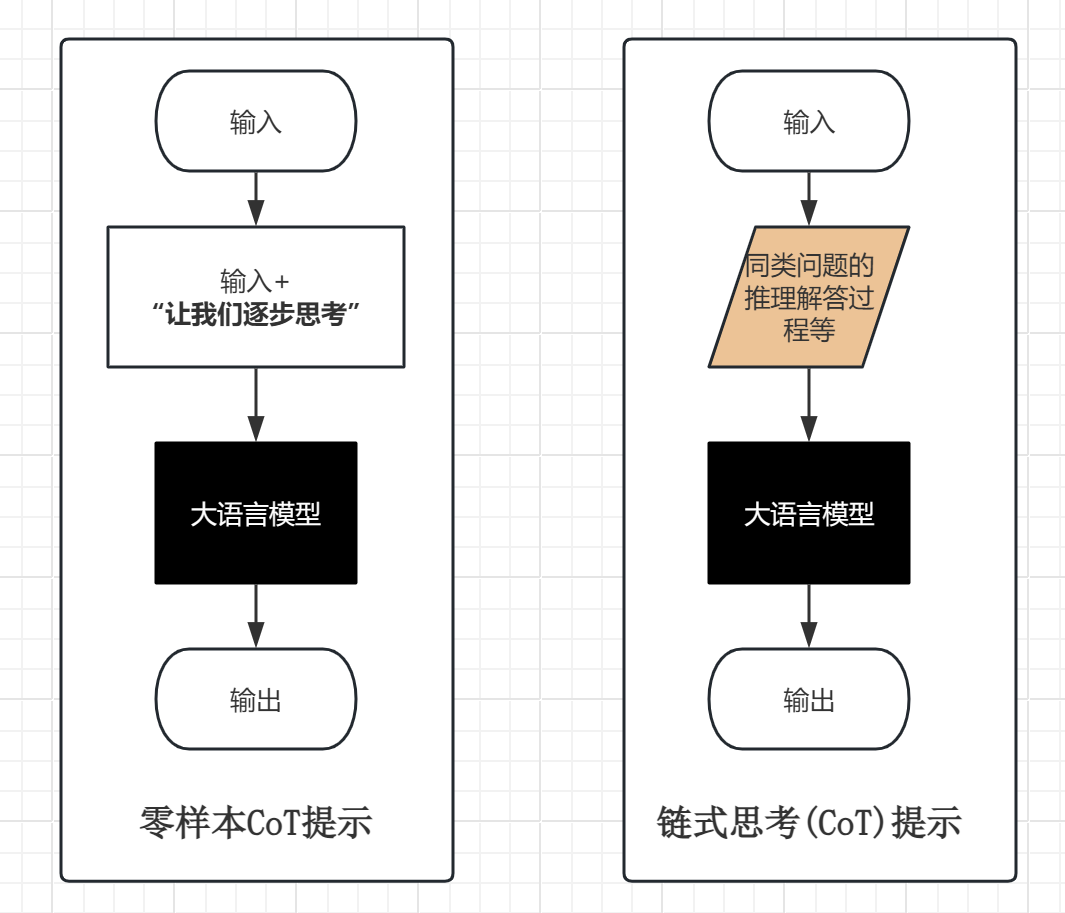
应用场景

在理解应用场景前，先明确 CoT 的核心价值：

提升复杂问题解决能力：通过分步推理，大语言模型能更系统地处理多条件、多约束的问题。
增强答案可解释性：输出包含“思考过程”，便于验证逻辑正确性（如数学题的步骤验证）。
降低错误率：通过显式展示推理步骤，减少大语言模型因“跳跃性思维”导致的错误（如漏算、误判等）。

数学题解答（尤其是复杂计算或多步推理）；
逻辑推理题（如谜题、推理题分析）；
代码调试；
……

案例实操

数学题解答（尤其是复杂计算或多步推理）

prompt：

请逐步证明“平行四边形的对角线互相平分”，要求：
1. 先写出平行四边形的定义（两组对边分别平行）；
2. 标记对角线AC和BD的交点为O；
3. 利用三角形全等（SAS）证明AO=OC，BO=OD。

运行结果如下：

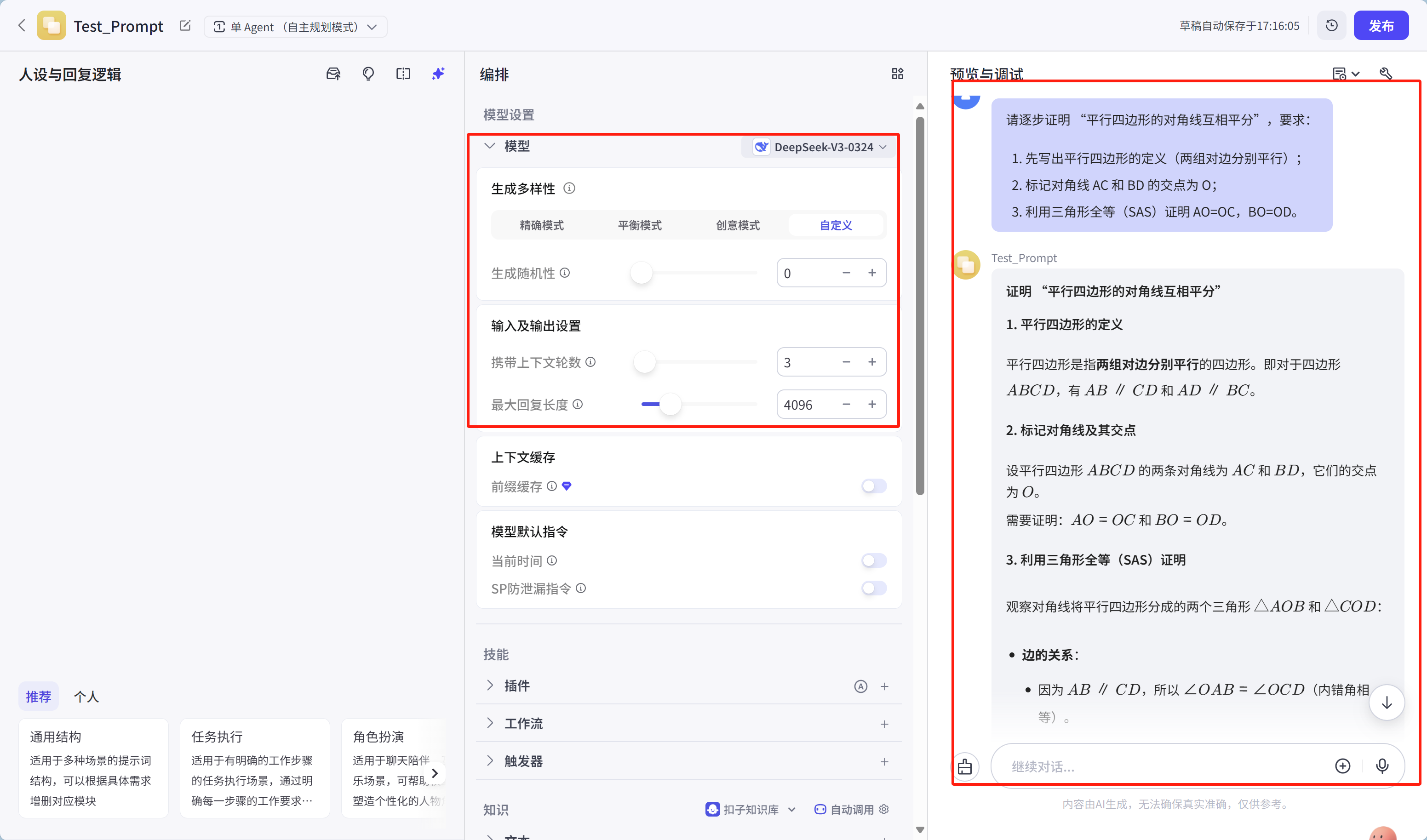
具体结果内容：

证明“平行四边形的对角线互相平分”

1. 平行四边形的定义

平行四边形是指两组对边分别平行的四边形。即对于四边形 ( ABCD )，有 ( AB \parallel CD ) 和 ( AD \parallel BC )。

2. 标记对角线及其交点

设平行四边形 ( ABCD ) 的两条对角线为 ( AC ) 和 ( BD )，它们的交点为 ( O )。
需要证明：( AO = OC ) 和 ( BO = OD )。

3. 利用三角形全等（SAS）证明

观察对角线将平行四边形分成的两个三角形 ( \triangle AOB ) 和 ( \triangle COD )：

边的关系：

因为 ( AB \parallel CD )，所以 ( \angle OAB = \angle OCD )（内错角相等）。
因为 ( AD \parallel BC )，所以 ( \angle OBA = \angle ODC )（内错角相等）。
因为平行四边形的对边相等，所以 ( AB = CD )。

全等条件：

( \angle OAB = \angle OCD )（对应角相等），
( AB = CD )（对应边相等），
( \angle OBA = \angle ODC )（对应角相等）。
因此，( \triangle AOB \cong \triangle COD )（ASA 全等）。

对应边相等：

由全等可知，( AO = OC ) 和 ( BO = OD )。

结论

平行四边形的对角线 ( AC ) 和 ( BD ) 在交点 ( O ) 处互相平分，即 ( AO = OC )，( BO = OD )。

逻辑推理题（如谜题、推理题分析）

prompt：

三个嫌疑人A、B、C中，只有一人偷了钻石，只有一人说假话。已知：
◦ A说：“不是我偷的。”
◦ B说：“是C偷的。”
◦ C说：“是A偷的。”
谁是小偷？
请通过逻辑推理找出小偷，步骤如下：
1. 假设A是小偷，验证三人陈述是否矛盾；
2. 假设B是小偷，验证三人陈述是否矛盾；
3. 假设C是小偷，验证三人陈述是否矛盾；
4. 总结唯一无矛盾的情况。

运行结果如下：

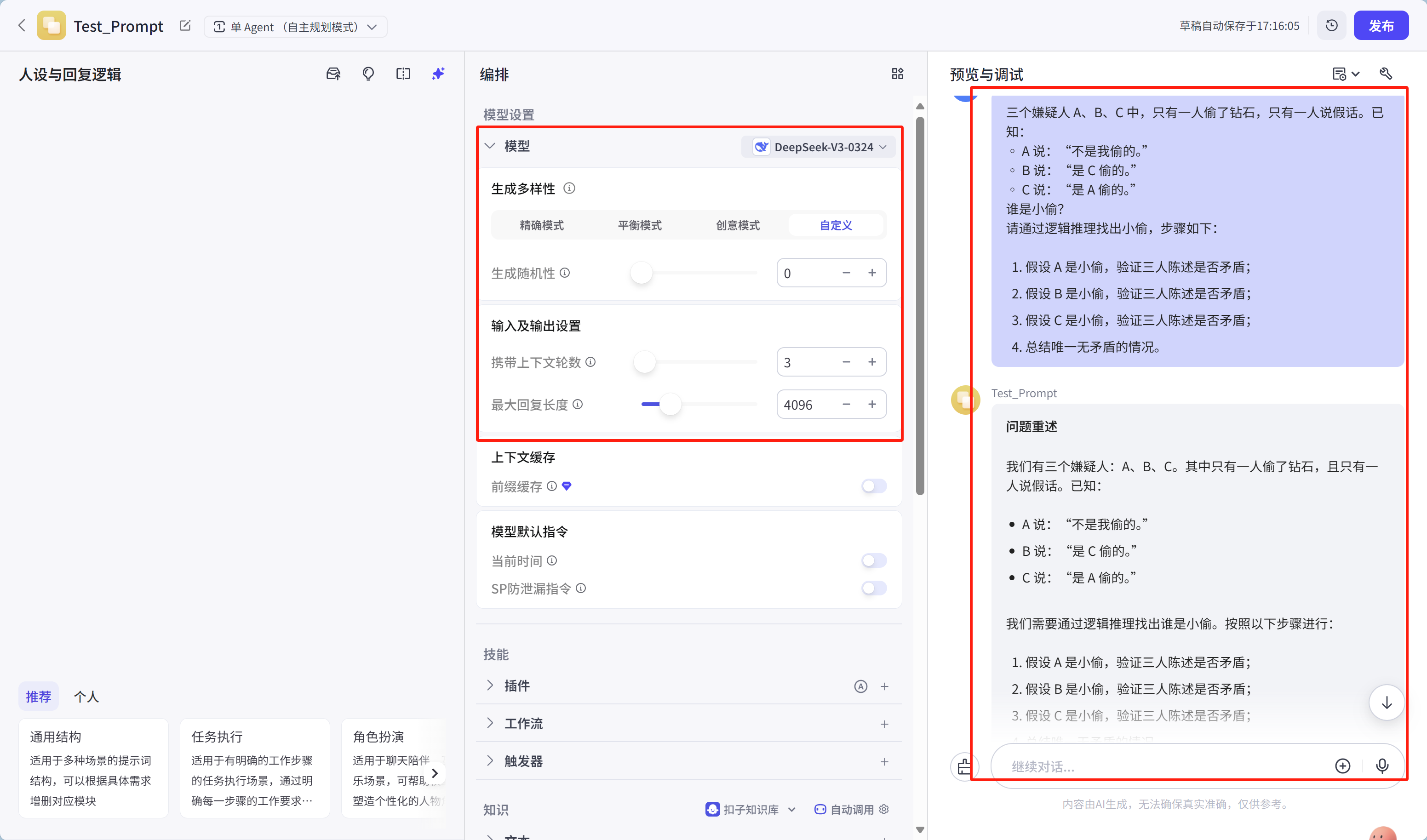
具体结果内容：

问题重述

我们有三个嫌疑人：A、B、C。其中只有一人偷了钻石，且只有一人说假话。已知：

A说：“不是我偷的。”
B说：“是C偷的。”
C说：“是A偷的。”

我们需要通过逻辑推理找出谁是小偷。按照以下步骤进行：

假设A是小偷，验证三人陈述是否矛盾；
假设B是小偷，验证三人陈述是否矛盾；
假设C是小偷，验证三人陈述是否矛盾；
总结唯一无矛盾的情况。

解题步骤

假设1：A是小偷

A是小偷：

此时，A和B都在说假话，但题目规定只有一人说假话。因此，此假设与条件矛盾，A不可能是小偷。

A说：“不是我偷的。” → 这是假话，因为实际是A偷的。
B说：“是C偷的。” → 这是假话，因为实际是A偷的。
C说：“是A偷的。” → 这是真话。

假设2：B是小偷

B是小偷：

此时，B和C都在说假话，但题目规定只有一人说假话。因此，此假设与条件矛盾，B不可能是小偷。

A说：“不是我偷的。” → 这是真话，因为实际是B偷的。
B说：“是C偷的。” → 这是假话，因为实际是B偷的。
C说：“是A偷的。” → 这是假话，因为实际是B偷的。

假设3：C是小偷

C是小偷：

此时，只有C在说假话，A和B都说真话，完全符合“只有一人说假话”的条件。因此，C是小偷。

A说：“不是我偷的。” → 这是真话，因为实际是C偷的。
B说：“是C偷的。” → 这是真话，因为实际是C偷的。
C说：“是A偷的。” → 这是假话，因为实际是C偷的。

验证

让我们再验证一下：

小偷是C：

只有C说假话，其他两人说真话，且只有C是小偷，完全符合题目所有条件。

A说：“不是我偷的。” → 真。
B说：“是C偷的。” → 真。
C说：“是A偷的。” → 假。

排除其他可能性

为了确保我们的答案唯一，我们再看看其他两种假设：

A是小偷：

A假，B假，C真 → 两人假话，矛盾。

B是小偷：

A真，B假，C假 → 两人假话，矛盾。

C是小偷：

A真，B真，C假 → 一人假话，符合。

因此，只有C是小偷的情况满足所有条件。

结论

通过以上逻辑推理和验证，可以确定：

C是小偷。

代码调试（如解决程序错误、优化逻辑）

prompt：

请逐步调试以下代码，找出错误并修正：
输入列表：[1, 2, 2, 3, 1]
目标：输出去重后的列表[1, 2, 3]
原始代码：
def deduplicate(lst):
new_lst = []
for i in lst:
if i not in new_lst:
new_lst.append(i)
return new_lst
调用结果：[1, 2, 3]（正确），但用户反馈“运行时报错：NameError: name 'new_lst' is not defined”。
步骤：
1. 检查代码语法错误；
2. 分析函数定义与调用是否匹配；
3. 验证变量作用域。

运行结果如下：

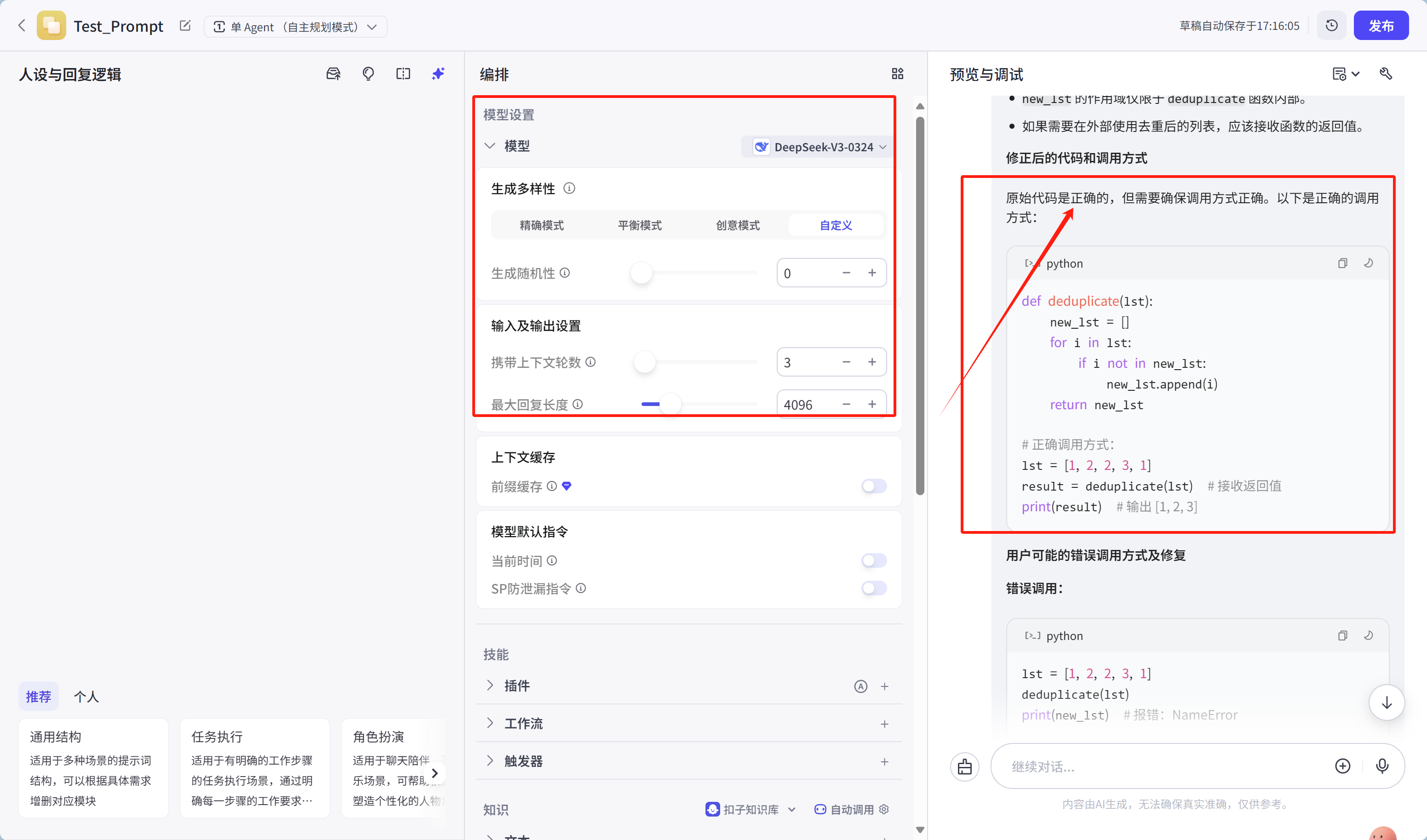
给出的代码案例如下：（是可正确运行得到结果的）

def deduplicate(lst):
    new_lst = []
    for i in lst:
        if i not in new_lst:
            new_lst.append(i)
    return new_lst

# 正确调用方式：
lst = [1, 2, 2, 3, 1]
result = deduplicate(lst)  # 接收返回值
print(result)  # 输出 [1, 2, 3]

代码实现CoT

文件引用包及版本信息：

pip install zhipuai==2.1.5.20250611;

具体代码实现：


from zhipuai import ZhipuAI
from dotenv import load_dotenv

# 加载环境变量（建议将API密钥放在.env文件中）
load_dotenv()

def glm_auto_cot(question):
    client = ZhipuAI()
    response = client.chat.completions.create(
        model="glm-4",  # 指定模型
        messages=[
            {"role": "user", "content": "请按步骤推理并解答问题，在最终答案前标注【答案】："},
            {"role": "assistant", "content": "好的，我会逐步推理并清晰展示思考过程"},
            {"role": "user", "content": question}
        ],
        temperature=0.3,  # 降低随机性保证推理严谨性
        top_p=0.7,
        max_tokens=1024
    )
    return response.choices[0].message.content

# 中国特色问题测试集
questions = [
    "《红楼梦》中贾宝玉、林黛玉、薛宝钗三人的年龄关系是怎样的？",
    "根据中国个人所得税法，月收入20000元需要缴纳多少税款？",
    "从北京到上海，高铁需要2.5小时，飞机需要1.5小时（含机场时间），哪种方式更高效？"
]

print("智谱GLM自动思维链演示".center(50, "="))
for i, q in enumerate(questions):
    result = glm_auto_cot(q)
    print(f"\n问题{i+1}: {q}")
    print(f"推理过程:\n{result}")
    print("-"*50)

总结与思考

零样本思维链提示，是一种巧妙的应用。它还有一种更好的应用技巧，这个是大佬们在研究自动提示工程师（APE，这个提示技术，我们后面再聊）的过程中发现的。在输入内容后，加上一行 “让我们一步一步地解决这个问题，以确保我们有正确的答案。”

思维链提示和前面所学的少样本提示结合，可以得到少样本CoT提示，它们的定义和原理对比分析：

维度	链式思考（CoT）提示	少样本提示
定义	通过提示引导模型模拟人类“分步思考”过程，逐步推导答案，强调推理过程的显式展示。	提供少量（1-5个）目标任务的输入-输出示例，通过示例示范引导模型学习任务模式。
核心原理	依赖模型的推理能力（如逻辑推导、因果分析），将复杂问题拆解为可理解的步骤，逐步推导结论。	依赖示例的模式注入（如格式、术语、逻辑），通过少量数据调整模型输出，使其符合目标任务要求。
知识来源	模型内置的通用知识（如数学定理、逻辑规则）或任务相关的先验信息（如科学原理）。	示例提供的领域知识或任务逻辑（如法律术语、代码语法、教学结构）。