深度解析——机器学习“照妖镜”：交叉验证如何让模型现出原形？

原创 已于 2025-09-27 06:47:29 修改 · 1.2k 阅读 · 30 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习 #人工智能 #深度学习

于 2025-09-27 06:39:14 首次发布

拓展参考文章请阅读

交叉验证是模型评估的黄金法则吗？当我们将场景从传统的机器学习切换到深度学习时，这一法则是否依然适用？为什么在实际的AI项目中，工程师们对待交叉验证的态度会有天壤之别？请阅读：交叉验证的不同命运：在机器学习与深度学习中的应用差异

本文前言

交叉验证（Cross-Validation）是一种重要的模型评估方法。在机器学习中，我们通常将数据集分为训练集和测试集。训练集用于训练模型，而测试集则用于评估模型在未知数据上的泛化能力。然而，如果我们只使用一次固定的训练集和测试集划分，评估结果可能会因为数据划分的偶然性而产生偏差。例如，如果测试集中的样本恰好比较简单，模型的性能可能被高估；反之，如果测试集比较难，模型的性能可能被低估。

交叉验证的核心思想是重复地将数据集划分为训练集和验证集（或称测试集），然后多次训练和评估模型，最后将多次评估结果的平均值作为最终的性能指标。这样做可以减少因数据划分而带来的偶然性，从而更稳定、更可靠地评估模型的泛化能力。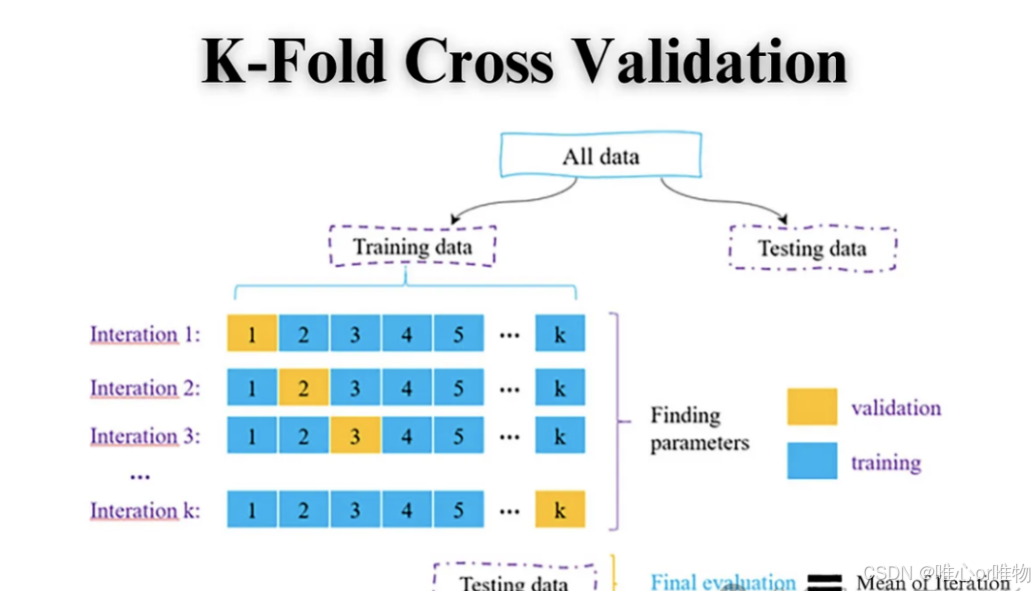

交叉验证的好处

  • 更可靠的性能评估

    传统的简单训练/测试集划分可能会因为划分的随机性而导致评估结果不稳定。交叉验证通过多次评估取平均，能更全面、更稳定地反映模型的泛化能力。

  • 充分利用数据

    在每次迭代中，数据集的每个样本都有机会成为训练数据，也有机会成为测试数据，这尤其对于数据量较少的情况非常有益。

  • 帮助选择模型和超参数

    交叉验证是超参数调优（如网格搜索、随机搜索）的基础。通过比较不同超参数组合在交叉验证中的平均得分，我们可以选择出最优的超参数。

常见的交叉验证算法

下面我将详细介绍几种常见的交叉验证算法。

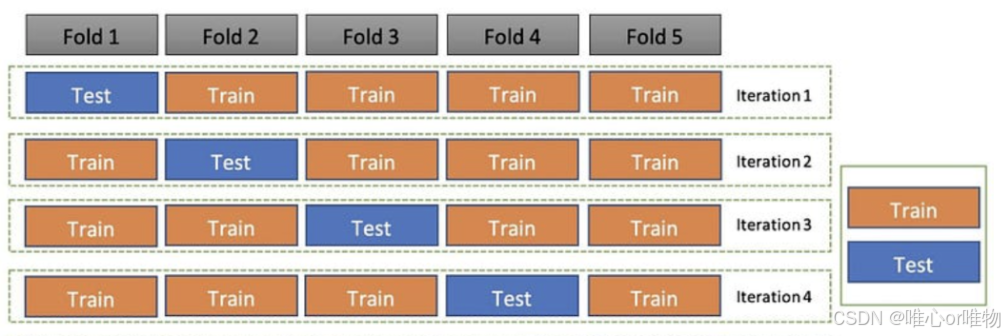
1. k 折交叉验证（k-Fold Cross-Validation）

这是最常用、最基础的交叉验证方法。

工作原理

  1. 将整个数据集随机分成 k 个大小相等的子集（或称为“折”）。

  2. 在每次迭代中，选择一个子集作为测试集，其余的  个子集作为训练集。

  3. 重复这个过程 k 次，确保每个子集都作为测试集使用过一次。

  4. 计算每次迭代的模型性能指标（如准确率、F1 分数等）。

  5. 最后，将这 k 次的性能指标取平均值作为模型的最终评估结果。

优缺点

  • 优点：简单易懂，计算效率相对较高，能有效利用数据。

  • 缺点：如果数据类别分布不均衡，随机划分可能会导致某些折中不包含所有类别，影响评估结果。

import numpy as np
from sklearn.model_selection import KFold
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
X, y = load_iris(return_X_y=True)

# 初始化模型
model = LogisticRegression(solver='liblinear')

# 定义 K 折交叉验证，这里 k=5
kf = KFold(n_splits=5, shuffle=True, random_state=42)

# 存储每次验证的准确率
accuracies = []

# 进行交叉验证
for train_index, test_index in kf.split(X):
    # 划分训练集和测试集
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    # 训练模型
    model.fit(X_train, y_train)

    # 在测试集上进行预测
    y_pred = model.predict(X_test)

    # 计算准确率并存储
    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)

# 打印每次的准确率和平均准确率
print("每次的准确率:", accuracies)
print("平均准确率:", np.mean(accuracies))
2. 分层 k 折交叉验证（Stratified k-Fold Cross-Validation）

这是对标准 K 折交叉验证的改进，主要用于处理类别不平衡的数据集。

它的核心是在划分数据时，确保每个折中的各类样本比例与整个原始数据集的类别比例保持一致。

例如，如果原始数据集中类别 A 占 80%，类别 B 占 20%，那么每个训练集和测试集中，A 和 B 的比例也将大致保持在 80% 和 20%。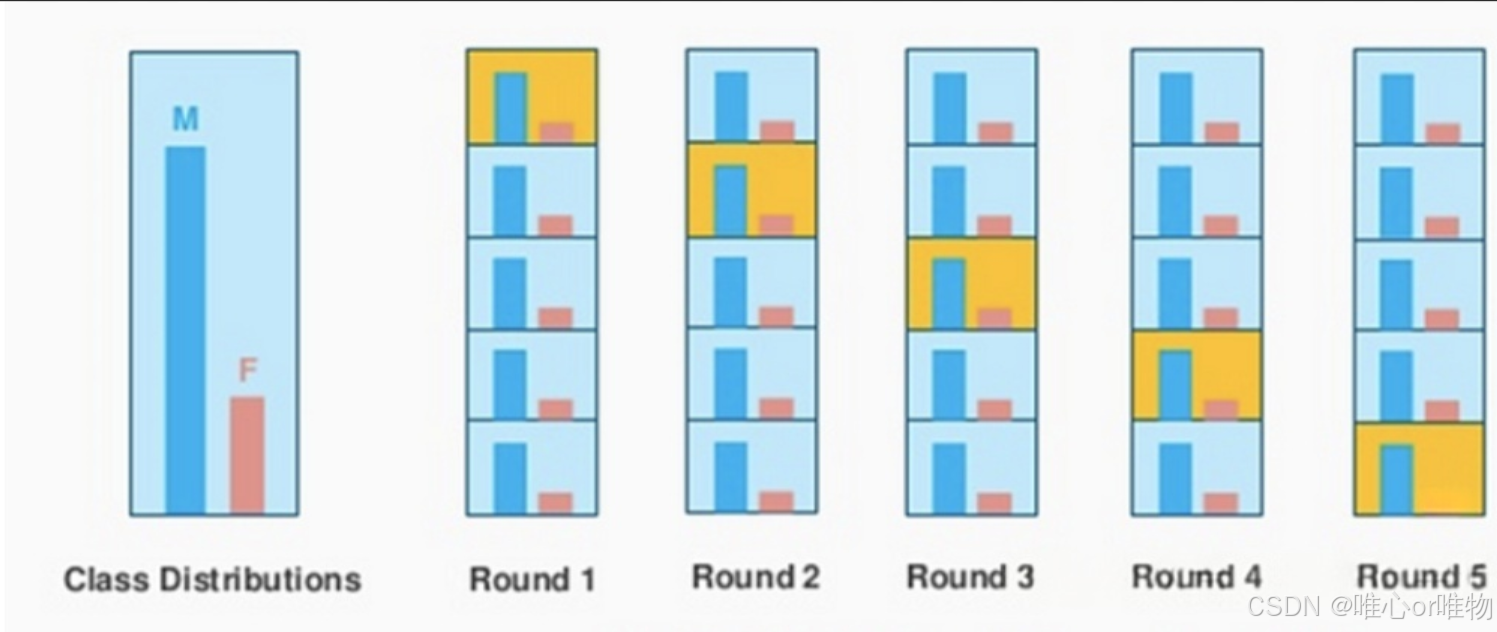

优缺点

  • 优点：解决了 k 折交叉验证在不均衡数据集上的问题，评估结果更具代表性，更稳定。

  • 缺点：相比标准 k 折，实现起来稍微复杂一些。

import numpy as np
from sklearn.model_selection import StratifiedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
X, y = load_iris(return_X_y=True)

# 初始化模型
model = LogisticRegression(solver='liblinear')

# 定义分层 K 折交叉验证，这里 k=5
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)

# 存储每次验证的准确率
accuracies = []

# 进行分层交叉验证
for train_index, test_index in skf.split(X, y):
    # 划分训练集和测试集
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    # 训练模型
    model.fit(X_train, y_train)

    # 在测试集上进行预测
    y_pred = model.predict(X_test)

    # 计算准确率并存储
    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)

# 打印每次的准确率和平均准确率
print("每次的准确率:", accuracies)
print("平均准确率:", np.mean(accuracies))
3. 留一交叉验证（LOOCV）

这是一种特殊的 k 折交叉验证，其中  等于数据集的样本总数 。

工作原理

  1. 每次只留一个样本作为测试集。

  2. 其余的  个样本作为训练集。

  3. 重复这个过程  次，直到每个样本都作为测试集使用过一次。

优缺点

  • 优点：每次训练几乎使用了所有数据，因此评估结果更接近模型在整个数据集上的表现。

  • 缺点：计算成本极高。如果数据集有 10000 个样本，就需要训练和评估模型 10000 次，这在实际应用中通常是不可行的。

import numpy as np
from sklearn.model_selection import LeaveOneOut
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
X, y = load_iris(return_X_y=True)

# 初始化模型
model = LogisticRegression(solver='liblinear')

# 定义留一交叉验证
loo = LeaveOneOut()

# 存储每次验证的准确率
accuracies = []

# 注意：LOOCV 对于大数据集非常慢，这里只是为了演示
for train_index, test_index in loo.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)

# 打印平均准确率
print("平均准确率:", np.mean(accuracies))
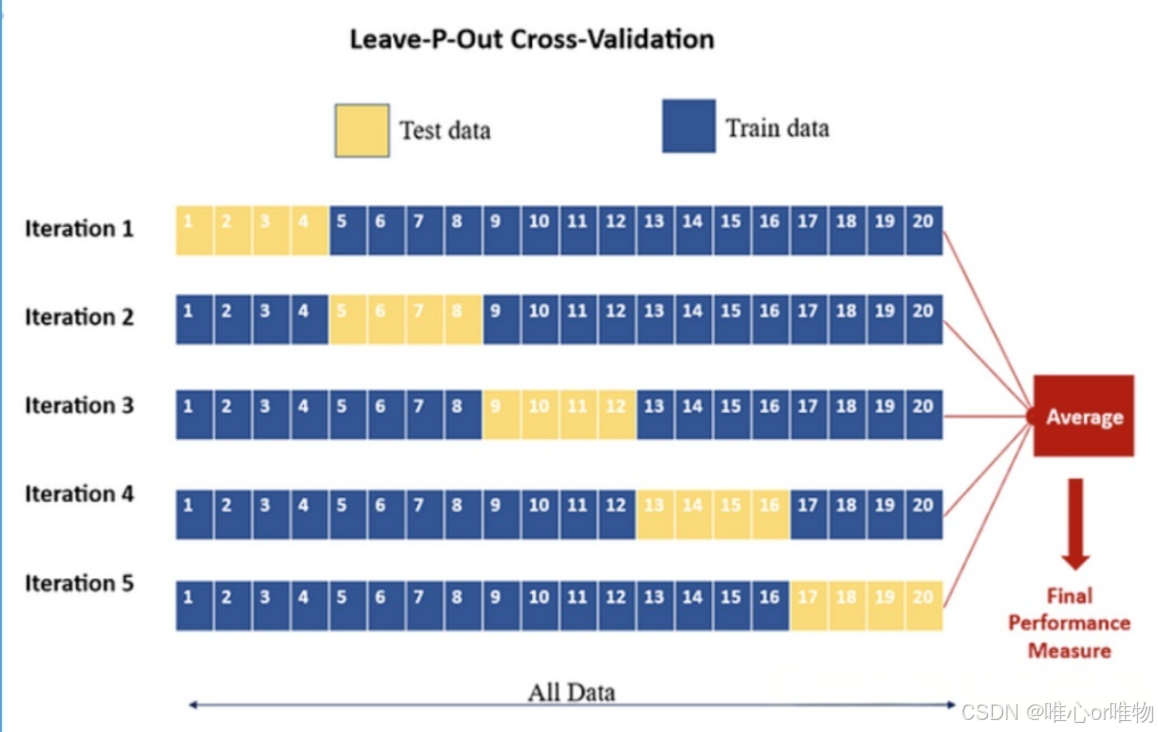
4. 留 p 交叉验证（LPOCV）

这是 LOOCV 的一个泛化版本，每次保留 p 个样本作为测试集，而剩余的样本作为训练集。

工作原理

  1. 每次从数据集中留出 p 个样本作为测试集。

  2. 其余  个样本作为训练集。

  3. 对所有可能的组合进行重复，直到所有  种组合都测试过。

优缺点

  • 优点：提供了比 LOOCV 更多的灵活性。

  • 缺点：计算成本爆炸式增长，随着数据集大小 N 和 p 的增大，可能的组合数量呈指数级增长，计算代价比 LOOCV 更高。因此在实际应用中很少使用。

import numpy as np
from sklearn.model_selection import LeavePOut
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
X, y = load_iris(return_X_y=True)

# 初始化模型
model = LogisticRegression(solver='liblinear')

# 定义留 p 交叉验证，这里 p=2
lpo = LeavePOut(p=2)

# 存储每次验证的准确率
accuracies = []

# 警告：此方法组合数量巨大，计算量指数级增长，请勿在大型数据集上运行
# 鸢尾花数据集共150个样本，C(150, 2) = 11175次迭代
# 仅作为示例，实际应用中很少使用
for train_index, test_index in lpo.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    accuracies.append(accuracy)

# 打印平均准确率
print("平均准确率:", np.mean(accuracies))
5.重复 k 折交叉验证（Repeated k-Fold Cross-Validation）

这是对标准 K 折交叉验证的扩展，通过重复多次 K 折过程来进一步提高评估的稳健性。

例如，“重复10次、5折交叉验证”意味着整个5折交叉验证过程会独立地重复10次，每次都有不同的随机划分。

最终的性能评估是这10次交叉验证结果的平均值。

工作原理

  1. 将 k 折交叉验证的过程重复 n 次。

  2. 最后，将所有  次的评估结果取平均值。

优缺点

  • 优点：评估结果比单次 k 折更稳定，降低了随机划分带来的影响。

  • 缺点：计算成本是标准 k 折的  倍。

import numpy as np
from sklearn.model_selection import RepeatedKFold
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.metrics import accuracy_score

# 加载鸢尾花数据集
X, y = load_iris(return_X_y=True)

# 初始化模型
model = LogisticRegression(solver='liblinear')

# 定义重复 K 折交叉验证
# n_splits=5 (5折)，n_repeats=10 (重复10次)
rkf = RepeatedKFold(n_splits=5, n_repeats=10, random_state=42)

# 存储所有折的准确率
all_accuracies = []

# 进行交叉验证
for train_index, test_index in rkf.split(X):
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    all_accuracies.append(accuracy)

# 打印所有准确率的平均值和标准差
print("总平均准确率:", np.mean(all_accuracies))
print("准确率的标准差:", np.std(all_accuracies))
6. 时间序列交叉验证（Time Series Cross-Validation）

在处理时间序列数据时，传统的随机交叉验证方法会破坏数据的时序依赖性，导致模型在评估时“偷看”了未来的信息。因此，我们需要使用专门的时间序列交叉验证方法。

常见的两种时间序列交叉验证方法

1.滚动交叉验证（Rolling Cross-Validation）

这是一种最常见也最直观的时间序列交叉验证方法。它通过固定训练集的大小，然后像一个“窗口”一样，在时间轴上向前滑动。

步骤

  1. 设置窗口大小：定义一个固定大小的训练窗口。例如，使用过去 12 个月的数据作为训练集。

  2. 首次训练与测试：用第一个窗口（例如第 1-12 个月）的数据训练模型，然后用紧随其后的下一段时间（例如第 13 个月）的数据进行测试。

  3. 滚动前进：将训练窗口向后滑动一步。例如，使用第 2-13 个月的数据作为新的训练集，用第 14 个月的数据进行测试。

  4. 重复：不断重复这个过程，直到窗口滑动到数据集的末尾。

示例

  • 假设我们有 100 天的数据，训练窗口大小为 60 天，测试窗口大小为 10 天。

  • 迭代 1：训练模型使用第 1-60 天的数据，评估模型使用第 61-70 天的数据。

  • 迭代 2：训练模型使用第 11-70 天的数据，评估模型使用第 71-80 天的数据。

  • 迭代 3：训练模型使用第 21-80 天的数据，评估模型使用第 81-90 天的数据。

2.扩展窗口交叉验证（Expanding Window Cross-Validation）

这种方法更加保守，它在每次迭代中不断扩展训练集，而不是保持其大小不变。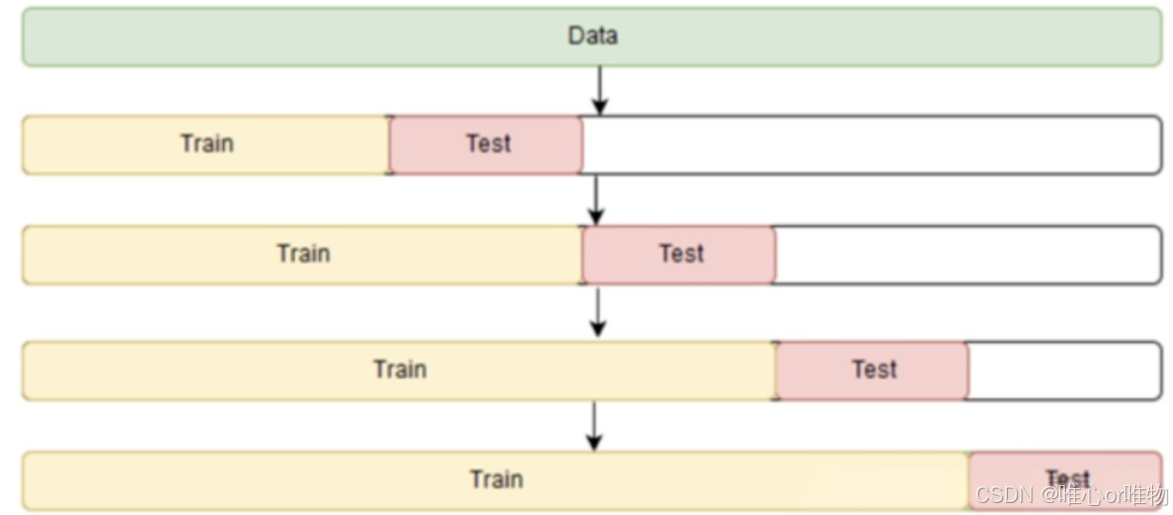

工作原理

  1. 首先，定义一个初始训练集大小和一个测试集大小。

  2. 第一次迭代：使用最早的一段数据作为初始训练集，其后的数据作为测试集。

  3. 第二次迭代：将第一次迭代的训练集和测试集都加入到新的训练集中，新的测试集是其后的下一段数据。

  4. 重复此过程，直到数据集结束。

示例

  • 假设我们有 100 天的数据，初始训练集为 60 天，测试窗口大小为 10 天。

  • 迭代 1：训练模型使用第 1-60 天的数据，评估模型使用第 61-70 天的数据。

  • 迭代 2：训练模型使用第 1-70 天的数据，评估模型使用第 71-80 天的数据。

  • 迭代 3：训练模型使用第 1-80 天的数据，评估模型使用第 81-90 天的数据。

import numpy as np
from sklearn.model_selection import TimeSeriesSplit
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 创建一个简单的模拟时间序列数据集
# X 是时间点，y 是随时间变化的数值
X = np.arange(100).reshape(-1, 1)  # 100个时间点
y = np.sin(X).ravel() + np.random.normal(0, 0.1, 100) # 一个带噪声的正弦曲线

# 初始化模型
model = LinearRegression()

# 定义时间序列交叉验证
# n_splits=5，表示有5个测试集，每次训练集会逐渐增长
tscv = TimeSeriesSplit(n_splits=5)

# 存储每次验证的均方误差
mses = []

# 进行交叉验证
for train_index, test_index in tscv.split(X):
    # 划分训练集和测试集
    X_train, X_test = X[train_index], X[test_index]
    y_train, y_test = y[train_index], y[test_index]

    # 打印划分情况，可以看到训练集在增长，测试集在滑动
    # print("训练集索引:", train_index)
    # print("测试集索引:", test_index)
    # print("-" * 20)

    # 训练模型
    model.fit(X_train, y_train)

    # 在测试集上进行预测
    y_pred = model.predict(X_test)

    # 计算均方误差并存储
    mse = mean_squared_error(y_test, y_pred)
    mses.append(mse)

# 打印每次的均方误差和平均均方误差
print("每次的均方误差:", np.round(mses, 4))
print("平均均方误差:", np.round(np.mean(mses), 4))
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值