AtentionUnet介绍

原创已于 2025-10-30 09:20:31 修改 · 511 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #Unet #AttentionUnet #语义分割

于 2025-10-10 11:30:01 首次发布

简介

AttentionUnet 是一种基于经典 U-Net 架构改进的医学图像分割模型，通过引入注意力机制（Attention Gate, AG）来增强模型对目标区域的聚焦能力，抑制无关背景信息的干扰。其主要改进集中在跳跃连接（Skip Connection）部分，通过注意力门控动态调整特征图的权重，提升分割精度。AttentionUnet网络结构如下图所示：

注：关于U-NET的讲解可以看博主的这篇文章

https://blog.youkuaiyun.com/qq_73038863/article/details/151991801?fromshare=blogdetail&sharetype=blogdetail&sharerId=151991801&sharerefer=PC&sharesource=qq_73038863&sharefrom=from_link

网络结构

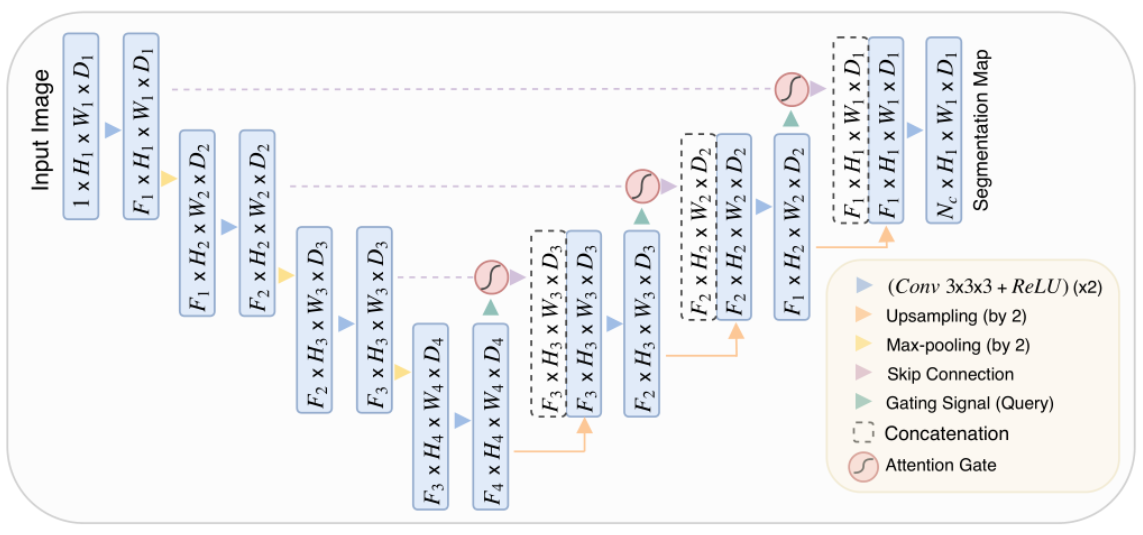
可以看出，AttentionUnet对于U-NET的改进点主要在于添加了注意力门控（Attention Gate）。在 U-Net 的跳跃连接中，编码器（下采样）的特征图会直接与解码器（上采样）的特征图拼接。

而在AttentionUnet 在拼接前加入注意力门控模块，动态计算编码器特征图的权重，加权处理后的编码器特征与解码器（上采样后的）特征拼接，替代原始 U-Net 的直接拼接。

这种机制能自动聚焦于目标区域，减少背景噪声的影响。也可以理解为抑制无关区域、突出目标结构。

AG的结构图如下图所示：

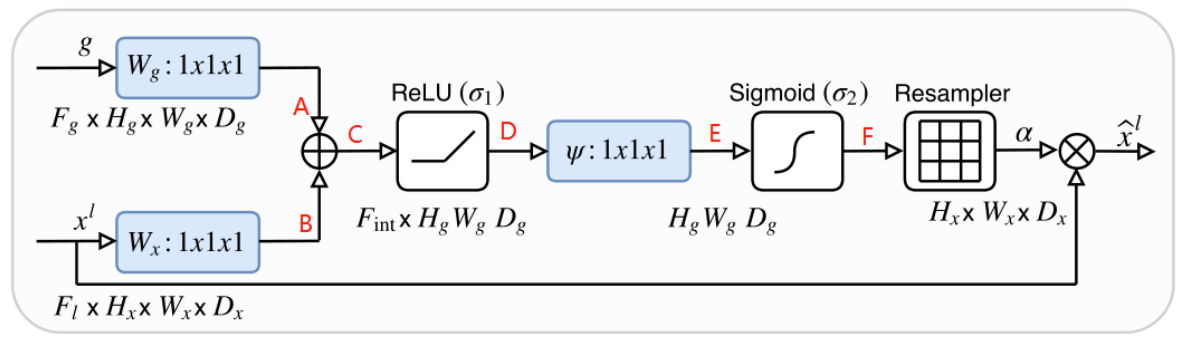
g和xl分别为skip connection的输出和下一层的输出。

示意图如下所示：

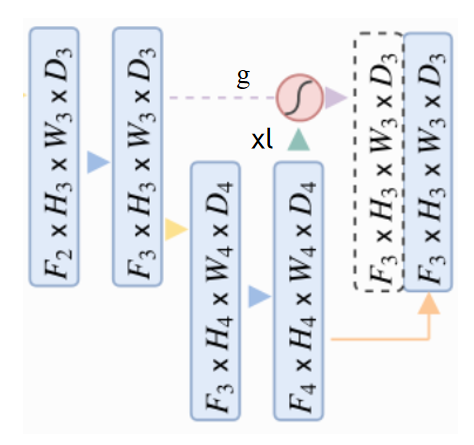
Wg和Wx经过相加，ReLU激活，1x1x1卷积，Sigmoid激活，生成一个权重信息，将这个权重与原始输入xl相乘，得到了对xl的attention激活。这就是Attenton Gate的思想。

简单代码示例

AG的简单代码示例（基于Pytorch框架）：

class AttentionGate(nn.Module):
    def __init__(self, in_channels, gating_channels):
        super().__init__()
        self.W_g = nn.Conv2d(gating_channels, in_channels, kernel_size=1)
        self.W_x = nn.Conv2d(in_channels, in_channels, kernel_size=1, stride=2)
        self.psi = nn.Conv2d(in_channels, 1, kernel_size=1)
        self.relu = nn.ReLU()
        self.sigmoid = nn.Sigmoid()

    def forward(self, x, g):
        g_conv = self.W_g(g)
        x_conv = self.W_x(x)
        combined = self.relu(g_conv + x_conv)
        attention = self.sigmoid(self.psi(combined))
        return x * attention