Java实现之普利姆(Prim)算法

一.问题引入

 

1.问题引入

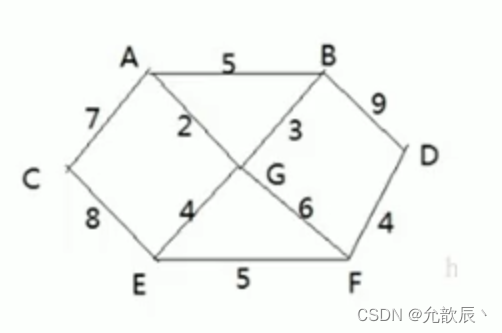
1)有胜利乡有7个村庄(A, B,C,D,E,F,G)，现在需要修路把7个村庄连通

2)各个村庄的距离用边线表示(权)，比如A-B距离5公里

3)问:如何修路保证各个村庄都能连通，并且总的修建公路总里程最短?

2.最小生成树

修路问题本质就是就是最小生成树问题，先介绍一下最小生成树(Minimum Cost Spanning Tree)，简称MST.
1） 给定一个带权的无向连通图,如何选取一棵生成树,使树上所有边上权的总和为
最小,这叫最小生成树

2)N个顶点，一定有N-1条边

3)包含全部顶点

4)N-1条边都在图.

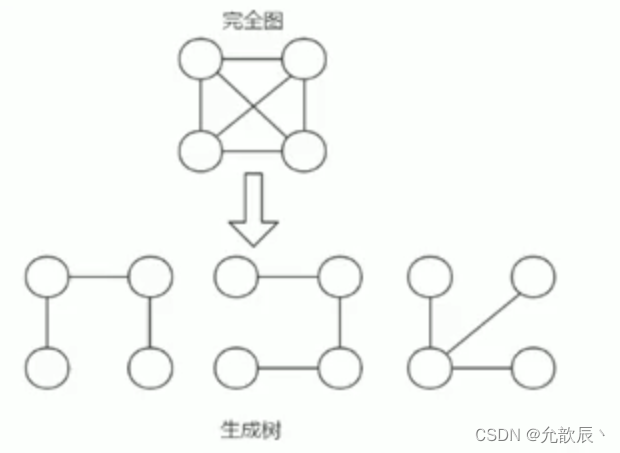
5)举例说明(如图)

6)求最小生成树的算法主要是普里姆
算法和克鲁斯卡尔算法

 

二.普利姆算法

1.基本介绍

1）普利姆(Prim)算法求最小生成树，也就是在包含n个顶点的连通图中，找出只有
(n-1)条边包含所有n个顶点的连通子图，也就是所谓的极小连通子图
2)普利姆的算法如下:
(1)设G=(V,E)是连通网，T=(U,D)是最小生成树，v,u是顶点集合，E,D是边的集合
(2)若从顶点u开始构造最小生成树，则从集合v中取出顶点u放入集合u中，标记顶点v的
visited[u]=1
(3若集合u中顶点ui与