编译原理——NFA转DFA实验全过程+实验代码

原创已于 2025-03-04 22:11:01 修改 · 2k 阅读

36 ·

CC 4.0 BY-SA版权

文章标签：

#编译原理 #实验

于 2024-10-14 14:18:54 首次发布

学习记录同时被 2 个专栏收录

100 篇文章

订阅专栏

编译原理

4 篇文章

订阅专栏

实验目的

设计并实现将NFA确定化为DFA的子集构造算法，从而更好地理解有限自动机之间地等价性，掌握词法分析器自动产生器的构造技术。该算法也是构造LR分析器的基础。

实验要求

设计并实现计算状态集合I的ε闭包的算法ε_Closure(I)和转化函数Move(I,a),并在此基础上实现子集构造算法Subset_Construction。利用该从NFA到DFA的转换程序Subset_Construction，任意输入一个NFA N=（S，Σ，δ,s0,F）,输出一个接收同一语言的DFA M=（S’，Σ，δ’,s0’,F’）。

实验内容

①实验原理

令I是NFA N的状态集S的一个子集，I的ε闭包的ε_Closure(I)构造规则如下：

若s∈I，则s∈ε_Closure(I)；
若s∈ε_Closure(I)且δ(s，ε)=s’而s’∉ε_Closure(I)，则s’ ∈ε_Closure(I)

根据上面的规则，下面给出了计算I的ε闭包的算法ε_Closure(I)。

SET S；

SET ε_Closure(input)

SET *input;

{

S=input;/*初始化*/

push(); /*把输入状态集中的全部状态压入栈中*/

while(栈非空){

Nfa_state i;

pop();/*把栈顶元素弹出并送入i*/

if(存在δ(i，ε)=j){

把i加到S中;

把j压入栈中;

}

return S;/*返回ε_Closure(input)集合*/

}

完成上述算法的设计。

令I是NFA N状态集S的一个子集，a∈Σ，转换函数Move(I,a)定义为：

Move(I,a)=ε_Closure(I)

其中，J={s’|s∈I且δ(s，ε)=s’}

转换函数Move(I,a)的设计通过调用ε_Closure(input)实现，完成该函数设计。

从NFA N构造一个与其等价的DFA M的子集构造算法，就是要为DFA M构造状态转换表Trans,表中的每个状态是NFA N状态的集合，DFA M将“并行” 地模拟NFA N面对输入符号串所有可能地移动。下面给出了子集构造算法 Subset_Construction的框架，请完成其设计过程。

有关数据结构：

States[] 是一个M的数组，每个状态有两个域，set域存放的状态集合，flg域为一标识。

Trans[] 是M的转移矩阵（输入字母表Σ元素个数×最大状态数），Trans[i][a]=下一状态。

i 代表M的当前状态号

a 代表输入符号，a∈Σ

Nstates[] M的下一新状态号

S 定义M的一个状态的N的状态集

初始化：

States[0].set=ε_Closure({N的初态})

States[0].flg=FALSE

Nstates=1

i=0

S=Ф

Trans初始化为无状态“-”

while(States[i]的flg为FALSE){

States[i].flg=TRUE;

for(每个输入符号a∈Σ){

S=ε_Closure(Move(States[i].set,a));

if(S非空)

if(States中没有set域等于S的状态){

States[Nstates].set=S;

States[Nstates].flg=FALSE;

Trans[i][a]=Nstates++;

}

else

Trans[i][a]=States中一个set域为S的下标；

}

此算法的输出M主要由Trans矩阵描述，其中省略每个状态是否为终态的描述，应加以完善。

（4）测试用例

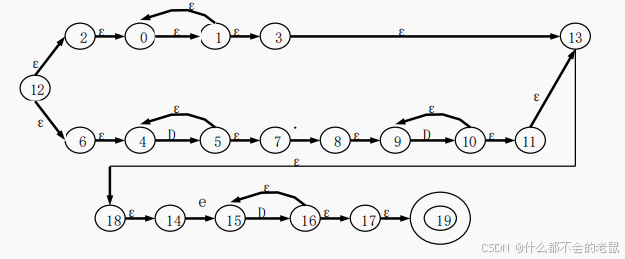
对下图所示的NFA N用子集构造算法Subset_Construction确定化。

NFA N的初态为12，DFA M的初态为ε_Closure（{12}）。

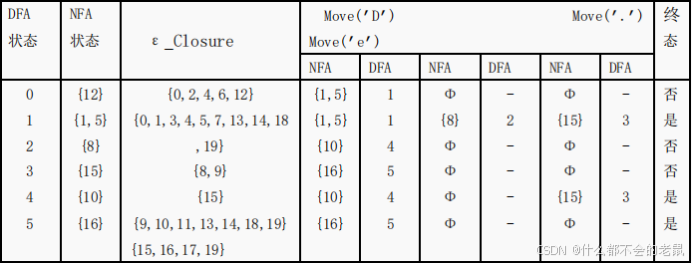
整个转换过程可用下表来概括。

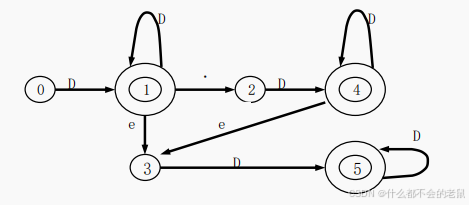
DFA M的状态转换图如下。

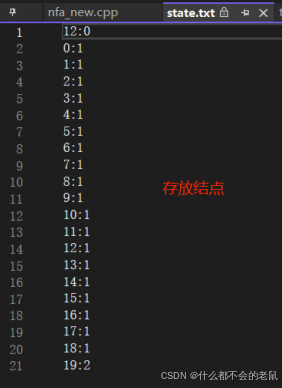
②state.txt(存放结点状态)

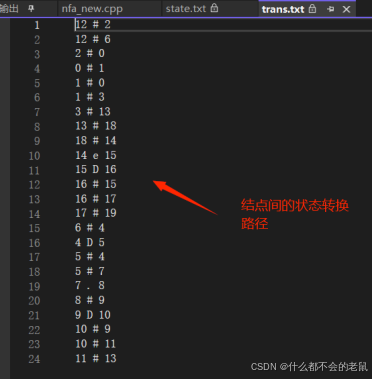
③trans.txt（存放结点间的状态转换路径）

④运行的实验结果：

实验代码

#include <iostream>
#include <fstream>
#include <set>
#include <queue>
#include <vector>
#include<string.h>
#define MAX 10
using namespace std;

//相关全局变量
std::set<int> NFASet;     //NFA状态集
set<char> charSet;        //接受字符集
vector<set<int>> DFASet;   //DFA状态集
int nfaNum, charsNum, dfaNum;
char** trans = nullptr;   //NFA状态转换表,由文件动态读入创建
char DFAGraph[MAX][MAX];  //DFA状态转换表
bool isEnd[MAX];   //DFA终止状态判断
//函数申明
void InitNfa(const char* path, int& startState, int& endState);  //nfa初始化
void InitTransMatrix(const char* path);  //状态转换表初始化
template <typename T>
void printTransMatrix(T trans, int num);    //格式化打印
void printSet(set<int> I);
set<int> getEClosure(set<int> I);   //空弧闭包
set<int> getMoveTo(set<int> I, char ac);   //ac字符闭包
int isSubset(set<int> I);  //判断I是否是DFASet的子集
void subsetConstruction(int startState, int endState);  //子集构造法确定DFA



int main() {

    set<int> DFAEndStates;
    int startState, endState;
    const char* statePath = "state.txt";  //结点
    const char* transPath = "trans.txt";  //状态转换

    //nfa状态集初始化
    InitNfa(statePath, startState, endState);
    nfaNum = NFASet.size();

    cout << "确定NFA初始值：" << endl;
    std::cout << "  NFA的状态总数：" << nfaNum << std::endl;
    cout << "  开始状态：" << startState << endl;
    cout<< "  结束状态：" << endState << endl;
   
    cout << endl;
    //NFA状态转换表
    cout << "NFA状态转换表：" << endl;
    InitTransMatrix(transPath);
    charsNum = charSet.size();  //接受字符集大小
    printTransMatrix(trans, nfaNum);
    cout << "状态转移的字符条件（除#）：" << ' ';
    for (const char& ac : charSet) { cout << ac << ' '; }
    cout << endl;
 
    //子集构造法确定DFA
    subsetConstruction(startState, endState);

    return 0;
}


void InitNfa(const char* path, int& startState, int& endState) {
    ifstream infile(path); // 打开文件
    if (!infile) {
        cerr << "文件打开错误！" << endl;
        return;
    }

    int state, flag;
    char ch;  // 分割符:
    while (infile >> state >> ch >> flag) { // 逐行读取数据
        NFASet.insert(state);
        if (flag == 0) { startState = state; }
        else if (flag == 2) { endState = state; };
    }
    infile.close();
}

void InitTransMatrix(const char* path) {
    ifstream infile(path); // 打开文件
    if (!infile) {
        cerr << "文件打开错误！" << endl;
        return;
    }

    trans = new char* [nfaNum];
    for (int i = 0; i < nfaNum; ++i) {
        trans[i] = new char[nfaNum + 1]; // +1 为了存储空字符'\0'
        for (int j = 0; j < nfaNum; ++j) {
            trans[i][j] = ' '; // 初始化为空格或其它占位符
        }
        trans[i][nfaNum] = '\0'; // 确保每行都是以空字符结尾的字符串
    }

    int startState, endState;
    char acceptChar;
    while (infile >> startState >> acceptChar >> endState) { // 逐行读取数据
        trans[startState][endState] = acceptChar;
        if (acceptChar != '#' and acceptChar) {
            //当acceptChar非空时加入字符集
            charSet.insert(acceptChar);
        }
    }
    infile.close();
}
template <typename T>
void printTransMatrix(T trans, int num) {
    // 打印表头
    printf("  "); // 空格用于对齐
    for (int j = 0; j < num; j++) {
        printf("%2d ", j); // 打印列号
    }
    printf("\n");
    // 打印分隔线
    for (int i = 0; i < num * 3.5; i++) {
        printf("-");
    }
    printf("\n");

    // 打印二维数组
    for (int i = 0; i < num; i++) {
        printf("%2d ", i); // 打印行号，加1是因为通常人们习惯从1开始计数
        for (int j = 0; j < num; j++) {
            printf("%c |", trans[i][j]); // 打印字符
        }
        printf("\n");
    }

    for (int i = 0; i < num * 3.5; i++) {
        printf("-");
    }
    printf("\n");

}
template <typename T>
void printTransMatrixx(T trans, int num) {
    // 打印表头
    printf("  "); // 空格用于对齐
    for (int j = 0; j < num; j++) {

        printf("%4d ", j); // 打印列号
    }
    printf("\n");
    // 打印分隔线
    for (int i = 0; i < num * 6; i++) {
        printf("-");
    }
    printf("\n");

    // 打印二维数组
    for (int i = 0; i < num; i++) {
        printf("%d ", i); // 打印行号，加1是因为通常人们习惯从1开始计数
        for (int j = 0; j < num; j++) {
           
            
            if (i == 1 && j == 2) { printf("     |"); }
            else if (i == 1 && j == 3) { printf("   %c|",trans[i][j]); }
            else if (i == 2 && j == 1) { printf("     |"); }
            else if (i == 2 && j == 2) { printf("     |"); }
            else if (i == 2 && j == 3) { printf("    |"); }
            else if (i == 2 && j == 4) { printf("   %c|", trans[i][j]); }
            else if (i == 3 && j == 1) { printf("     |"); }
            else if (i == 3 && j == 2) { printf("     |"); }
            else if (i == 3 && j == 3) { printf("    |"); }
            else if (i == 3 && j == 5) { printf("   %c|",trans[i][j]); }
            else if (i == 4 && j == 1) { printf("     |"); }
            else if (i == 4 && j == 2) { printf("     |"); }
            else if (i == 4 && j == 3) { printf("    |"); }
            else if (i == 4 && j == 4) { printf("   %c|",trans[i][j]); }
            else if (i == 4 && j == 5) { printf("    |"); }
            else if (i == 5 && j == 1) { printf("     |"); }
            else if (i == 5 && j == 5) { printf("    |"); }
            else{
            printf("    %c|", trans[i][j]);} // 打印字符
        }
        printf("\n");
    }

    for (int i = 0; i < num * 6; i++) {
        printf("-");
    }
    printf("\n");

}


void printSet(set<int> I) {
    for (const int& s : I) {
        cout << s << " ";
    }
    cout << endl;
}

/*计算I的eclosure集合*/
set<int> getEClosure(set<int> I) {                            //计算get_eclosure(I)集，方法广度优先搜索
    //拓扑排序算法
    std::vector<bool> visited(nfaNum, false);
   
    
    

    set<int> newSet;
    queue<int> Q;                                               //辅助队列

    for (set<int>::iterator it = I.begin(); it != I.end(); it++)       //复制当前集合并入队
    {
        Q.push(*it);
        newSet.insert(*it);
    }

    //类似图的广度遍历
    while (!Q.empty())                                           //队列每次弹出首位，并以首位进行扩展
    {
        int q = Q.front();
        Q.pop();                //扩展以后弹出
        for (int i = 0; i < nfaNum; i++)
        {
            if (trans[q][i] == '#' && !visited[i])
            {   //存在接受空弧"#"，从q->i
                newSet.insert(i);
                Q.push(i);
                visited[i] = true;                               //如果找到了，那么就加入新的set，并标记已访问
            }
        }
    }
    return newSet;
}

//计算字符ac的闭包
set<int> getMoveTo(set<int> I, char ac) {
    set<int> newSet;
    for (set<int>::iterator it = I.begin(); it != I.end(); it++)
    {
        int curState = *it;
        for (int i = 0; i < nfaNum; i++)
        {
            if (trans[curState][i] == ac)
                newSet.insert(i);
        }
    }
    return newSet;
}

//子集判断
int isSubset(set<int> st) {
    for (int i = 0; i < DFASet.size(); ++i) {
        if (DFASet[i] == st) {
            return i;  //是子集则返回集合在vector中的下标
        }
    }
    return -1;
}
//子集构造法确定NFA
void subsetConstruction(int startState, int endState) {
    memset(isEnd, false, MAX);
    set<int> cur;  //当前状态集合
    //将初始结点加入cur集合中，并求出其空弧闭包，得出初始状态集合
    cur.insert(startState);
    cur = getEClosure(cur);
    DFASet.push_back(cur);  //加入DFA状态集合
 
    cout << "NFA确定化的开始状态集合：";
    printSet(cur);
    cout << endl;

    //循环构造并不断更新DFASet
    for (int i = 0; i < DFASet.size(); ++i) {
        cur = DFASet[i];
        for (const char& ch : charSet) {
            set<int> newSet;
            newSet = getEClosure(getMoveTo(cur, ch));  //寻找ch字符的闭包的空弧闭包
            if (!newSet.empty()) {
                //输出闭包
                cout << "对应DFA状态的重新编号的闭包：" << i << "\t{";
                for (const int& st : DFASet[i]) {
                    cout << st << ",";
                }
                cout << "} | " << ch << " closure: ";
                printSet(newSet);
            }
            if (!newSet.empty()) {
                int idx = isSubset(newSet);  //该闭包是否包含于DFASet
                if (idx == -1) {
                    //如果结果集合不是DFASet的子集且非空，则加入
                    DFASet.push_back(newSet);
                    int len = DFASet.size();
                    DFAGraph[i][len - 1] = ch;  //从DFA的第i状态输入字符ch转换成第len-1状态，即刚插入进去的状态

                    if (newSet.count(endState) > 0) {
                        //终止结点属于该集合->其是DFA终止状态
                        isEnd[len - 1] = true;
                    }

                }
                else {
                    //是子集，从i->idx
                    DFAGraph[i][idx] = ch;
                }
            }
        }
        cout << "是不是结束状态(0：不是；1：是)：" << isEnd[i] << endl;
     
        cout << endl;
    }
    cout << endl;
    dfaNum = DFASet.size();
    cout << "DFA的状态转移矩阵：" << endl;
    printTransMatrixx(DFAGraph, dfaNum);

}