文章目录
- PART \textbf{PART } PART Ⅰ: 导论与预备知识
- 1. \textbf{1. } 1. 导论
- 2. GPU \textbf{2. GPU} 2. GPU架构与 CUDA \textbf{CUDA} CUDA编程模型
- PART \textbf{PART } PART Ⅱ: BANG \textbf{BANG} BANG的设计
- 1. BANG \textbf{1. BANG} 1. BANG的总体设计
- 2. BANG \textbf{2. BANG} 2. BANG的微内核设计与并行优化
-
- 2.0. \textbf{2.0. } 2.0. 微内核总体设计概览
- 2.1. \textbf{2.1. } 2.1. 第一阶段: PQ \textbf{PQ} PQ表的构建微内核
- 2.2. {}{}\textbf{2.2. } 2.2. 第二阶段: 主循环的主要内核 + \textbf{+} +并行优化
-
- 2.2.1. \textbf{2.2.1. } 2.2.1. 中 GPU \textbf{GPU} GPU阶段的 GPU \textbf{GPU} GPU微内核
-
- 2.2.1.1. \textbf{2.2.1.1. } 2.2.1.1. Bloom Filter \textbf{Bloom Filter} Bloom Filter微内核: 为 N i N_i Ni过滤已访问点
- 2.2.1.2. \textbf{2.2.1.2. } 2.2.1.2. 并行距离计算微内核: 计算 N i ′ {}N_i' Ni′集中所有邻居离查询点的距离
- 2.2.1.3. \textbf{2.2.1.3. } 2.2.1.3. 并行归并排序微内核: 为 N i ′ N_i^{'} Ni′集中所有邻居排序
- 2.2.1.4. \textbf{2.2.1.4. } 2.2.1.4. 列表合并微内核: 合并已排序的 N i ′ \mathcal{N}_i^{'} Ni′与当前工作列表 L i \mathcal{L}_i Li
- 2.2.2. \textbf{2.2.2. } 2.2.2. 中 GPU \textbf{GPU} GPU阶段的(非内核)并行优化
- 2.3. \textbf{2.3. } 2.3. 第三阶段: 实现重排的微内核
- 3. BANG \textbf{3. BANG} 3. BANG的不同版本
- PART \textbf{PART } PART Ⅲ: 实验验证与结论
- 1. \textbf{1. } 1. 实验设置
- 2. \textbf{2. } 2. 实验结果
- 3. \textbf{3. } 3. 结论
原论文: BANG: Billion-Scale Approximate Nearest Neighbor Search using a Single GPU
PART \textbf{PART } PART Ⅰ: 导论与预备知识
1. \textbf{1. } 1. 导论
1.1. \textbf{1.1. } 1.1. 关于 ANN \textbf{ANN} ANN
1️⃣高维 k k k最邻近查询
- 精确查询 (NN) \text{(NN)} (NN):
- 含义:找到与给定查询点最近的 k k k个数据点
- 困难:由于维度诅咒 → \to →难以摆脱暴力扫描 O ( n ∗ dimension ) O(n*\text{dimension}) O(n∗dimension)的复杂度
- 近似查询 (ANN) \text{(ANN)} (ANN):
- 核心:通过牺牲准确性来换取速度,以减轻维度诅咒
- On GPU \text{On GPU} On GPU:大规模并行处理可以提高 ANN \text{ANN} ANN吞吐量(固定时间内的查询数量)
- 基于图的 ANN \text{ANN} ANN:
- 处理大规模数据最为高效的 ANN \text{ANN} ANN方法
- Vamana/DiskANN \text{Vamana/DiskANN} Vamana/DiskANN是目前最先进的基于图的 ANN \text{ANN} ANN(详细的设计 Click Here \text{Click Here} Click Here)
1.2. \textbf{1.2. } 1.2. ANN \textbf{ANN} ANN的 GPU \textbf{GPU} GPU实现难点
1️⃣ GPU \text{GPU} GPU的内存有限
- 含义:目前主流 GPU \text{GPU} GPU内存有限,无法将构建好的图结构完整载入
- 现有方案:
方案 描述 缺陷 文献 分片 将图分片 → \to →不断在 CPU ⇆ GPU \text{CPU}\leftrightarrows{}\text{GPU} CPU⇆GPU交换片以处理整个图 PCIe \text{PCIe} PCIe带宽不够 GGNN \text{GGNN} GGNN 多 GPU \text{GPU} GPU 将图有效分割到所有 GPU \text{GPU} GPU上以容纳并处理整个图 硬件成本高 SONG \text{SONG} SONG/ FAISS \text{FAISS} FAISS 压缩 压缩图数据维度使图结构能北方进 GPU \text{GPU} GPU内存 召回率下降(只适合小数据) GGNN \text{GGNN} GGNN 2️⃣最有硬件使用
- GPU ⇆ CPU \text{GPU}\leftrightarrows{}\text{CPU} GPU⇆CPU负载平衡:确保二者持续并行工作不空闲,并且数据传输量不超过 PCIe \text{PCIe} PCIe极限
- 主存占用:基于 GPU \text{GPU} GPU的 ANN \text{ANN} ANN搜索占用的内存显著增加
1.3. BANG \textbf{1.3. BANG} 1.3. BANG的总体优化思路
1️⃣硬件优化
- 总线优化:减少 CPU-GPU \text{CPU-GPU} CPU-GPU间 PCIe \text{PCIe} PCIe的通信量 → \to →提高吞吐
优化思路 具体措施 减少(总共的)总线传输次数 负载平衡,预取/流水线(让 CPU/GPU \text{CPU/GPU} CPU/GPU尽量没空闲时间) 降低(一次的)总线传输量 传输 PQ \text{PQ} PQ压缩后的向量(而非原始向量) - GPU \text{GPU} GPU内存优化:避免存放图结构 + + +只存放 PQ \text{PQ} PQ压缩后的向量
2️⃣计算优化
- 加速遍历/搜索:使用 Bloom \text{Bloom} Bloom过滤器,快速判断 a ∈ A a\text{∈}A a∈A式命题的真伪
- 加速距离计算:使用 PQ \text{PQ} PQ压缩后的向量计算距离
3️⃣软件优化:设立微内核,将距离计算/排序/更新表操作拆分成更原子化的操作,以提高并行化
2. GPU \textbf{2. GPU} 2. GPU架构与 CUDA \textbf{CUDA} CUDA编程模型
2.1. GPU \textbf{2.1. }\textbf{GPU} 2.1. GPU体系结构
1️⃣计算单元组织架构

结构 功能 CUDA \text{CUDA} CUDA核心 类似 ALU \text{ALU} ALU(但远没 CPU \text{CPU} CPU的灵活),可执行浮点运算/张量运算/光线追踪(高级核心) Warp \text{Warp} Warp 多核心共用一个取指/译码器,按 SIMT \text{SIMT} SIMT工作(所有线程指令相同/数据可不同) SM \text{SM} SM 包含多组 Warps \text{Warps} Warps,所有 CUDA \text{CUDA} CUDA核心共用一套执行上下文(缓存) & \& &共享内存 2️⃣存储层次架构:

- 不同 SM \text{SM} SM能够 Access \text{Access} Access相同的 L2 Cache \text{L2 Cache} L2 Cache
- 显存与缓存之间的带宽极高,但是相比 GPU \text{GPU} GPU的运算能力仍然有瓶颈
2.2. \textbf{2.2. } 2.2. CUDA \textbf{CUDA} CUDA编程模型
1️⃣ CUDA \text{CUDA} CUDA程序简述
- CUDA \text{CUDA} CUDA程序的两部分
程序 运行位置 主要职责 Host程序CPU \text{CPU} CPU 任务管理/数据传输/启动 GPU \text{GPU} GPU内核 Device程序GPU \text{GPU} GPU 执行内核/处理数据 - Kernel \text{Kernel} Kernel即在 GPU \text{GPU} GPU上运行的函数,如下简单内核定义示例
//通过__global__关键字声名内核函数 __global__ void VecAdd(float* A, float* B, float* C) { int i = threadIdx.x; C[i] = A[i] + B[i]; } int main() { //通过<<<...>>>中参数指定执行kernel的CUDA thread数量 VecAdd<<<1, N>>>(A, B, C); }2️⃣线程并行执行架构
- 线程层次:
结构 地位 功能 Thread \text{Thread} Thread 并行执行最小单元 执行 Kernel \text{Kernel} Kernel的一段代码 Warp(32Threads) \text{Warp(32Threads)} Warp(32Threads) 线程调度的基本单位 所有线程以 SIMD \text{SIMD} SIMD方式执行相同指令 Block \text{Block} Block GPU \text{GPU} GPU执行线程基本单位 使块内线程内存共享/指令同步 Grid \text{Grid} Grid 并行执行的最大单元 执行整个内核(启动内核时必启动整个 Grid \text{Grid} Grid) - 线程在计算单元的映射:线程层次 ↔ 层次对应 GPU \xleftrightarrow{层次对应}\text{GPU} 层次对应 GPU物理架构

- 注意 SM \text{SM} SM和 Block \text{Block} Block不必 1v1 \text{1v1} 1v1对应也可 Nv1 \text{Nv1} Nv1对应
- 线程在存储单元的映射
线程结构 可 Access \textbf{Access} Access的内存结构 访问速度 Thread \text{Thread} Thread 每线程唯一的 Local Memory \text{Local Memory} Local Memory 极快 Block \text{Block} Block 每块唯一的 Shared Memory \text{Shared Memory} Shared Memory(块中每个线程都可访问) 较快 所有线程 唯一且共享的 Global Memory \text{Global Memory} Global Memory 较慢 2.3. CPU \textbf{2.3. CPU} 2.3. CPU与 GPU \textbf{GPU} GPU

1️⃣ CPU/GPU \text{CPU/}\text{GPU} CPU/GPU结构对比
GPU \text{GPU} GPU CPU \text{CPU} CPU ALU \text{ALU} ALU 功能强但数量少(只占 GPU \text{GPU} GPU小部),时钟频率极高 功能弱但数量大,时钟频率低 Cache \text{Cache} Cache 容量大并分级,缓存后续访问数据 容量很小,用于提高线程服务 控制 复杂串行逻辑,如流水/分支预测/乱序执行 简单(但大规模)并行逻辑 3️⃣ CPU ↔ 数据 / 指令传输 PCIe GPU \text{CPU} \xleftrightarrow[数据/指令传输]{\text{PCIe}} \text{GPU} CPUPCIe 数据/指令传输GPU交互
设备 逻辑地位 IO \textbf{IO} IO模块 任务分配 GPU \text{GPU} GPU 外设 IO Block \text{IO Block} IO Block(南桥) 控制逻辑和任务调度 CPU \text{CPU} CPU 主机 Copy Engine \text{Copy Engine} Copy Engine 执行大量并行计算任务
PART \textbf{PART } PART Ⅱ: BANG \textbf{BANG} BANG的设计
1. BANG \textbf{1. BANG} 1. BANG的总体设计
1.1. BANG \textbf{1.1. BANG} 1.1. BANG的索引架构
1.1.1. \textbf{1.1.1. } 1.1.1. BANG \textbf{BANG} BANG索引(硬件)布局
结构 功能 RAM \text{RAM} RAM 存放 Vamana \text{Vamana} Vamana算法构建的图结构 + + +数据点 GPU \text{GPU} GPU内存 存放 Vamana \text{Vamana} Vamana算法构建的图中点经过 PQ \text{PQ} PQ压缩后的向量 CPU-GPU \text{CPU-GPU} CPU-GPU总线 传输压缩向量 & \& &协调并行 1.1.2. BANG \textbf{1.1.2. BANG} 1.1.2. BANG索引构建算法: Vamana \textbf{Vamana} Vamana图
1️⃣ Vamana \text{Vamana} Vamana图构建基本操作
- 图查询算法:贪心搜索 GreedySearch ( s , x q , k , L ) \text{GreedySearch} \left(s, \mathrm{x}_q, k, L\right) GreedySearch(s,xq,k,L)
- 图剪枝算法:健壮性剪枝 RobustPrune ( p , R , α , L ) \text{RobustPrune}(p, R, \alpha, L) RobustPrune(p,R,α,L)
2️⃣ Vamana \text{Vamana} Vamana图构建总体流程

1.1.3. BANG \textbf{1.1.3. BANG} 1.1.3. BANG索引构建方法: 类似 DiskANN \textbf{DiskANN} DiskANN架构
1️⃣构建步骤:面向面向内存空间的优化
- 划分:用 k -means k\text{-means} k-means将 P P P分为多簇(每簇有一中心),再将 P P P所有点分给 ℓ > 1 \ell\text{>}1 ℓ>1个中心以构成重叠簇
- 索引:在每个重叠簇中执行 Vamana \text{Vamana} Vamana算法,构建相应有向边
- 合并:将所有构建的有向边合并在一个图中,完成构建
2️⃣关于重叠分簇:为了保证图的连通性,以及后续搜索的 Navigable \text{Navigable} Navigable
1.2. BANG \textbf{1.2. BANG} 1.2. BANG的查询架构
1.2.1. \textbf{1.2.1. } 1.2.1. 第一阶段: 初始化 &PQ \textbf{\&PQ} &PQ表的构建
1️⃣执行的操作
- 并行化:为查询集 Q ρ Q_\rho Qρ中的每个查询 { q 1 , q 2 , . . . , q ρ } \{q_1,q_2,...,q_{\rho}\} { q1,q2,...,qρ}分配一个独立的 CUDA \text{CUDA} CUDA线程 Block \text{Block} Block
- 距离表:在每个线程块上为每个 q i q_i qi计算并构建 PQ \text{PQ} PQ距离子表,最终合并 ρ \rho ρ个子表为距离表
- 搜索起点:每个 q i q_i qi从图质心开始,即 CPU ← 传输给 WorkList ← 放入 u i ∗ (当前/候选点) ← 初始化 Centroid \text{CPU}\xleftarrow{传输给}\text{WorkList}\xleftarrow{放入}\textbf{u}_i^*\textbf{(当前/候选点)}\xleftarrow{初始化}\text{Centroid} CPU传输给WorkList放入ui∗(当前/候选点)初始化Centroid
2️⃣ PQ \text{PQ} PQ表构建的时序逻辑
时期 操作 查询开始前 将查询点送入 GPU \text{GPU} GPU的 Copy \text{Copy} Copy引擎,在 CUDA \text{CUDA} CUDA核心上计算/构建/存储距离表 查询开始后 保留距离表在 GPU \text{GPU} GPU上直到查询结束 1.2.2. \textbf{1.2.2. } 1.2.2. 第二阶段: 并行 GreedySearch \textbf{GreedySearch} GreedySearch主循环
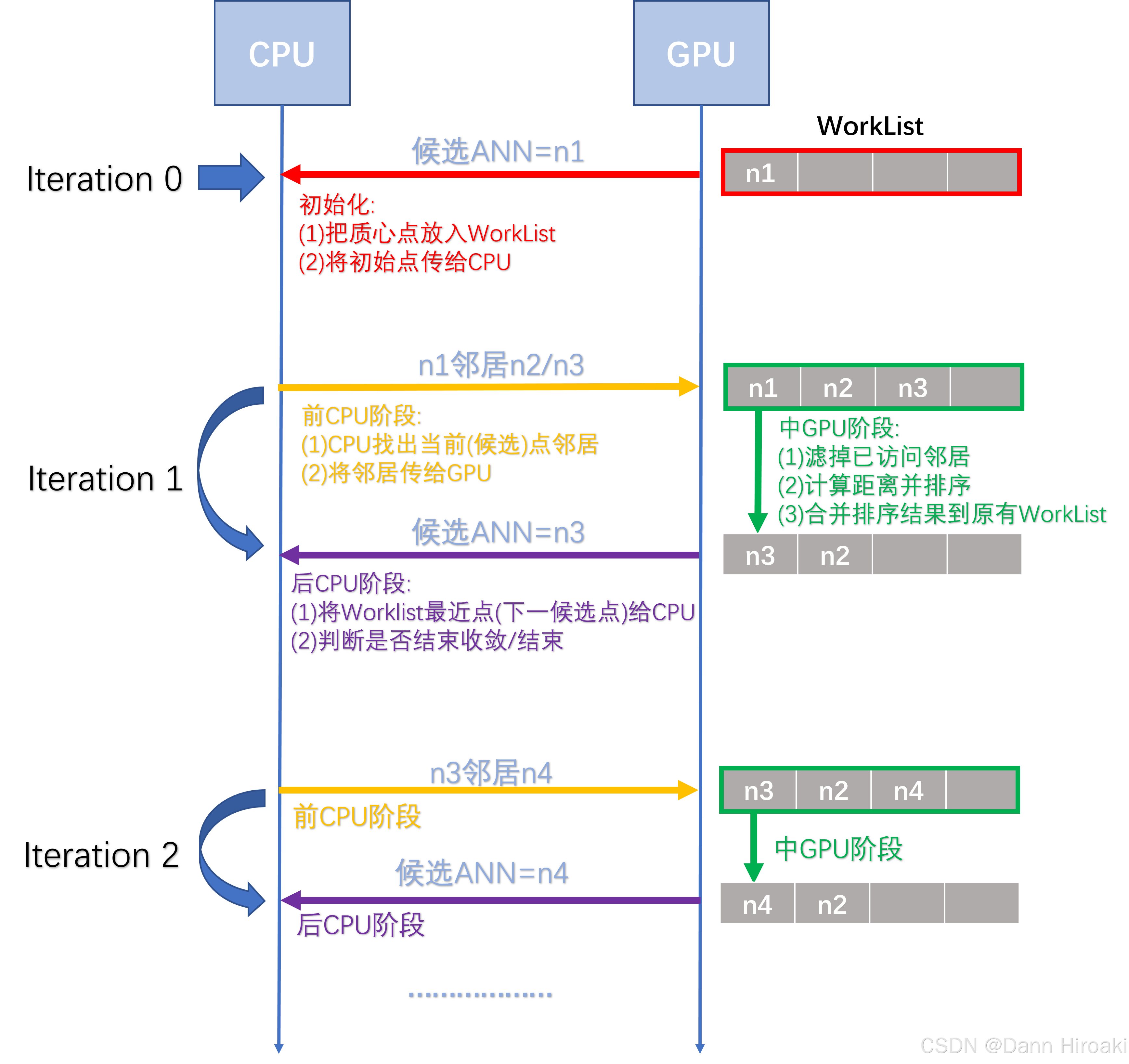
1️⃣前 CPU \text{CPU} CPU阶段: CPU \text{CPU} CPU从内存中获取当前在处理节点 u i ∗ u_i^* ui∗的邻居集 N i N_i Ni
🔁数据传输: CPU → 邻居集 N i GPU \text{CPU}\xrightarrow{邻居集N_i}\text{GPU} CPU邻居集NiGPU
2️⃣中 GPU \text{GPU} GPU阶段:接收 u i ∗ u_i^* ui∗的邻居集 N i N_i Ni后,并行地执行内核 & \text{\&} &全精度向量的异步传输
- 执行内核:按顺序执行以下内核及操作
步骤 操作 内核与否 过滤邻居 用 Bloom \text{Bloom} Bloom并行检查 ∀ n ∈ N i \forall{}n\text{∈}N_i ∀n∈Ni中未被访问点 → \to →并放入 N i ′ {}N_i' Ni′(未访问集) + \text{+} +更新 Bloom \text{Bloom} Bloom ✔️ 距离计算 用 PQ \text{PQ} PQ距离表并行计算所有未处理邻居 n k ∈ N i ′ {}n_k\text{∈}N_i' nk∈Ni′与查询点 q i q_i qi距离,并存在 D i [ k ] \mathcal{D}_i[k] Di[k] ✔️ 邻居排序 将 N i ′ {}N_i' Ni′和 D i [ k ] \mathcal{D}_i[k] Di[k]按与 q i q_i qi的距离执行归并排序,得到排序后的距离 D i ′ \mathcal{D}_i' Di′和节点 N i ′ \mathcal{N}_i' Ni′ ✔️ 合并列表 合并当前 WorkLisk ( L i ) \text{WorkLisk}(\mathcal{L}_i) WorkLisk(Li)与新排序的节点列表 N i ′ \mathcal{N}_i' Ni′形成新的 L i \mathcal{L}_i Li ✔️ 更新节点 又将 L i \mathcal{L}_i Li排序后选取最近的未访问点 u i ∗ {}u_i^* ui∗作为下一个当前节点 ❌ - 异步传输:执行内核的同时, CPU \text{CPU} CPU将 u i ∗ u_i^* ui∗的全精度向量传输给 GPU \text{GPU} GPU → \to →以便后续重排
🔁数据传输: CPU ← 当前节点 u i ∗ GPU \text{CPU}\xleftarrow{当前节点u_i^*}\text{GPU} CPU当前节点ui∗GPU
3️⃣后 CPU \text{CPU} CPU阶段:若 L i \mathcal{L}_i Li中所有点都被访问过且 ∣ L i ∣ = t |\mathcal{L}_i|\text{=}t ∣Li∣=t,则认为已经收敛 → \to →结束循环
1.2.3. \textbf{1.2.3. } 1.2.3. 第三阶段: (搜索收敛后的)重排与输出
1️⃣重排与输出
- 重排的时序逻辑
时间 操作 位置 搜索过程中 用一个数据结构,存储每个 Iter \text{Iter} Iter中向 CPU \text{CPU} CPU发送的全精度候选点 CPU→GPU \text{CPU→GPU} CPU→GPU 搜索完成后 计算所有候选点到查询点距离,按全精度距离排序后选取前若干 GPU \text{GPU} GPU - 输出:选取重排后的 L i \mathcal{L}_i Li中,离 q i q_i qi最近的 k k k个节点 → \to →作为 k - k\text{-} k-最邻近返回
2️⃣重排的意义:用小成本(仅极小部分即候选点以全精度送往 GPU \text{GPU} GPU),补偿由压缩距离产生的误差
2. BANG \textbf{2. BANG} 2. BANG的微内核设计与并行优化
2.0. \textbf{2.0. } 2.0. 微内核总体设计概览
1️⃣设立独立微内核的操作:
阶段 有独立微内核的操作 第一阶段(建表) PQ \text{PQ} PQ表构建操作 第二阶段(主查询) 过滤邻居,距离计算,邻居(归并)排序,归并列表 第三阶段(重排) 重排操作 2️⃣动态线程块的优化:
- 每个查询分配到一线程块执行,查询过程会依次执行多个内核
- 执行不同内核时按经验调整线程块大小(如计算密集型内核的块更大),以保证 GPU \text{GPU} GPU的高占有
2.1. \textbf{2.1. } 2.1. 第一阶段: PQ \textbf{PQ}







 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2162
2162










