本文概述了简单排序算法如选择排序、冒泡排序、桶排序和插入排序的基本原理和实现，以及快速排序、归并排序和希尔排序的高效排序方法。通过实例演示和代码展示，揭示这些算法在不同场景的应用和优劣。
简单排序算法
简单排序算法包括选择排序、冒泡排序、桶排序和插入排序
选择排序
- 基本思想
每一次从待排序的数据元素中选出最小（或最大）的一个元素，按照顺序放在待排序的数列的最前，直到全部待排序的数据元素排完。
- 排序过程
初始：[5 4 6 8 7 1 2 3]
第一趟排序后 1 [4 6 8 7 5 2 3]
第二趟排序后 1 2 [6 8 7 5 4 3]
第三趟排序后 1 2 3 [8 7 5 4 6]
第四趟排序后 1 2 3 4 [7 5 8 6]
第五趟排序后 1 2 3 4 5 [7 8 6]
第六趟排序后 1 2 3 4 5 6 [8 7]
第七趟排序后 1 2 3 4 5 6 7 [8]
最后排序结果 1 2 3 4 5 6 7 8
代码实现：
import java.util.Scanner;
import java.util.Stack;
public class Main {
static void select_Sort(int a[])
{
int n=a.length;
for (int i=0;i<n;i++)
{
int k=i;
for(int j=i+1;j<n;j++)
{
if(a[j]<a[k]) k=j;
}
if(k!=i) {
int temp = a[i];
a[i] = a[k];
a[k] = temp;
}
}
}
public static void main(String[] args)
{
int a[] =new int []{5 ,4 ,6 ,8 ,7, 1, 2 ,3};
select_Sort(a);
for(Object c:a)//遍历数组的简单方式 for (循环变量类型 循环变量名称 : 要被遍历的对象) 循环体
System.out.print(c+" ");
}
}
冒泡排序
- 基本思想
所谓冒泡排序就是依次将两个相邻的数进行比较，大的在前面，小的在后面。
即先比较第一个数和第二个数，大数在前，小数在后，然后比较第 2 个数和第 3 个数，直到比较最后两个数
第一次排序结束后，最小数的数一定在最后；第二次排序在第一趟的基础上重复上述操作
由于排序过程中总是大数在前，小数在后，相当于气泡上升，所以叫冒泡排序。
大数在前，小数在后排序后得到的是降序；小数在前，大数在后排序后得到的是升序结果
- 排序过程(降序)
初始数据：4 5 6 1 2 3
第一回：
比较前两个数， 4比5小，交换位置 5 4 6 1 2 3
比较第2第3个数， 4比6小，交换位置 5 6 4 1 2 3
比较第3第4个数， 4比1大，位置不变 5 6 4 1 2 3
比较第4第5个数， 1比2小，交换位置 5 6 4 2 1 3
比较最后两个数， 1比3小，交换位置 5 6 4 2 3 1
第一回结束
第二回重复第一趟过程得到 6 5 4 3 2 1
排序完毕。
第二回排序结束后，所有数据已经排好序了。实际上，我们在对于一组数据进行冒泡排序时，假如需要排列的数据个数为 n 个，那么 n-1 趟一定能排好序，比如因为第 2 趟都会有前 2 个小的数排序好，n-1 趟前 n-1 小的数已排好序，最后一个数自然也排好序了。
代码实现：
import java.util.Scanner;
import java.util.Stack;
public class Main {
static void BubbleSort(int arr[])
{
int n=arr.length;
for(int i = 0; i < n - 1; i++)
{
for(int j = 0; j < n - i - 1; j++)
{
if(arr[j] > arr[j+1]){
int temp= arr[j+1];
arr[j+1]=arr[j];
arr[j]=temp;
}
}
}
}
public static void main(String[] args)
{
int a[] =new int []{4, 5, 6, 1, 2, 3};
BubbleSort(a);
for(Object c:a)
System.out.print(c+" ");
}
}
桶排序
（一般用于判断出现了多少次）
- 基本思想
桶排序的思想是，若待排序的记录的关键字在一个明显有限范围内时，可设计有限个有序桶，每个桶只能装与之对应的值，顺序输出各桶的值，将得到有序的序列。简单来说，在我们可以确定需要排列的数组的范围时，可以生成该数值范围内有限个桶去对应数组中的数，然后我们将扫描的数值放入匹配的桶里的行为，可以看作是分类，在分类完成后，我们需要依次按照桶的顺序输出桶内存放的数值，这样就完成了桶排序。
例如，要求我们输入 n 个 0~9 之间的整数，由小到大排序输出，我们可以准备 10 个桶依次编号为 0~9。那么，输入的数 0 则入 0 号桶，1 入 1 号桶，依次类推。
如图所示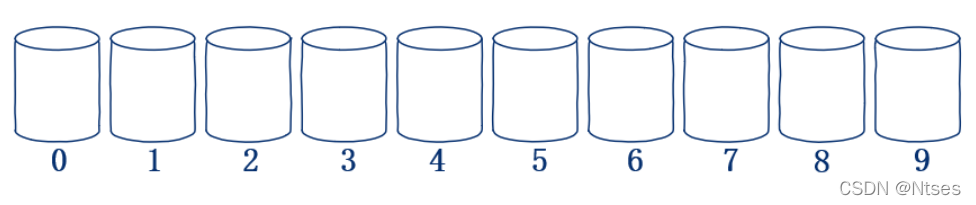
如上图所示 ，我们已准备好 10 个空桶并编号。
下面我们依次输入 8 个整数，分别是 2，5，6，8，5，2，9，6，我们每输入一个数值就将其放入对应的桶。
输入完毕后桶内数据如图所示：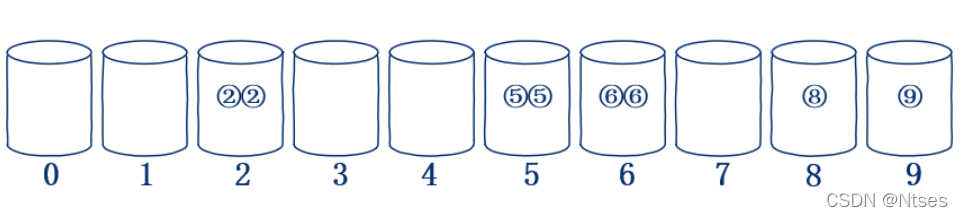
- 桶排序过程：
- 如上图所示，2 号桶内有两个数字 2，5 号桶内有两个数字 5，6 号桶内有两个数字 6，8 号桶内有一个数字 8，9 号桶内有一个数字 9
- 然后我们按桶编号从小到大的顺序将桶内数字输出，得到 2，2，5，5，6，6，8，9，至此桶排序完成。
注意：桶排序需要注意适用范围，在已知所需排序数据的范围下可以使用
代码实现：
int a[]=new int[10];
int n;
Scanner in =new Scanner(System.in)
n=in.nextInt();
for(int i=0;i<n;i++){
int key;
key=in.nextInt();
a[key]++;
}
for(int i=0;i<a.length;i++){
for(int j=0;j<a[i];j++){
System.out.print(i+" ");
}
}
插入排序
- 基本思想
插入排序是一种简单的排序方法，时间复杂度为 O(n*n)，适用于数据已经排好序，插入一个新数据的情况。其算法的基本思想是，假设待排序的数据存放在数组 a[1...n] 中，增加一个节点 x 用于保存当前数据，进行比较，a[1]即作为有序区，a[2...n] 作为无序区。
- 从 i=2 起直至 i=n 为止，通过循环遍历，将 a[i] 放在恰当的位置，使 a[1...i] 数据序列有序
我们现在有一个数组 a=[3 2 4 1 6 5 2 7]，需要使用插入排序进行排列。
第0步：[3] 2 4 1 6 5 2 7
第1步：[2 3] 4 1 6 5 2 7
第2步：[2 3 4] 1 6 5 2 7
第3步：[1 2 3 4] 6 5 2 7
第4步：[1 2 3 4 6] 5 2 7
第5步：[1 2 3 4 5 6] 2 7
第6步：[1 2 2 3 4 5 6] 7
第7步：[1 2 2 3 4 5 6 7]
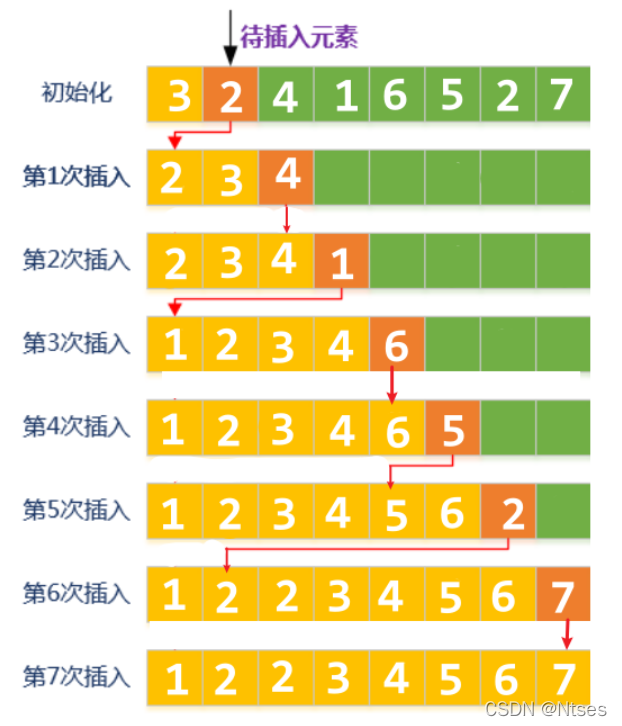
代码实现：
import java.util.Scanner;
import java.util.Stack;
public class Main {
static void insert_Sort(int[] a)
{
int len;
len = a.length;
for (int i=0; i<len; i++)
{
int x = a[i];
int j = i - 1;
while( j>=0&&x < a[j] )
{
a[j + 1] = a[j];
j -= 1;
}
a[j + 1] = x;
}
}
public static void main(String[] args)
{
int a[] =new int []{0, 3, 2, 4, 1, 6, 5, 2, 7};
insert_Sort(a);
for(Object c:a)
System.out.print(c+" ");
}
}
高效排序算法
前面，介绍了简单的排序算法，但在实际应用中，简单的排序算法很难达到效率的要求，所以再介绍了两种高效的排序算法，使排序时间复杂度大大减少。
快速排序
- 基本思想
快速排序是一种采用分治法解决问题的一个典型应用，也是冒泡排序的一种改进。它的基本思想是，通过一轮排序将待排记录分割成独立的两部分，其中一部分均比另一部分小，则可分别对这两部分继续进行排序，已达到整个序列有序。排序的时间复杂度为 O(nlogn)，相比于简单排序算法，运算效率大大提高。
- 算法步骤
- 从序列中取出一个数作为中轴数；
- 将比这个数大的数放到它的右边，小于或等于他的数放到它的左边；
- 再对左右区间重复第二步，直到各区间只有一个数。
例如，对这10 个数（6 1 2 7 9 3 4 5 10 8）进行快速排序：
以第一个数为基准数，在初始状态下，数字 6 在序列的第 1 位，我们的目标是将 6 挪到序列中间的某个位置，假设这个位置是 k 。
现在就需要寻找这个 k ，并且以第 k 位为分界点，左边的数都≤6，右边的数都≥6。那么如何找到这个位置 k 呢？
我们要知道，快速排序其实是冒泡排序的一种改进，冒泡排序每次对相邻的两个数进行比较，这显然是一种比较浪费时间的。
而快速排序是分别从两端开始”探测”的，先从右往左找一个小于 6 的数，再从左往右找一个大于 6 的数，然后交换他们。这里可以用两个变量 i 和 j ，分别指向序列最左边和最右边。
1.我们首先让 i 指向序列的最左边，指向数字 6；让 j 指向序列的最右边，指向数字 8，
2. j 一步一步地向左挪动，直到找到一个小于 6 的数停下来； i 再一步一步向右挪动，直到找到一个数大于 6 的数停下来
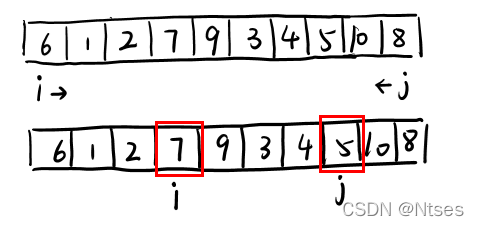
3.交换i、j的值
到此，第一次交换结束。接下来开始 j 继续向左挪动（再友情提醒，每次必须是 j 先出发）。发现了 4<6，停下来。 i 也继续向右挪动的，发现了 9>6，停下来。此时再次进行交换，交换之后的序列如下
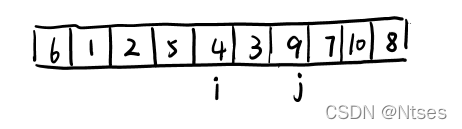
第二次交换结束。 j 继续向左挪动，发现了 3<6，又停下来。 i 继续向右移动，此时 i 和 j 相遇了，i 和 j 都移动到 3 面前。
说明此时“探测”结束。我们将基准数 6 和 3 进行交换。交换之后的序列为：3 1 2 5 4 6 9 7 10 8
到此第一轮“探测”真正结束。
现在基准数 6 已经归位，此时以基准数 6 为分界点，6 左边的数都小于等于 6，6 右边的数都大于等于 6。
现在我们将第一轮“探测”结束后的序列，以 6 为分界点拆分成两个序列，左边的序列是“3 1 2 5 4”，右边的序列是“9 7 10 8”。接下来还需要分别处理这两个序列，因为 6 左边和右边的序列目前都还是混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理 6 左边和右边的序列即可。
实际上快速排序的每一轮处理其实就是将这一轮的基准数归为，直到所有的数都归为为止，排序就结束了。
实现代码：
public class qSort {
public static void qSort(int[] arr,int low,int high){
int i,j,temp,t;
if(low>=high){//当它俩指向同一个元素时表示探测停止
return;
}
i=low;
j=high;
//temp就是基准位
temp = arr[low];
while (i<j) {
//先看右边，依次往左递减
while (temp<=arr[j]&&i<j) {
j--;
}
//再看左边，依次往右递增
while (temp>=arr[i]&&i<j) {
i++;
}
//如果满足条件则交换
if (i<j) {
t = arr[j];
arr[j] = arr[i];
arr[i] = t;
}
}
//最后将基准为与i和j相等位置的数字交换
arr[low] = arr[i];
arr[i] = temp;
//递归调用左半数组
quickSort(arr, low, j-1);
//递归调用右半数组
quickSort(arr, j+1, high);
}
public static void main(String[] args){
int[] arr = new int [1000];
int n;
Scanner in=new Scanner(System.in);
n=in.nextInt();
for(int i=0;i<n;i++)
{
arr[i]=in.nextInt();
}
quickSort(arr, 0, n-1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
归并排序
- 基本思想
归并排序是由递归实现的，主要是分而治之的思想，也就是通过将问题分解成多个容易求解的局部性小问题来解开原本的问题的技巧。
归并排序在合并两个已排序数组时，如果遇到了相同的元素，只要保证前半部分数组优先于后半部分数组， 相同元素的顺序就不会颠倒。所以归并排序属于稳定的排序算法。
每次分别排左半边和右半边，不断递归调用自己，直到只有一个元素递归结束，开始回溯，调用 merge 函数，合并两个有序序列，再合并的时候每次给末尾追上一个最大 int 这样就不怕最后一位的数字不会被排序。
- 排序过程
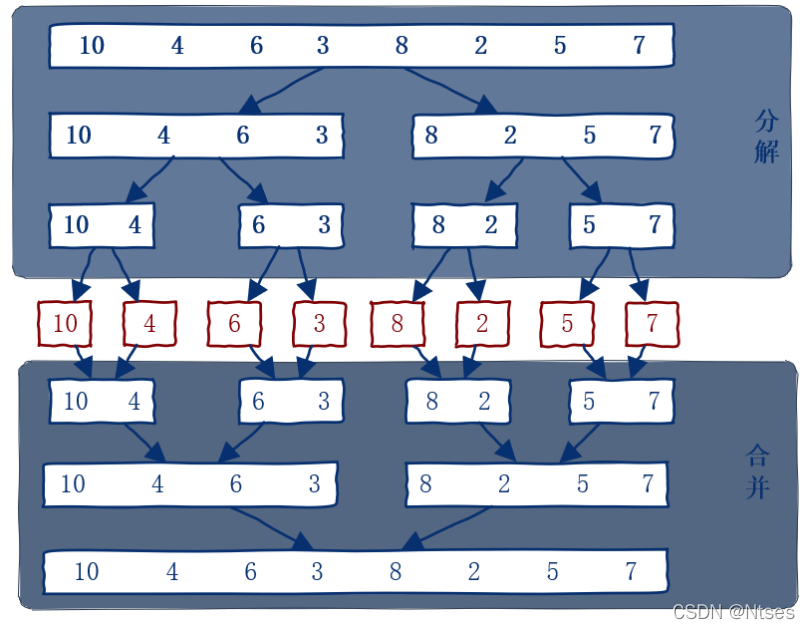
代码实现：
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
//分解
if(low<high){//分解到不能再分解的时候（每个板块里只有一个元素low=high）跳出该循环
sort(a,low,mid);
sort(a,mid+1,high);
//左右归并
merge(a,low,mid,high);
}
return a;
}
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high-low+1];
int i= low;
int j = mid+1;
int k=0;
// 把较小的数先移到新数组中
while(i<=mid && j<=high){
if(a[i]<a[j]){
temp[k++] = a[i++];
}else{
temp[k++] = a[j++];
}
}
// 把左边剩余的数移入数组
while(i<=mid){
temp[k++] = a[i++];
}
// 把右边边剩余的数移入数组
while(j<=high){
temp[k++] = a[j++];
}
// 把新数组中的数覆盖原数组
for(int x=0;x<temp.length;x++){
a[x+low] = temp[x];
}
}
public static void main(String[] args){
int[] arr = new int [1000];
int n;
Scanner in=new Scanner(System.in);
n=in.nextInt();
for(int i=0;i<n;i++)
{
arr[i]=in.nextInt();
}
sort(arr, 0, n-1);
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}
}
希尔排序
- 基本思想
希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法，同时也突破了之前内排序算法复杂度为 O(n2)的限制。
希尔排序是基于插入排序的以下两点性质而提出改进方法的：
- 插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率.
- 插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位
该方法的基本思想是：
先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。
因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率上比前两种方法有较大提高。
其中增量序列的选择是非常关键的，但通常我们取步长为 n/2（数组长度的一般）然后一直取半直到 1。
代码实现：
public class Shell
{
public static int[] sort(int[] arr,int n){
int gap = n/2;
while(gap > 0){
for(int j = gap; j < n; j++){
int i=j;
while(i >= gap && arr[i-gap] > arr[i]){
int temp = arr[i-gap]+arr[i];
arr[i-gap] = temp-arr[i-gap];
arr[i] = temp-arr[i-gap];
i -= gap;
}
}
gap = gap/2;
}
return arr;
}
public static void main(String[] args)
{
int[] arr = new int [1000];
int n;
Scanner in=new Scanner(System.in);
n=in.nextInt();
for(int i=0;i<n;i++)
{
arr[i]=in.nextInt();
}
int[] ans = sort(arr,n);
for(int a: ans){
System.out.println(a);
}
}
}
在我们日常使用的编译语言中，都是预先设置好排序算法的，只需要直接调用即可。但是有些情况是不能调用排序算法的，比如特殊的结构体排序而且要求是稳定的这种情况，所以需要我们在上面各种排序算法的原理的基础上进行改写。大部分情况下我们都是可以直接调用的。
排序初步
对一组无序的整数用排序算法进行排序，方法不限。
输入要求
第一行为数列的总个数，第二行为待排序的数列
输出要求
排序后的数列
样例输入
8
10 4 6 3 8 2 5 7
样例输出
2 3 4 5 6 7 8 10
Java 的 sort 是在 Arrays 里面定义的，用的时候可以缺省也可以自定排序比方式，只需要继承 Comparator 改写即可。
代码如下：
import java.util.Arrays;
import java.util.Comparator;
public class Main {
class MyComparator implements Comparator<Integer> {
@Override
public int compare(Integer a, Integer b) {
return a > b ? -1 : 1;
}
}
public static void main(String[] args) {
int[] arr = new int [1000];
int n;
Scanner in=new Scanner(System.in);
n=in.nextInt();
for(int i=0;i<n;i++)
{
arr[i]=in.nextInt();
}
Comparator cmp = new MyComparator();
Arrays.sort(arr, cmp); //也可以缺省cmp
for (int x : arr) {
System.out.print(x + " ");
}
}
}
扫一扫
469
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
