Save Energy!

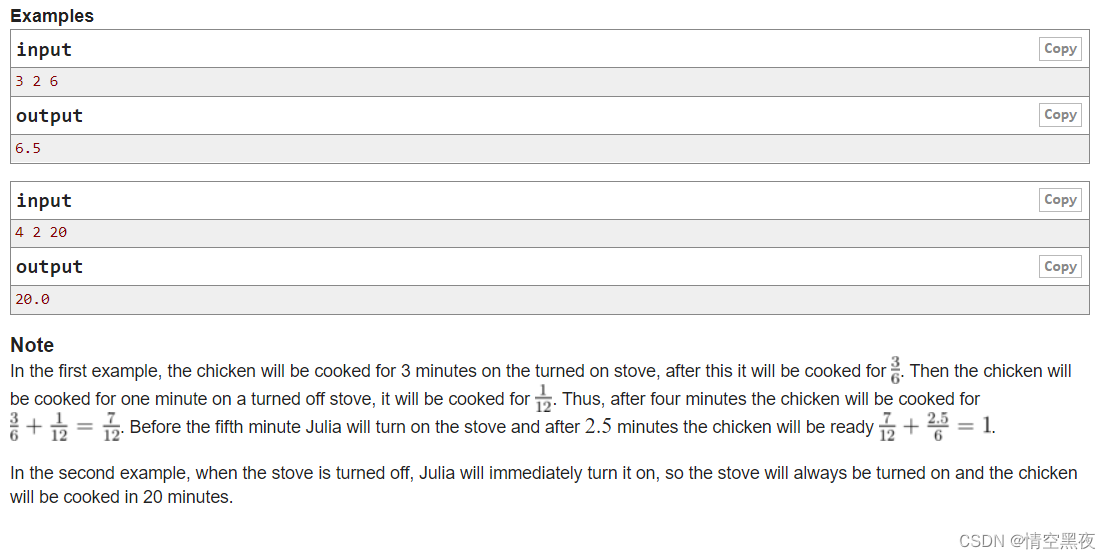
题意：

要烤一只鸡 ，烤鸡的时间的是t, 当炉子开火时，需要t分钟，当炉子没火是需要2 * t分钟，k代表点一次火可以持续多少的时间，d代表每经过d分钟，那个人来一次看一下火，如果还在，就不动，如果不在，就点火（这里其实是有歧义的，题目说橱子每d分钟去厨房，去厨房是待在厨房，还是瞬间出来，这里是做完事瞬间出来） ，问要经过多少时间才能把鸡炖好。

思路：

一种思路是看k和d的大小，k == d或者k < d或者 k > d，讨论这三种情况，分类讨论，然后还要群计算每一个的区间和范围，让人的感觉就是量非常大，无从下手，以后遇到这种情况就要想，肯定有简单的方法，确实。考虑，不管k和d的大小关系如何，最后肯定是会从d又开始的，那这样就是一个周期了，如何求这个周期，k个最多可以覆盖几个d, round = ceil(k / d) * d, 这个就是周期，然后思考有几个这样的周期，考虑，一个周期可以对烤鸡贡献多少，k * (1 / t) + ( round - k) (1 / (2 * t)），总的量为1，有小数，但是我想要整数，那就放大，两边同乘2 * t, 得到 num = 2 * k + (round - k),这个就是当总的量为2 * t时的贡献，cnt = 2 * t / num, 这个就是完整的周期数，left = 2 * t - cnt * (2 * t / num * round), k分钟能够贡献2 * k那对于left, 如果 <= 2 * k，那么需要的时间就是lef*1.0 / 2, 如果需要的时间 > 2 * k, 那么需要的时间就是k + (left - 2 * k)

#include <bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(false);
using namespace std;
 
typedef long long ll;
 
ll k, d, t;
 
int main()
{
	//IOS; cin.tie(0), cout.tie(0);
	cin >> k >> d >> t;
	ll round = ceil((double)k / d) * d;	//周期时间 
	ll num = 2 * k + (round - k);	//一个周期的贡献 
	ll cnt = 2 * t / num;	//有几个周期 
	ll left = 2 * t - cnt * num;	//剩下的时间 
	double ans = 0;
	if (left <= 2 * k)
	{
		ans = cnt * round + left * 1.0 / 2.0; 
	}
	else
	{
		ans = cnt * round + k + (left - 2 * k);
	}
	
	printf("%.10f\n", ans);
	return 0;
}