山东大学计算机学院机器学习实验二

最新推荐文章于 2025-10-28 21:12:19 发布

原创

最新推荐文章于 2025-10-28 21:12:19 发布 · 1.1k 阅读

24 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #人工智能

山东大学计算机学院机器学习实验二（Python Version）

实验目的：
本实验的目的是使用牛顿法针对二元分类问题实现逻辑回归。目标是建立一个模型，可以根据学生两次考试的成绩来估计大学录取机会。该实验包括绘制数据、应用牛顿法最小化目标函数以及分析结果。
实验步骤：
数据：实验使用的数据集代表 40 名被大学录取的学生和 40 名未录取的学生。每个训练
请添加图片描述
示例都包含学生在两次标准化考试中的分数以及指示录取或未录取的标签。
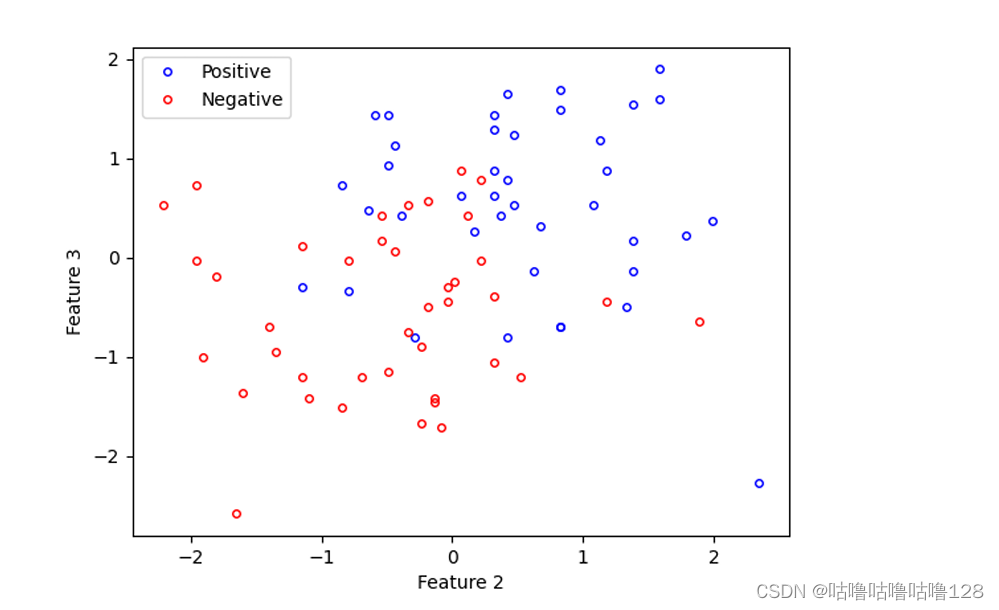
绘制数据：在应用牛顿法之前，使用不同的符号绘制数据来表示两个类别（录取和未录取）。

绘制出的图像如图所示：

**逻辑回归：**逻辑回归的假设函数定义为 hθ(x) = g(θTx)，其中 g 是 sigmoid 函数。
定义似然函数J(θ)和对数似然函数L(θ)以方便计算。目标是最小化负对数似然函数
L(θ)。
损失函数和梯度更新函数的定义如下：
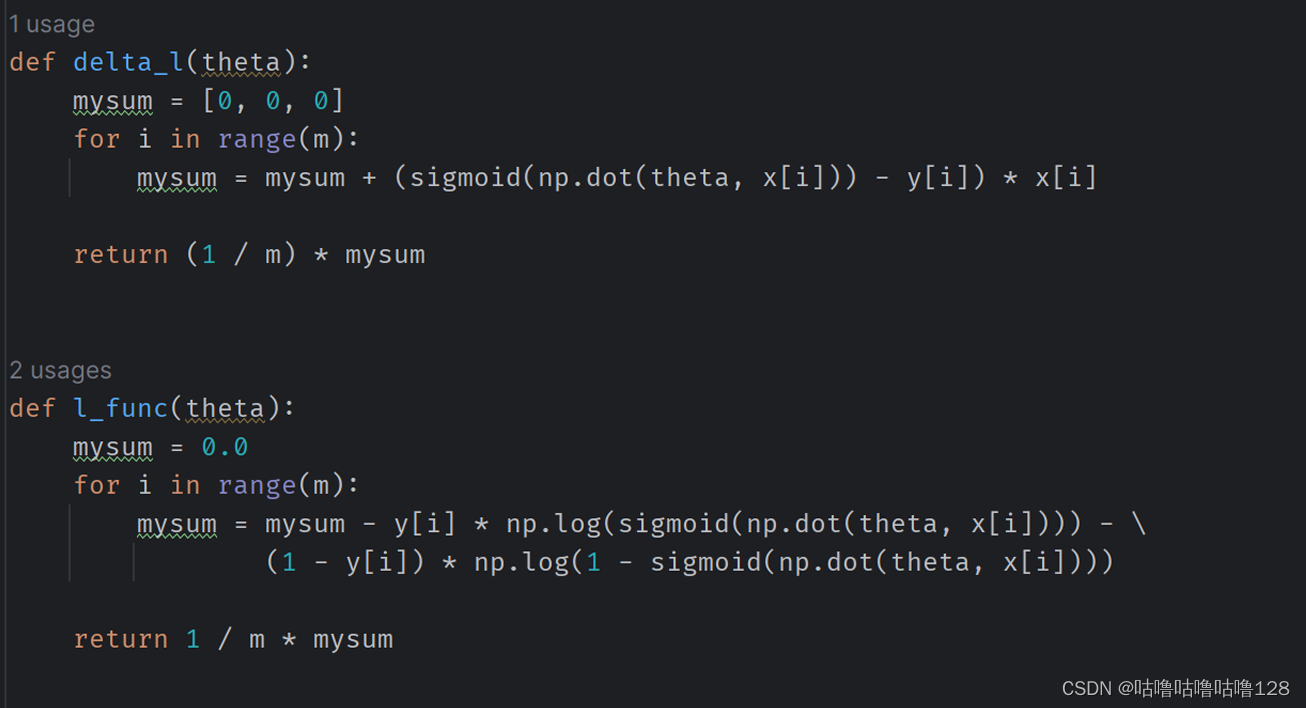
请添加图片描述

梯度下降法：最小化目标函数的一种方法是梯度下降。该算法迭代更新 θ，直到连续迭代中目标函数值之间的差异小于阈值 ϵ。计算达到收敛所需的迭代次数、收敛后的θ值以及迭代中L(θ)的减少量。
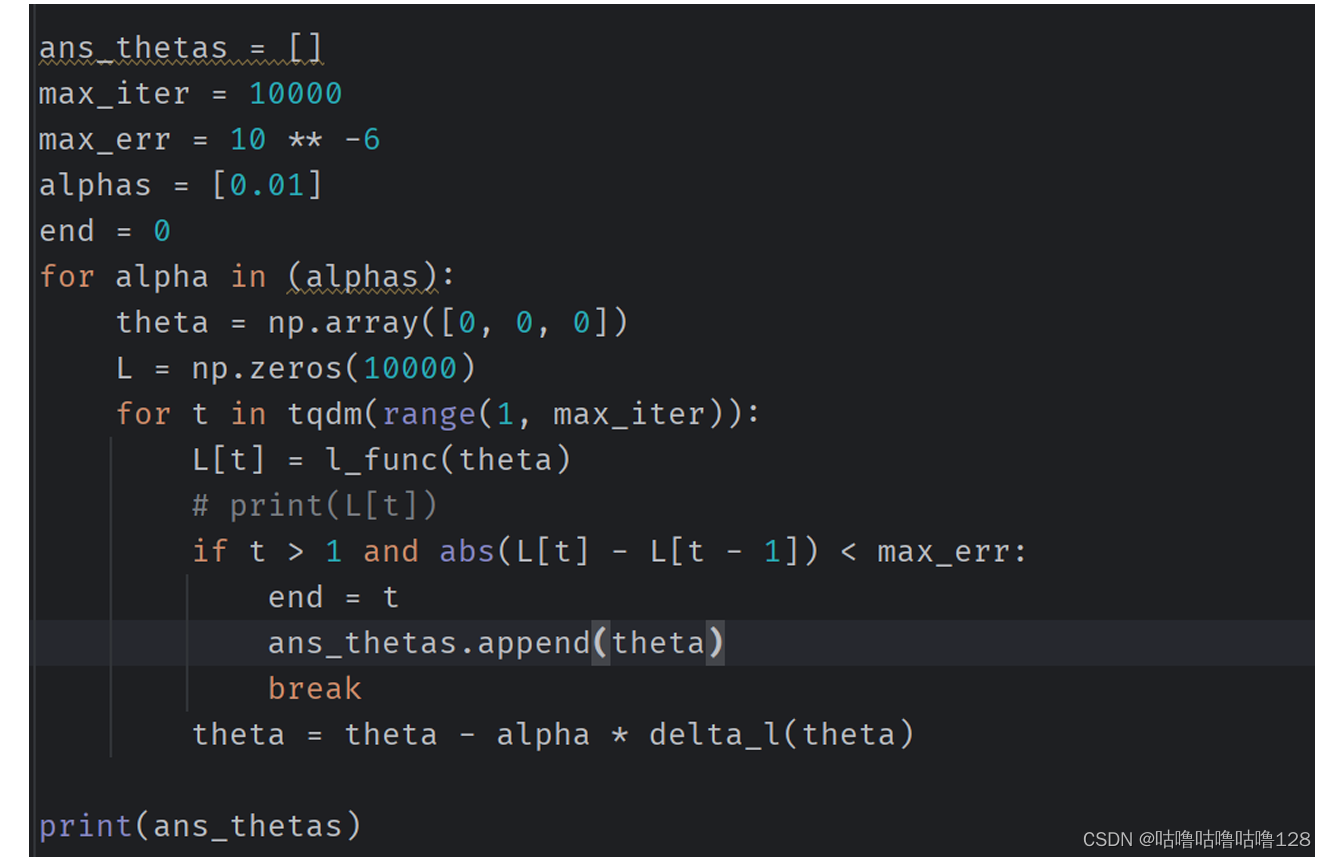
请添加图片描述

梯度下降法决策边界：收敛后，θ 的值用于查找分类问题中的决策边界。决策边界定义
为 P(y=1|x;θ) = g(θTx) = 0.5 的线，对应于 θTx = 0。绘制决策边界。
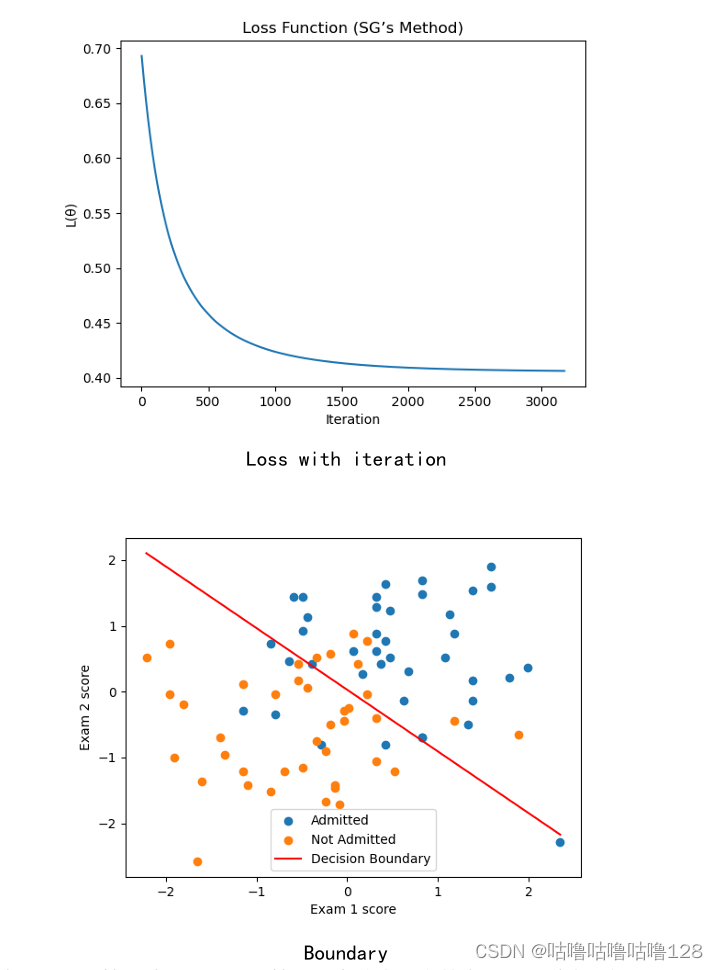
请添加图片描述
梯度下降法概率计算：使用 θ 值计算两次考试中具有特定分数的学生不被录取的概率。

Final概率：0.6538676322127192
牛顿法：求导数：计算损失函数对参数的一阶导数（梯度）和二阶导数（Hessian矩阵）

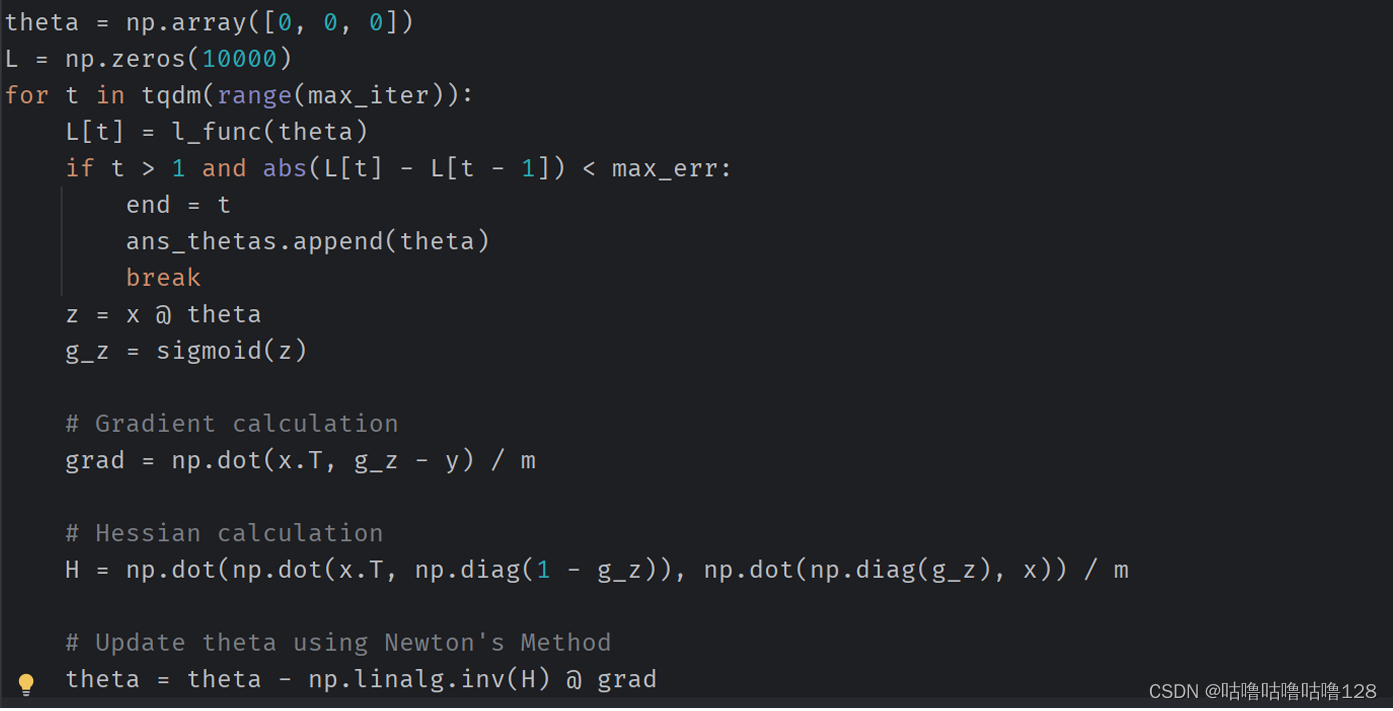
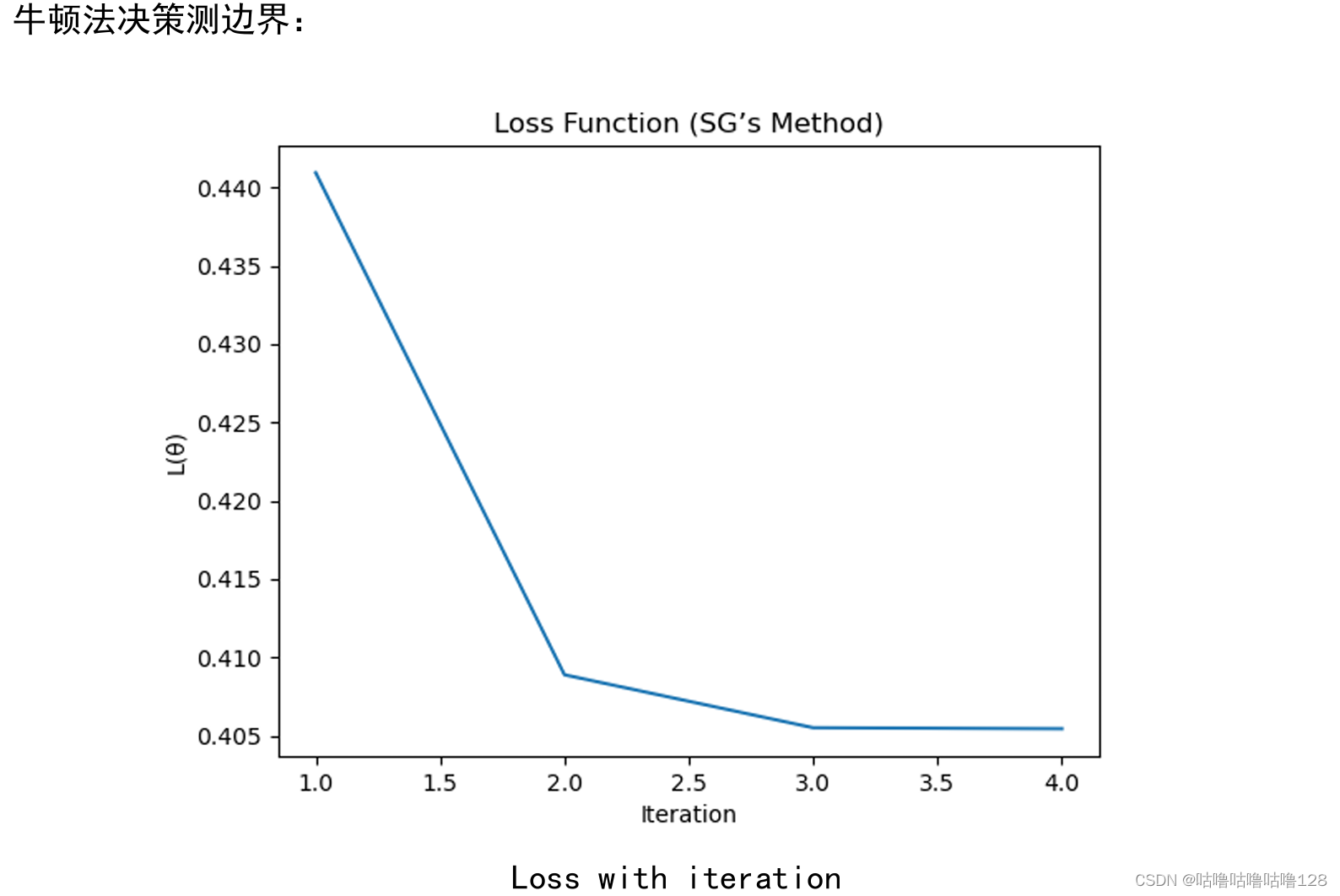
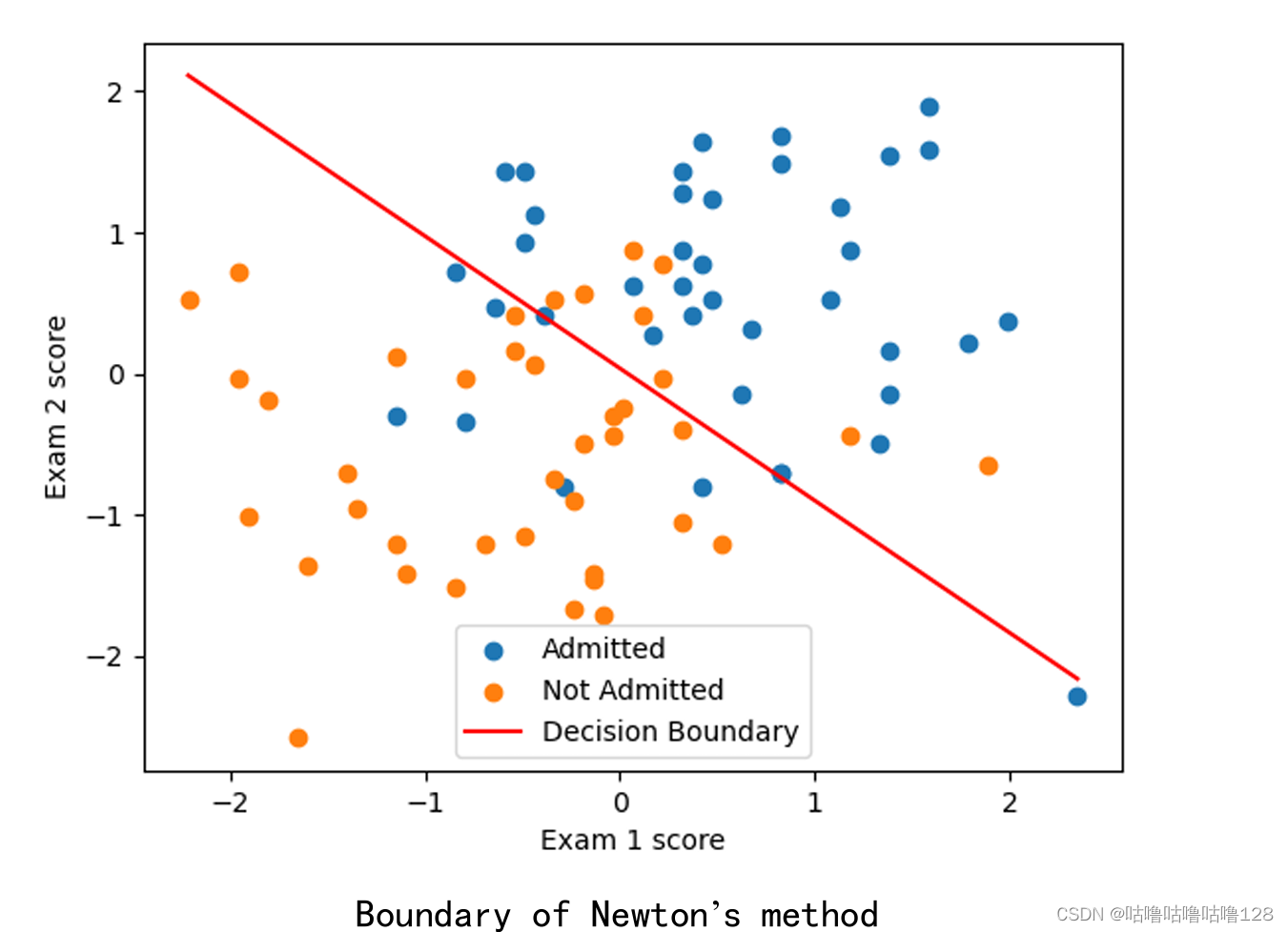
Newton’s method概率计算：使用 θ 值计算两次考试中具有特定分数的学生不被录取的概率。
请添加图片描述
Final 概率：0.6680218036811543
结论分析与体会：
实验的目的很清晰，就是用牛顿法解决一个二元分类问题，具体来说，就是通过学生两次考试的成绩来预测他们被大学录取的机会。
首先，我在实验报告中详细描述了实验目的，然后进入了实验步骤。我用不同的符号绘制数据，以区分录取和未录取的学生。逻辑回归的部分，我定义了假设函数、似然函数和对数似然函数，还介绍了梯度下降法作为最小化目标函数的一种方法。
我很自豪我的图形展示，特别是损失函数随迭代次数的变化和决策边界的绘制。这些图形直观地展示了算法的收敛过程和最终结果。
在牛顿法的部分，我展示了损失函数一阶导数和二阶导数的计算，以及相应的决策边界和概率计算。这个部分对我来说是个挑战，但我觉得我理解得还不错。
最后，我的结论部分总结了两种方法的最终概率，并对整个实验进行了分析。如果我能再多讨论一下两种方法的优劣势以及它们在实际问题中的应用，可能会更好。
总的来说，这是一个充实而有趣的实验，我觉得我对机器学习和数学方法有了更深的理解。
希望我的实验报告能为我的学习带来一些收获，也希望在未来的学习中能够继续进步！

# numpy实现
import numpy as np
from tqdm import tqdm
import matplotlib.pyplot as plt

# 指定.dat文件的路径
file_path1 = 'data2/ex2x.dat'

# 使用numpy的loadtxt函数读取数据
x = np.loadtxt(file_path1)
x = np.c_[np.ones(x.shape[0]), x]
x_ = x
# 计算均值和标准差
mean_x = np.mean(x, axis=0)
std_x = np.std(x, axis=0)
# 标准化数据
x[:, 1:] = (x[:, 1:] - mean_x[1:]) / std_x[1:]

# 指定.dat文件的路径
file_path = 'data2/ex2y.dat'

# 使用numpy的loadtxt函数读取数据
y = np.loadtxt(file_path)

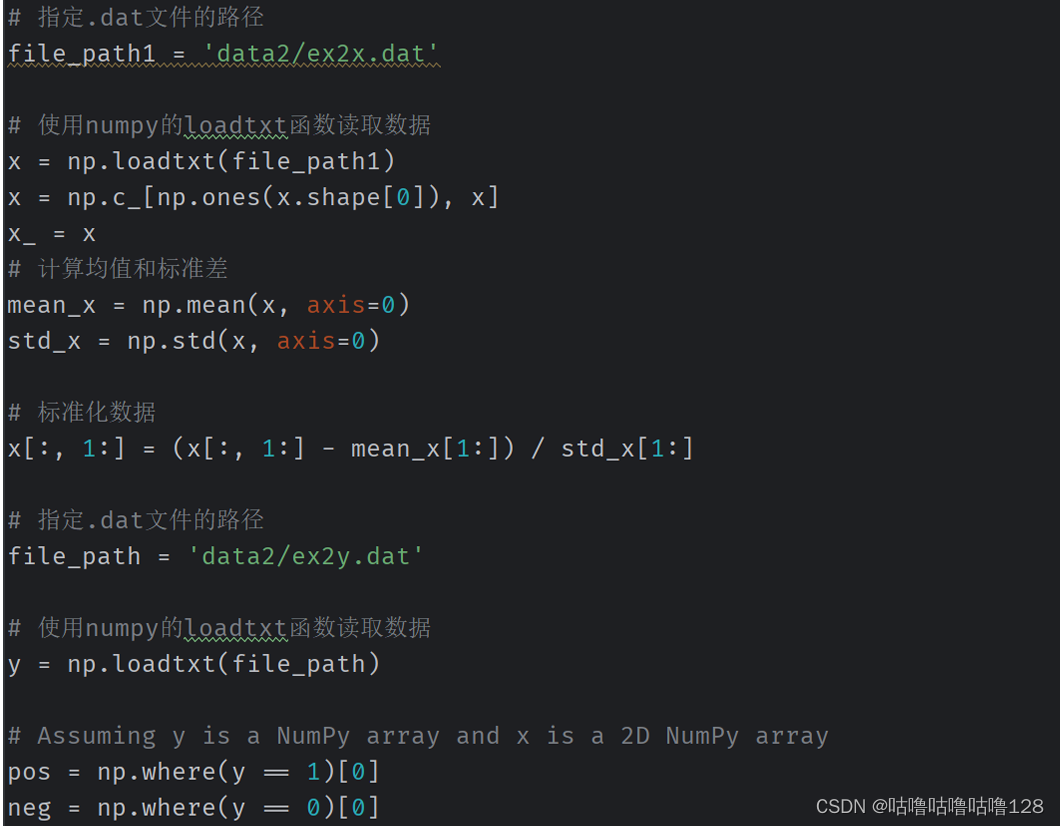
# Assuming y is a NumPy array and x is a 2D NumPy array
pos = np.where(y == 1)[0]
neg = np.where(y == 0)[0]

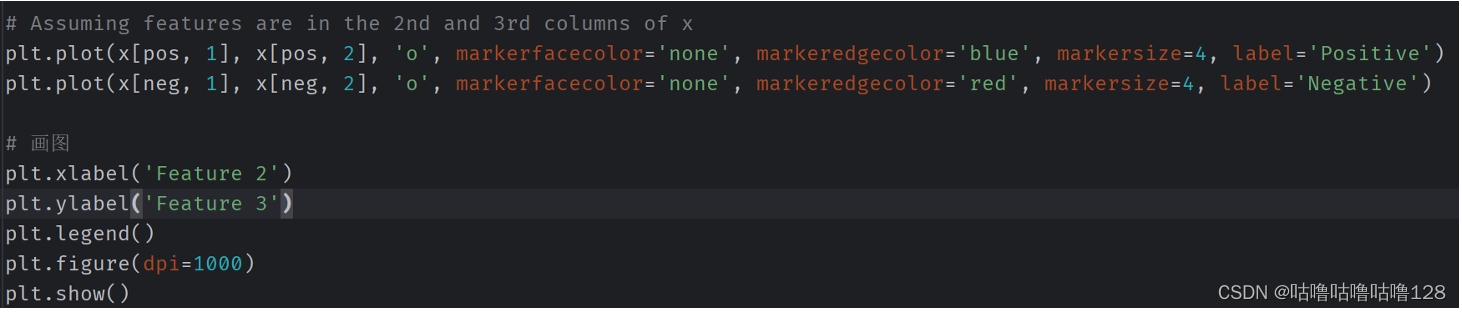
# Assuming features are in the 2nd and 3rd columns of x
plt.plot(x[pos, 1], x[pos, 2], 'o', markerfacecolor='none', markeredgecolor='blue', markersize=4, label='Positive')
plt.plot