中缀表表达式转后缀表达式

        在我们编程中，后缀表达式适合计算机进行运算，但是人却不容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将中缀表达式转为后缀表达式。

具体步骤

1.初始化两个栈：运算符栈s1和储存中间结果的栈s2

2.从左到右扫描中缀表达式

3.遇到数时压入s2

4.遇到运算符时，比较其与s1栈顶运算符的优先级；

        （1）如果s1为空，或栈顶运算符为左括号（，则直接将此运算符入栈

        （2 ）否则，若优先级比栈顶的运算符高，也将运算符压入s1

        （3）否则，将s1栈顶的运算符弹出并压入s2中，再次转到（4-1）与s1中新的栈顶运算符相比较；

5. 遇到括号时：

        （1）如果是左括号（，则直接压入s1，

        （2）如果是右括号），则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，

此时将这一对括号丢弃。

6.重复步骤2至5，直到表达式的最右边

7.将s1中剩下的运算符依次弹出并压入s2

8.依次弹出s2中的元素并输出，结果的逆序既为中缀表达式对应的后缀表达式

图解：

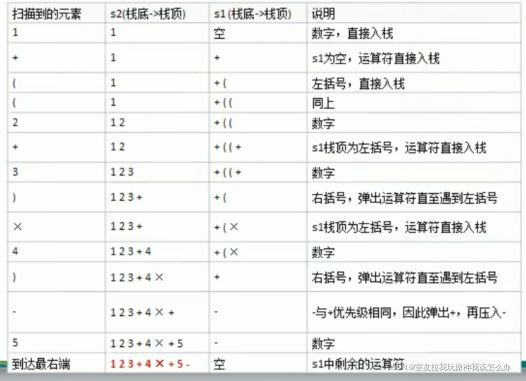
 代码实现

因为直接对String操作不方便，因此先将表达式转为对应的List

  /**
     * 方法：将中缀表达式转为对应的List
     *
     * @param s
     * @return
     */
    public static List<String> toInfixExpressionList(String s) {
        //定义一个List，存放中缀表达式对应的内容
        List<String> ls = new ArrayList<>();
        int index = 0;//定义一个指针，用来遍历中缀表达式字符串
        String str;//定义一个字符串来完成多位数的拼接
        char c;//每遍历出一位都放在c中
        do {
            //如果c是一个非数字，就直接放入list
            if ((c = s.charAt(index)) < 48 || (c = s.charAt(index)) > 57) {
                ls.add(c + "");//直接放入
                index++;//记住后移一位
            } else {//如果是一个数字就需要考虑多位数
                str = "";//初始化str
                while (index < s.length() && (c = s.charAt(index)) >= 48 && (c = s.charAt(index)) <= 57) {
                    str += c;//拼接
                    index++;//后移一位
                }
                //完成拼接后再放入list
                ls.add(str);
            }
        } while (index < s.length());//遍历到字符串最后一位
        return ls;//将list返回
    }

 效果展示

  String expression = "1+((2+3)*4)-5";
        List<String> list = toInfixExpressionList(expression);
        System.out.println(list);

[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]

 在将String转为list后我们还需要写一个方法就是定义各个运算符的优先级

/**
 * 类：编写一个Operation类 可以返回一个运算符，对应的优先级
 */
class Operation {
    private static int ADD = 1;//加
    private static int SUB = 1;//减
    private static int MUL = 2;//乘
    private static int DIV = 2;//除

    /**
     * 方法：返回对应优先级的数字
     */
    public static int getValue(String operation) {
        int result = 0;
        switch (operation) {
            case "+":
                result = ADD;
                break;
            case "-":
                result = SUB;
                break;
            case "*":
                result = MUL;
                break;
            case "/":
                result = DIV;
                break;
            default:
                break;
        }
        return result;
    }
}

那么我们就正式开始写中缀表达式转后缀表达式的方法 

/**
     * 方法：将得到的中缀表达式对应的list转换为后缀表达式对应的list
     *
     * @param ls
     * @return
     */
    public static List<String> parseSuffixExpressionList(List<String> ls) {
        //定义两个栈
        Stack<String> s1 = new Stack<String>();//符号栈
        //注：因为s2这个栈，在整个程序中都没有出栈的操作，而后面我们还需要对表达式逆序
        //因此比较麻烦，还不如使用List<String>
        //Stack<String> s2 = new Stack<String>();
        List<String> s2 = new ArrayList<String>();//储存中间结果的List s2

        //遍历
        for (String item : ls) {
            //如果是一个数则直接加入s2
            if (item.matches("\\d+")) {//正则匹配数字
                s2.add(item);
            } else if (item.equals("(")) {//如果是左括号（就直接入s1栈
                s1.push(item);
            } else if (item.equals(")")) {
                //如果是右括号），则依次弹出s1栈顶的运算符，并压入s2，直到遇到左括号为止，
                while (!s1.peek().equals("(")) {
                    s2.add(s1.pop());
                }
                s1.pop();//遍历到左括号再将左括号丢弃
            } else {
                //若time优先级小于等于s1栈顶运算符，将s1栈顶的运算符弹出并加入s2中，并再次与s1中的新栈顶运算符作比较
                //比较优先级的方法使用Operation中的静态方法getValue（）
                while (s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item)) {
                    s2.add(s1.pop());
                }
                //还需要将itme压入s1栈中
                s1.push(item);
            }
        }
        //将s1中剩余的运算符依次加入s2中
        while (s1.size() != 0) {
            s2.add(s1.pop());
        }
        //将s2返回，因为是ArraysLise所以不需要逆序
        return s2;
    }

 效果展示

 String expression = "1+((2+3)*4)-5";
        List<String> list = toInfixExpressionList(expression);
        System.out.println("中缀表达式："+list);
        List<String> ExpressionList = parseSuffixExpressionList(list);
        System.out.println("后缀表达式："+ExpressionList);

 

中缀表达式：[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
后缀表达式：[1, 2, 3, +, 4, *, +, 5, -]

 我们在编写一个计算后缀表达式的方法

 /**
     * 完成对逆波兰表达式的运算
     */
    public static int calculate(List<String> ls) {
        //创建一个栈
        Stack<String> stack = new Stack<>();
        //遍历 ls
        for (String item : ls) {
            //使用正则表达式来取出数
            if (item.matches("\\d+")) {//匹配多位数
                //入栈
                stack.push(item);
            } else {
                //pop出两个数，并进行计算，再入栈
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if (item.equals("+")) {
                    res = num1 + num2;
                } else if (item.equals("-")) {
                    res = num1 - num2;
                } else if (item.equals("*")) {
                    res = num1 * num2;
                } else if (item.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("运算符错误");
                }
                //把res入栈
                stack.push(res + "");
            }
        }
        //将最后的结果返回
        return Integer.parseInt(stack.pop());
    }
}

 效果展示

 //将转为的后缀表达式放入计算机中
        int res = calculate(ExpressionList);
        System.out.println("计算的结果为：" + res);

中缀表达式：[1, +, (, (, 2, +, 3, ), *, 4, ), -, 5]
后缀表达式：[1, 2, 3, +, 4, *, +, 5, -]
计算的结果为：16