CVPR2016 | DeepFool | DeepFool：一种简单而准确的欺骗深度神经网络的方法

---

论文链接

本文 “DeepFool: a simple and accurate method to fool deep neural networks” 提出 DeepFool 算法，用于高效计算能欺骗深度神经网络的扰动，量化分类器的鲁棒性。实验表明，该算法在计算对抗扰动和提升分类器鲁棒性方面优于现有方法。

---

摘要-Abstract

State-of-the-art deep neural networks have achieved impressive results on many image classification tasks. However, these same architectures have been shown to be unstable to small, well sought, perturbations of the images. Despite the importance of this phenomenon, no effective methods have been proposed to accurately compute the robustness of state-of-the-art deep classifiers to such perturbations on large-scale datasets. In this paper, we fill this gap and propose the DeepFool algorithm to efficiently compute perturbations that fool deep networks, and thus reliably quantify the robustness of these classifiers. Extensive experimental results show that our approach outperforms recent methods in the task of computing adversarial perturbations and making classifiers more robust.

最先进的深度神经网络在许多图像分类任务上取得了令人瞩目的成果。然而，这些相同的架构已被证明对图像的微小、精心寻找的扰动不稳定。尽管这种现象很重要，但尚未提出有效的方法来准确计算最先进的深度分类器在大规模数据集上对此类扰动的鲁棒性。在本文中，我们填补了这一空白，并提出了 DeepFool 算法，以有效地计算能欺骗深度网络的扰动，从而可靠地量化这些分类器的鲁棒性。大量的实验结果表明，我们的方法在计算对抗性扰动和使分类器更具鲁棒性的任务中优于最近的方法。

---

引言-Introduction

这部分内容主要介绍了研究背景、研究目的和主要贡献，具体如下：

1. 研究背景：深度神经网络在生物信息学、语音和计算机视觉等众多领域的模式识别任务中取得了卓越的成果。然而，其对对抗扰动表现出不稳定性，即对数据样本进行微小且难以察觉的扰动，就足以使当前先进的分类器出现误分类。这种对抗扰动的存在似乎与学习算法的泛化能力相矛盾，且从安全角度来看，不同模型间的对抗扰动具有一定的通用性，值得关注。
2. 研究目的：精确计算对抗扰动的方法对于研究和比较不同分类器的鲁棒性至关重要，它有助于理解当前网络架构的局限性，以及设计提升鲁棒性的方法。但目前尚未有完善的方法来计算对抗扰动，本文旨在填补这一空白。
3. 主要贡献：提出一种简单且准确的方法，用于计算和比较不同分类器对对抗扰动的鲁棒性；通过大量实验对比，验证了该方法在计算对抗扰动时比现有方法更可靠、高效，且利用对抗样本扩充训练数据能显著提升分类器的鲁棒性；指出使用不精确的方法计算对抗扰动可能会得出误导性结论，本文方法能更好地理解这一现象及其影响因素。

图1：对抗扰动的示例。第一行：原始图像 $x$，其分类结果为 $\hat{k}(x)=“鲸鱼”$。第二行：图像 $x+r$，分类结果为 $\hat{k}(x+r)=“海龟”$，以及通过DeepFool算法计算得到的相应扰动 $r$. 第三行：分类为“海龟”的图像，以及通过快速梯度符号法计算得到的相应扰动。DeepFool算法得到的扰动更小。

---

针对二分类器的DeepFool-DeepFool for binary classifiers

该部分主要介绍了针对二分类器的DeepFool算法，先分析线性分类器情况得出闭式解，再通过迭代线性化处理一般可微分类器，具体内容如下：

1. 线性二分类器的对抗扰动求解：由于多分类器可看作多个二分类器的集合，所以先研究二分类器的情况。假设二分类器 $\hat{k}(x)=sign(f(x))$，当 $f(x)$ 是仿射分类器，即 $f(x)=w^{T}x+b$ 时，其在点 $x_0$ 处的鲁棒性 $\Delta (x_0;f{)}^2$ 等于 $x_0$ 到分离超平面 { x : w T x + b = 0 } \{x: w^{T} x + b = 0\} {x:wTx+b=0} 的距离。使分类器决策改变的最小扰动 $r_{\ast }(x_0)$，就是 $x_0$ 在该超平面上的正交投影，可由闭式公式 $r_{\ast }(x_0)=-\frac{f(x_0)}{\Vert w{\Vert }_2^2}w$ 得出。
   
   图2：线性二分类器的对抗样本。
2. 一般二分类器的DeepFool算法：当 $f(x)$ 是一般的二分类可微分类器时，采用迭代过程来估计鲁棒性 $\Delta (x_0;f)$。每次迭代时，在当前点 $x_i$ 处对 $f(x)$ 进行线性化，计算线性化后分类器的最小扰动 $r_i$，公式为 $\underset{r_i}{\mathrm{argmin}}{\Vert r_i\Vert }_{2}subjecttof(x_i)+\nabla f(x_i{)}^T{r}_i=0$，并根据 $r_i$ 更新下一个迭代点 $x_{i+1}$。算法在 $x_{i+1}$ 使分类器符号改变时停止。在实际应用中，为使最终扰动向量能到达分类边界另一侧，会将其乘以常数 $1+\eta$（实验中 $\eta =0.02$） 。该算法总结在算法1中，还给出了二维情况下的几何图示，帮助理解算法的迭代过程和原理。
   
   
   图3：$n=2$ 时算法1的示意图。假设 $x_0\in {\mathbb{R}}^n$. 绿色平面是函数 $x\mapsto f(x_0)+\nabla f(x_0{)}^T(x-x_0)$ 的图像，该函数与分类器函数（线框图形）$x\mapsto f(x)$ 相切。橙色线表示 $f(x_0)+\nabla f(x_0{)}^T(x-x_0)=0$ 的位置。$x_1$ 是通过将 $x_0$ 投影到 ${\mathbb{R}}^n$ 中的橙色超平面上从 $x_0$ 得到的。

---

多分类器的DeepFool算法-DeepFool for multiclass classifiers

这部分主要介绍了将DeepFool算法扩展到多分类器的情况，包括基于常见的一对多分类方案，分别对线性和一般多分类器的处理，以及算法在不同范数下的扩展，具体如下：

1. 一对多分类方案下的多分类器定义：多分类器常用一对多分类方案，此时分类器 $f:{\mathbb{R}}^n\to {\mathbb{R}}^c$（$c$ 为类别数），分类决策通过 $\hat{k}(x)=\underset{k}{\mathrm{argmax}}{f}_k(x)$ 进行，其中 $f_k(x)$ 是对应第 $k$ 类的输出。
2. 线性多分类器的对抗扰动计算
   • 问题转化：对于线性多分类器 $f(x)=W^{\top }x+b$，寻找最小扰动以欺骗分类器的问题可转化为计算样本 $x_0$ 到凸多面体 $P$ 补集的距离。 P = ⋂ k = 1 c { x : f k ^ ( x 0 ) ( x ) ≥ f k ( x ) } P=\bigcap_{k = 1}^{c}\{x: f_{\hat{k}(x_{0})}(x) \geq f_{k}(x)\} P=⋂k=1c​{x:fk^(x0​)​(x)≥fk​(x)}，该多面体定义了分类器输出标签为 $\hat{k}(x_0)$ 的区域。
   • 求解方法：定义 $\hat{l}(x_0)$ 为 $P$边界上离 $x_0$ 最近的超平面，通过公式 $\hat{l}(x_0)=\underset{k\ne \hat{k}(x_0)}{\mathrm{argmin}}\frac{\left|f_k(x_0)-f_{\hat{k}(x_0)}(x_0)\right|}{{\Vert w_k-w_{\hat{k}(x_0)}\Vert }_2}$ 计算。最小扰动 $r_{\ast }(x_0)$ 是 $x_0$ 在由 $\hat{l}(x_0)$ 索引的超平面上的投影，公式为 $r_{\ast }(x_0)=\frac{\left|f_{\hat{l}(x_0)}(x_0)-f_{\hat{k}(x_0)}(x_0)\right|}{{\Vert w_{\hat{l}(x_0)}-w_{\hat{k}(x_0)}\Vert }_2^2}(w_{\hat{l}(x_0)}-w_{\hat{k}(x_0)})$。算法通过迭代计算到达多面体 ${\bar{P}}_i$ 边界的扰动向量并更新当前估计值。
     
     图4：对于属于类别4的 $x_0$，设 F k = { x : f k ( x ) − f 4 ( x ) = 0 } \mathscr{F}_{k}=\{x: f_{k}(x) - f_{4}(x)=0\} Fk​={x:fk​(x)−f4​(x)=0}。这些超平面用实线表示，而 $P$ 的边界用绿色虚线表示。
     
     图5：对于属于类别4的 $x_0$，设 F k = { x : f k ( x ) − f 4 ( x ) = 0 } \mathscr{F}_{k}=\{x: f_{k}(x) - f_{4}(x)=0\} Fk​={x:fk​(x)−f4​(x)=0}。线性化后的零水平集用虚线表示，多面体 ${\tilde{P}}_0$ 的边界用绿色表示。
3. 一般多分类器的DeepFool算法：对于一般非线性多分类器，描述分类器输出 $\hat{k}(x_0)$ 区域的集合 $P$ 不再是多面体。借鉴二分类器的迭代线性化思路，在每次迭代 $i$ 时，用多面体 ${\tilde{P}}_i$ 近似 $P$，公式为 P ‾ i = ⋂ k = 1 c { x : f k ( x i ) − f k ^ ( x 0 ) ( x i ) + ∇ f k ( x i ) ⊤ x − ∇ f k ^ ( x 0 ) ( x i ) ⊤ x ≤ 0 } \overline{P}_{i}=\bigcap_{k = 1}^{c}\{x: f_{k}(x_{i}) - f_{\hat{k}(x_{0})}(x_{i})+\nabla f_{k}(x_{i})^{\top} x - \nabla f_{\hat{k}(x_{0})}(x_{i})^{\top} x \leq 0\} Pi​=⋂k=1c​{x:fk​(xi​)−fk^(x0​)​(xi​)+∇fk​(xi​)⊤x−∇fk^(x0​)​(xi​)⊤x≤0}. 该算法的优化策略与现有优化技术紧密相关，如在二分类情况下可视为牛顿迭代算法或自适应步长的梯度下降算法，多分类中的线性化类似于顺序凸规划。
   
4. 算法在 ${\ell }_p$ 范数下的扩展：本文虽主要使用 ${\ell }_2$ 范数衡量扰动，但算法框架可扩展到 ${\ell }_p$ 范数（$p\in [1,\infty )$）。只需对算法2中的更新步骤进行替换，当计算 ${\ell }_p$ 范数下的最小对抗扰动时，更新公式为 $\hat{l}\leftarrow \underset{k\ne k(x_0)}{\mathrm{argmin}}\frac{|f_k^{\prime }|}{{\Vert w_k^{\prime }\Vert }_q}$ 和 $r_i\leftarrow \frac{|f_i^{\prime }|}{{\Vert w_i^{\prime }\Vert }_q^q}{\left|w_i^{\prime }\right|}^{q-1}\odot sign\left(w_i^{\prime }\right)$（其中 $q=\frac{p}{p-1}$，$\odot$ 是逐元素乘积） 。特别地，当 $p=\infty$（即 ${\ell }_{\infty }$ 范数）时，更新步骤变为 $\hat{l}\leftarrow \underset{k\ne \hat{k}(x_0)}{\mathrm{argmin}}\frac{|f_k^{\prime }|}{{\Vert w_k^{\prime }\Vert }_1}$ 和 $r_i\leftarrow \frac{|f_{\hat{i}}^{\prime }|}{{\Vert w_{\hat{i}}^{\prime }\Vert }_1}sign\left(w_{\hat{i}}^{\prime }\right)$.

---

实验结果-Experimental Results

设置-Setup

该部分主要介绍了实验的数据集、模型、评估指标和对比方法，为后续实验结果的分析和比较奠定基础，具体内容如下：

1. 实验数据集与模型：在MNIST、CIFAR-10和ImageNet（ILSVRC 2012）这三个图像分类数据集上进行实验，选用多种深度神经网络架构。
   • MNIST数据集：使用一个两层全连接网络和一个两层LeNet卷积神经网络架构，都用带动量的随机梯度下降（SGD）算法，借助MatConvNet工具包进行训练。
   • CIFAR-10数据集：训练了一个三层LeNet架构以及一个Network In Network（NIN）架构。
   • ILSVRC 2012数据集：直接采用CaffeNet和GoogLeNet的预训练模型。
2. 评估指标：为评估分类器对对抗扰动的鲁棒性，使用平均鲁棒性 ${\hat{\rho }}_{adv}(f)$ 作为评估指标，计算公式为 ${\hat{\rho }}_{adv}(f)=\frac{1}{|\mathcal{D}|}{\sum }_{x\in \mathcal{D}}\frac{\Vert \hat{r}(x){\Vert }_2}{\Vert x{\Vert }_2}$。其中，$\hat{r}(x)$ 是通过DeepFool算法得到的估计最小扰动，$\mathcal{D}$ 代表测试集。该指标衡量了在测试集中，平均每个样本需要添加多大比例的扰动才能使分类器误判，数值越小，说明分类器对对抗扰动的鲁棒性越强。
3. 对比方法：将DeepFool算法与当前计算对抗扰动的先进技术进行对比，主要包括文献[18]和[4]中的方法。
   • 文献[18]方法-L-BFGS：通过求解一系列惩罚优化问题来寻找最小扰动。
   • 文献[4]方法-FGSM：即快速梯度符号法，通过 $\hat{r}(x)=ϵsign\left({\nabla }_{x}J(\theta ,x,y)\right)$ 来估计最小扰动。在实际操作中，由于没有通用规则确定参数 $ϵ$，所以选择能使90%的数据在扰动后被误分类的最小 $ϵ$ 值.

结果-Results

该部分呈现了DeepFool算法与其他方法在多个方面的对比实验结果，充分验证了DeepFool算法在计算对抗扰动和提升模型鲁棒性等方面的优势，具体内容如下：

1. 扰动大小与准确性对比：通过计算不同分类器在不同数据集上的平均鲁棒性，对比了DeepFool算法与文献[18]（L-BFGS）和[4]（FGSM）中方法生成的对抗扰动大小。结果显示，DeepFool估计的扰动明显小于竞争方法，更接近理论上的最小扰动。例如，在MNIST数据集上，LeNet网络使用DeepFool得到的平均扰动是快速梯度符号法（文献[4]方法）的五分之一；在ILSVRC2012挑战数据集上，DeepFool得到的平均扰动比快速梯度法小一个数量级，且比文献[18]的方法产生的扰动向量也略小，表明其能更精准地检测出可欺骗神经网络的方向。
2. 计算效率对比：DeepFool算法在计算效率上显著优于文献[18]的方法。文献[18]的方法需要对一系列目标函数进行代价高昂的最小化计算，而DeepFool算法通常在几次迭代（少于3次）内就能收敛到可欺骗分类器的扰动向量，在保证准确性的同时大幅提高了计算速度。
   
   表1：不同分类器在不同数据集上的对抗鲁棒性。各方法计算单个样本所需的时间列于“时间”栏中。这些时间是在一台不支持CUDA的2015年中期款MacBook Pro上计算得出的。带星号的值是使用GTX 750 Ti GPU计算得到的。
3. ${\ell }_{\infty }$范数下的对比结果：当使用 ${\ell }_{\infty }$ 范数衡量扰动时，DeepFool算法依然表现出色。实验数据表明，与其他计算对抗样本的方法相比，DeepFool生成的对抗扰动更小，更接近最优值，进一步证明了该算法的优越性。
   
   表2：基于DeepFool（最小 $l_{\infty }$ 扰动）和导致90%误分类的快速梯度符号法，四个不同网络的 ${\hat{\rho }}_{adv}^{\infty }$ 值。
4. 微调实验结果
   • 鲁棒性变化：使用DeepFool和快速梯度符号法生成的对抗样本对网络进行微调，以构建更鲁棒的分类器。结果显示，用DeepFool对抗样本微调能显著提升网络对对抗扰动的鲁棒性，如MNIST网络的鲁棒性提升了50%，NIN在CIFAR - 10上的鲁棒性提升约40%；而快速梯度符号法的对抗样本微调却可能降低网络鲁棒性。研究认为这是因为该方法估计的扰动远大于最小对抗扰动，使用过度扰动的图像微调网络会降低其鲁棒性，通过放大DeepFool对抗扰动范数的微调实验验证了这一假设。
     
     图6：
     （a）在MNIST数据集上，用两种不同方法计算的对抗样本对LeNet进行微调的效果。
     （b） 在MNIST数据集上，用两种不同方法计算的对抗样本对全连接网络进行微调的效果。
     （c） 在CIFAR-10数据集上，用两种不同方法计算的对抗样本对Network in Network（NIN）模型进行微调的效果。
     （d）在CIFAR-10数据集上，用两种不同方法计算的对抗样本对LeNet进行微调的效果。
     
     图7：基于放大后的DeepFool对抗扰动进行的微调。
     
     图8：从“1”到“7”：原始图像被分类为“1”，以及使用不同α值时经DeepFool算法扰动后被分类为“7”的图像。
   • 准确率变化：在微调实验中，DeepFool微调能提高网络准确率，而快速梯度符号法微调则导致所有实验中的测试准确率下降。这表明快速梯度符号法输出的过度扰动图像与测试数据分布差异大，起到了非代表性的正则化作用，影响了模型性能，类似几何数据增强中过度变换样本的反作用效果。
     
     表3：在对抗样本上进行微调（五个训练轮次后）后网络的测试误差。每一列对应一种不同类型的增强扰动。
5. 正确评估鲁棒性的重要性：以NIN分类器在快速梯度符号法对抗样本上的微调实验为例，使用不准确的方法（快速梯度符号法）评估对抗鲁棒性会得出错误结论。该方法会夸大训练对对抗样本的影响，且对网络在第一个额外训练轮次中鲁棒性的损失不敏感，突出了使用准确方法评估分类器鲁棒性的关键意义。
   
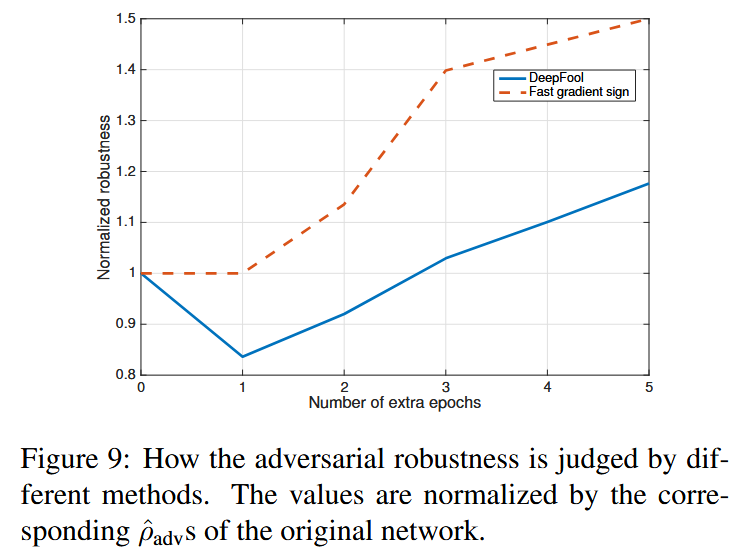
   图9：不同方法是如何判断对抗鲁棒性的。这些数值均通过原始网络相应的 ${\hat{\rho }}_{adv}$ 值进行了归一化处理。

结论-Conclusion

该部分总结了DeepFool算法的核心要点、优势以及应用价值，具体内容如下：

1. 算法核心：提出DeepFool算法，该算法基于对分类器的迭代线性化，生成足以改变分类标签的最小扰动，以此来计算能欺骗当前先进分类器的对抗样本。
2. 算法优势：通过在三个数据集和八个分类器上进行大量实验，充分验证了DeepFool算法相较于当前计算对抗扰动的其他先进方法具有显著优势。它能够更准确地估计对抗扰动，同时计算效率高，在计算对抗扰动任务上表现更优。
3. 应用价值：凭借其对对抗扰动的精确估计，DeepFool算法为评估分类器的鲁棒性提供了一种高效且准确的方式。此外，通过合理的微调，还能提升分类器的性能。因此，该算法可作为可靠工具，用于精确估计最小扰动向量，进而构建更具鲁棒性的分类器，在深度学习模型的安全性和可靠性研究中具有重要的应用价值。