前一段时间一直在学习Linux网络知识,同时准备项目。今天抽出时间就把曾经学过的二叉搜索树这个数据结构拿出来复习一下~
目录
二叉搜索树结点(K模型)
struct BSTreeNode
//key
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};//key
template<class K> //这里实现K模型版本,所以这里先只定义一个模板K
struct BSTreeNode
{
BSTreeNode<K>* _left; //该结点的指向左结点的指针
BSTreeNode<K>* _right; //该节点指向右节点的指针
K _key; //结点中存储的_key值
BSTreeNode(const K& key) //构造函数
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
成员变量定义
typedef BSTreeNode<K> Node;
private:
Node* _root;成员函数
BSTree()
BSTree()
:_root(nullptr)
{}BSTree() //构造函数对指针_root初始化
:_root(nullptr) //注意,结点_root在这里没有调用BSTreeNode构造函数
{}
~BSTree()
~BSTree()
{
Destroy(_root);
}~BSTree() //析构函数,销毁在堆上给结点开辟的空间
{
Destroy(_root); //调用Destroy函数递归释放空间
}
void Destroy(Node* root)
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
//后序遍历递归销毁树
Destroy(root->_left);
Destroy(root->_right);
delete root;
}bool Insert(const K& key)
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //有相同的key时,就不插入数据了
{
return false;
}
}
cur = new Node(key);
//重新判断插入方向
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}bool Find(const K& key)
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}bool Erase(const K& key)
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //找到了,准备删除
{
if (cur->_left == nullptr) //cur的 左为空右为空/左为空右不为空
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else //(parent->_right == cur)
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else //(parent->_left == cur)
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //cur->left != nullptr && cur->_right != nullptr
{
//找cur右子树的最左节点
Node* min = cur->_right;
Node* minParent = cur;//这里给nullptr会出问题
while (min->_left)
{
minParent = min;
min = min->_left;
}
cur->_key = min->_key;//相当于找个结点来替代
if (minParent->_left == min)
{
minParent->_left = min->_right;
}
else
{
minParent->_right = min->_right;
}
delete min;
}
return true;
}
}
return false; //没有找到,cur为空了
}bool EraseR(const K& key)
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else //找到了
{
Node* del = root; //记录要删除的结点
if (root->_left == nullptr) //root是上一个root->_left/root->_right的别名
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else //删除的结点左右都不为空时
{
Node* min = root->_right;
while (min->_left) //找右子树的最左节点
{
min = min->_left;
}
swap(min->_key, root->_key);
//递归到右子树去删除,实际上还是走了上面的条件
//return是递归结束的一个标志
return _EraseR(root->_right, key); //这个地方不return的话下面的delete会走多次!
}
delete del; //走单边树的删除
return true;
}
}Node* FindR(const K& key)
Node* FindR(const K& key) //这里不能直接用_root,在外面穿不进来根节点
{
return _FindR(_root, key);
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (root->_key < key)
{
return _FindR(root->_right, key); //向右递归
}
else if (root->_key > key)
{
return _FindR(root->_left, key); //向左递归
}
else
{
return root;
}
}void InOrder()
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left); //左子树
cout << root->_key << " "; //根
_InOrder(root->_right); //右子树
}bool InsertR(const K& key)
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}K模型完整代码
namespace K
{
//key
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
BSTree()
:_root(nullptr)
{}
~BSTree()
{
Destroy(_root);
}
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //有相同的key时,就不插入数据了
{
return false;
}
}
cur = new Node(key);
//重新判断插入方向
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return true;
}
}
return false;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else //找到了,准备删除
{
if (cur->_left == nullptr) //cur的 左为空右为空/左为空右不为空
{
if (parent == nullptr)
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else //(parent->_right == cur)
{
parent->_right = cur->_right;
}
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr)
{
_root = cur->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else //(parent->_left == cur)
{
parent->_right = cur->_left;
}
}
delete cur;
}
else //cur->left != nullptr && cur->_right != nullptr
{
//找cur右子树的最左节点
Node* min = cur->_right;
Node* minParent = cur;//这里给nullptr会出问题
while (min->_left)
{
minParent = min;
min = min->_left;
}
cur->_key = min->_key;//相当于找个结点来替代
if (minParent->_left == min)
{
minParent->_left = min->_right;
}
else
{
minParent->_right = min->_right;
}
delete min;
}
return true;
}
}
return false; //没有找到,cur为空了
}
Node* FindR(const K& key) //这里不能直接用_root,在外面穿不进来根节点
{
return _FindR(_root, key);
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
bool InsertR(const K& key)
{
return _InsertR(_root, key);
}
bool EraseR(const K& key)
{
return _EraseR(_root, key);
}
private:
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
//后序遍历递归销毁树
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
bool _EraseR(Node*& root, const K& key)
{
if (root == nullptr)
{
return false;
}
if (root->_key < key)
{
return _EraseR(root->_right, key);
}
else if (root->_key > key)
{
return _EraseR(root->_left, key);
}
else //找到了
{
Node* del = root; //记录要删除的结点
if (root->_left == nullptr) //root是上一个root->_left/root->_right的别名
{
root = root->_right;
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else //删除的结点左右都不为空时
{
Node* min = root->_right;
while (min->_left) //找右子树的最左节点
{
min = min->_left;
}
swap(min->_key, root->_key);
//递归到右子树去删除,实际上还是走了上面的条件
//return是递归结束的一个标志
return _EraseR(root->_right, key); //这个地方不return的话下面的delete会走多次!
}
delete del; //走单边树的删除
return true;
}
}
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
{
return _InsertR(root->_right, key);
}
else if (root->_key > key)
{
return _InsertR(root->_left, key);
}
else
{
return false;
}
}
Node* _FindR(Node* root, const K& key)
{
if (root == nullptr)
{
return nullptr;
}
if (root->_key < key)
{
return _FindR(root->_right, key); //向右递归
}
else if (root->_key > key)
{
return _FindR(root->_left, key); //向左递归
}
else
{
return root;
}
}
void _InOrder(Node* root)
{
if (root == nullptr)
{
return;
}
_InOrder(root->_left); //左子树
cout << root->_key << " "; //根
_InOrder(root->_right); //右子树
}
private:
Node* _root;
};
}KV模型完整代码
namespace KV
{
template<class K, class V>
struct BSTreeNode
{
BSTreeNode<K, V>* _left;
BSTreeNode<K, V>* _right;
K _key;
V _value;
BSTreeNode(const K& key, const V& value = V())
:_left(nullptr)
, _right(nullptr)
, _key(key)
, _value(value)
{}
};
template<class K, class V>
class BSTree
{
typedef BSTreeNode<K, V> Node;
public:
BSTree()
:_root(nullptr)
{}
~BSTree()
{
Destroy(_root);
}
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else //又该key的结点,就不插入了
{
return false;
}
}
//找到了地方,开始插入
cur = new Node(key, value);
if (parent->_key > key)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;//用临时变量记录_root,直接用_root迭代的话,_root就被改变了
while (cur)
{
if (cur->_key > key)
{
cur = cur->_left;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else //找到了,准备删除
{
if (cur->_left = nullptr)
{
if (parent == nullptr) //cur为根节点时
{
_root = cur->_right;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else //parent->_right == cur
{
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr)
{
if (parent == nullptr) //cur为根节点时
{
_root = _root->_left;
}
else
{
if (parent->_left == cur)
{
parent->_left = cur->_left;
}
else //parent->_right == cur
{
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else //要删除的结点左右子节点都不为空时
{
Node* minParent = cur;
Node* min = cur->_right;
while (min->_left)
{
minParent = min;
min = min->_left;
}
cur->_key = min->_key;
cur->_value = min->_value;
if (minParent->_left == min)
{
minParent->_left = min->_right;
}
else //minParent->_right == min --->当cur右子树是单树(且全为右子树)的特殊情况
{
minParent->_right = min->_right;
}
delete min;
min = nullptr;
}
return true;
}
}
return false;//没有找到
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void Destroy(Node* root)
{
if (root == nullptr)
{
return;
}
//后序遍历递归销毁树
Destroy(root->_left);
Destroy(root->_right);
delete root;
}
void _InOrder(Node* cur)
{
if (cur == nullptr) //递归一定要有结束条件
{
return;
}
_InOrder(cur->_left);
cout << cur->_key << " : " << cur->_value << endl;
_InOrder(cur->_right);
}
private:
Node* _root;
};
}测试代码
#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
#include"BSTree.h"
using namespace std;
void test_BSTree_K()
{
K::BSTree<int> b;
int arr[] = { 5,3,4,1,7,8,2,6,0,9,5,5 };
for (auto e : arr)
{
b.Insert(e);
}
b.InOrder();
b.Erase(7);
b.InOrder();
b.Erase(5);
b.InOrder();
b.Erase(0);
b.InOrder();
b.Erase(1);
b.InOrder();
for (auto e : arr)
{
b.EraseR(e);
b.InOrder();
}
b.InOrder();
}
void test_BSTree_KV1()
{
//字典KV模型
KV::BSTree<string, string> dict;
dict.Insert("sort", "排序");
dict.Insert("left", "左边、剩余");
dict.Insert("right", "右边、正确");
dict.Insert("search", "搜索");
string str;
while (cin >> str)
{
if (str == "-1")
{
break;
}
KV::BSTreeNode<string, string>* ret = dict.Find(str);
if (ret)
{
cout << "对应的中文翻译:" << ret->_value << endl;
}
else
{
cout << "没有找到" << endl;
}
}
}
void test_BSTree_KV2()
{
//统计水果出现的次数
string arr[] = { "苹果","香蕉","苹果","梨" ,"草莓","西瓜" ,"苹果","草莓" ,"梨","梨" ,"西瓜","香蕉" ,"苹果","西瓜" };
KV::BSTree<string, int> countTree;
//KV::BSTreeNode<string, int> countTree("wmm",1); //调用根节点的构造函数,需要传参
for (const auto& e : arr)
{
KV::BSTreeNode<string, int>* ret = countTree.Find(e);
if (ret == nullptr)
{
countTree.Insert(e, 1); //没有则插入
}
else
{
ret->_value++;
}
}
countTree.InOrder();
}
int main()
{
//test_BSTree_K();
test_BSTree_KV2();
//test_BSTree_KV1();
return 0;
}测试结果:
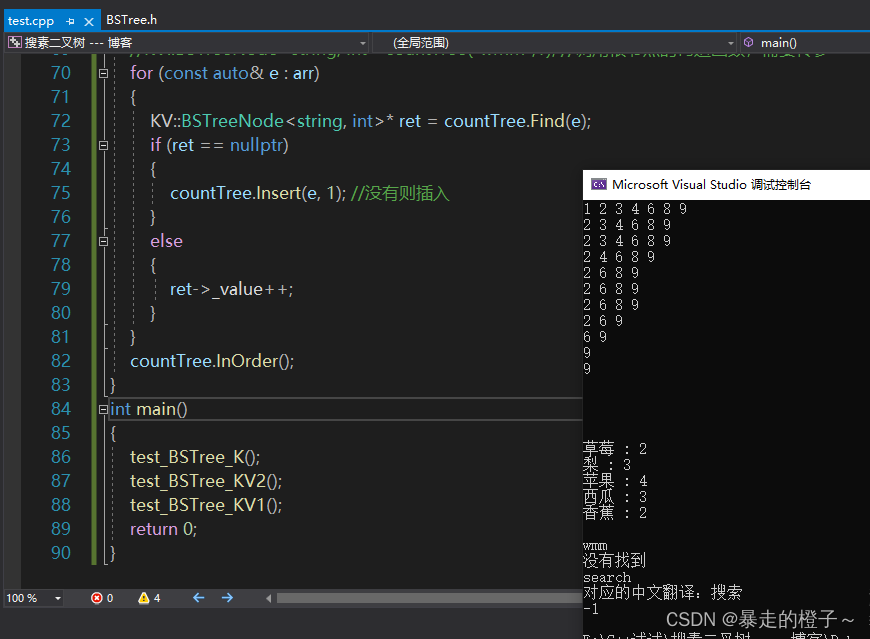





 本文主要复习了二叉搜索树的基本操作,包括插入、查找和删除节点。详细介绍了不同情况下的删除策略,如节点无子节点、只有一个子节点或有两个子节点时的处理。还提供了后序遍历销毁树的实现。通过K模型和KV模型展示了模板类的定义,并给出了测试代码以验证功能的正确性。
本文主要复习了二叉搜索树的基本操作,包括插入、查找和删除节点。详细介绍了不同情况下的删除策略,如节点无子节点、只有一个子节点或有两个子节点时的处理。还提供了后序遍历销毁树的实现。通过K模型和KV模型展示了模板类的定义,并给出了测试代码以验证功能的正确性。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








