学习:
(652条消息) FPGA信号处理系列文章——深入浅出理解多相滤波器_nobel恒等式_十年老鸟的博客-优快云博客
参考上面博客学习了一下原理之后,自己写了一个4倍内插滤波器看效果:
clc
clear
close all
a = 0;
data = [];
for i = 1:10
a = a + 1;
data = [data,a];
end
data_in = upsample(data,4);
% filter_coef = fir1(4*4-1,1/4);
filter_coef = [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16];
div = [];
for i = 1:4
for n = 1:4
div(i,n) = filter_coef(4*(i-1)+n);
end
end
a = filter(filter_coef,1,data_in)
b = filter(div(:,1)',1,data);
c = filter(div(:,2)',1,data);
d = filter(div(:,3)',1,data);
e = filter(div(:,4)',1,data);
see = zeros(5,100);
see(1,1:length(a)) = a;
see(2,1:length(b)) = b;
see(3,1:length(c)) = c;
see(4,1:length(d)) = d;
see(5,1:length(e)) = e;
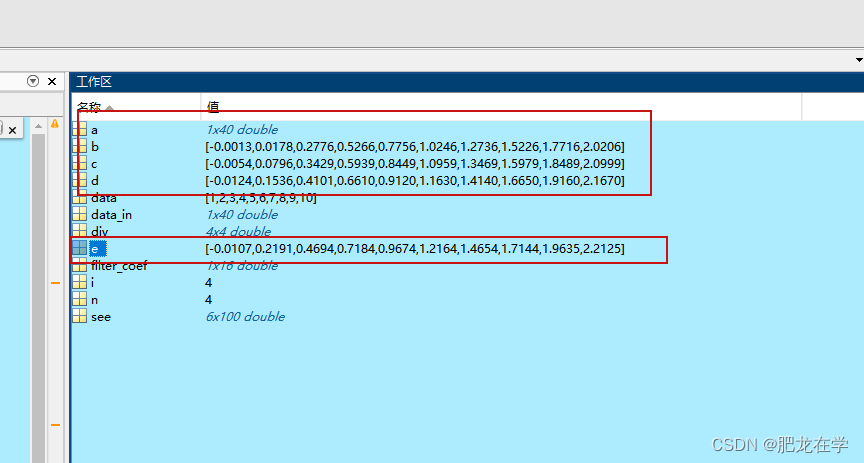
前两行为a,后四行为bcde

可以看到分成4组进行滤波和直接一组进行滤波结果是一样的
只需要在分组滤波之后将数据在拼接起来就ok
理解:
如果不对输入数据进行插值,而是直接将滤波器分组滤波,之后直接将分组滤波后的数据拼接起来的话,相当于间接的对原始数据进行了(组数)倍插值(0),省去了内插0的步骤。
采样率转换:
假如原始采样率为200(fs)M,符号速率为5M(ps),那么此时一个符号的采样点数为200/5 = 40;
如果要实现一个符号4个点
那么只需要对原始数据进行200/4*5(fs/4*ps)=10倍抽取即可




 本文介绍了通过FPGA实现的多相滤波器,特别是4倍内插滤波器的设计过程。作者使用MATLAB演示了如何将滤波器分解为多个部分并分别应用,证明了这种方法等效于直接使用单个滤波器进行4倍内插。此外,还讨论了采样率转换的概念,例如从200Mfs到5Mps的符号速率下,如何通过抽取实现一个符号4个点的目标。
本文介绍了通过FPGA实现的多相滤波器,特别是4倍内插滤波器的设计过程。作者使用MATLAB演示了如何将滤波器分解为多个部分并分别应用,证明了这种方法等效于直接使用单个滤波器进行4倍内插。此外,还讨论了采样率转换的概念,例如从200Mfs到5Mps的符号速率下,如何通过抽取实现一个符号4个点的目标。

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








