蓝桥杯——ALGO-9—— 算法训练摆动序列-优快云博客

本文介绍了一种使用动态规划算法来计算特定条件下摆动序列数量的方法。针对输入的整数k，程序能够找出所有由不大于k的正整数组成且符合摆动序列定义的不同序列的数量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

资源限制：

时间限制：1.0s 内存限制：512.0MB

问题描述：

　　如果一个序列满足下面的性质，我们就将它称为摆动序列：
　　1. 序列中的所有数都是不大于k的正整数；
　　2. 序列中至少有两个数。
　　3. 序列中的数两两不相等；
　　4. 如果第i – 1个数比第i – 2个数大，则第i个数比第i – 2个数小；如果第i – 1个数比第i – 2个数小，则第i个数比第i – 2个数大。
　　比如，当k = 3时，有下面几个这样的序列：
　　1 2
　　1 3
　　2 1
　　2 1 3
　　2 3
　　2 3 1
　　3 1
　　3 2
　　一共有8种，给定k，请求出满足上面要求的序列的个数。

输入格式：

　　输入包含了一个整数k。（k<=20）

输出格式：

　　输出一个整数，表示满足要求的序列个数。

样例输入：

样例输出：

解题思路：

用动态规划解决此问题
设C(i,j)表示当k = i时，用j个数组成的摆动序列有多少种
j = 2即两个数组成时，随便排列组合都是摆动序列，即有C(i , 2) = A(i,2) = i * (i - 1)
动态规划表：

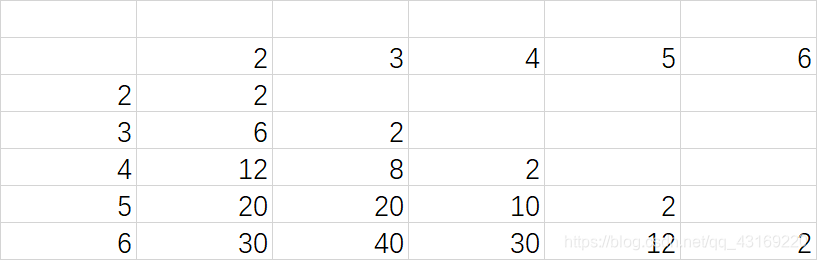
通过此表可得：C(i,j) = C(i - 1，j - 1) + C(i - 1, j)

代码如下：

import java.util.*;
 
public class Main
{
    public static void main(String args[])
    {
        Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		
		int [] [] a=new int[n+1][n+1];
		//两个数无论怎么组合都是摆动序列，所以求A(i,2)
		for (int i = 2; i < a.length; i++) {
			a[i][2]=i*(i-1);
			a[i][i]=2;
		}
		//例如从4，3开始，a[i][j]表示K = i时由j个数组成的摆动序列有多少种
		for (int i = 3; i < a.length; i++) {
			for (int j = 3; j < i; j++) {
				a[i][j]=a[i-1][j-1]+a[i-1][j];
			}
		}
		//将一行的数据加起来
		int sum=0;
		for (int i = 2; i < a[n].length; i++) {
			sum+=a[n][i];
		}
		System.out.println(sum);
    }
}

运行结果如下：