递推练习之费解的开关

费解的开关

题目链接：

费解的开关

思路：

我们要明白一下三个点：

1. 一个方块变化两次后就相当于没变
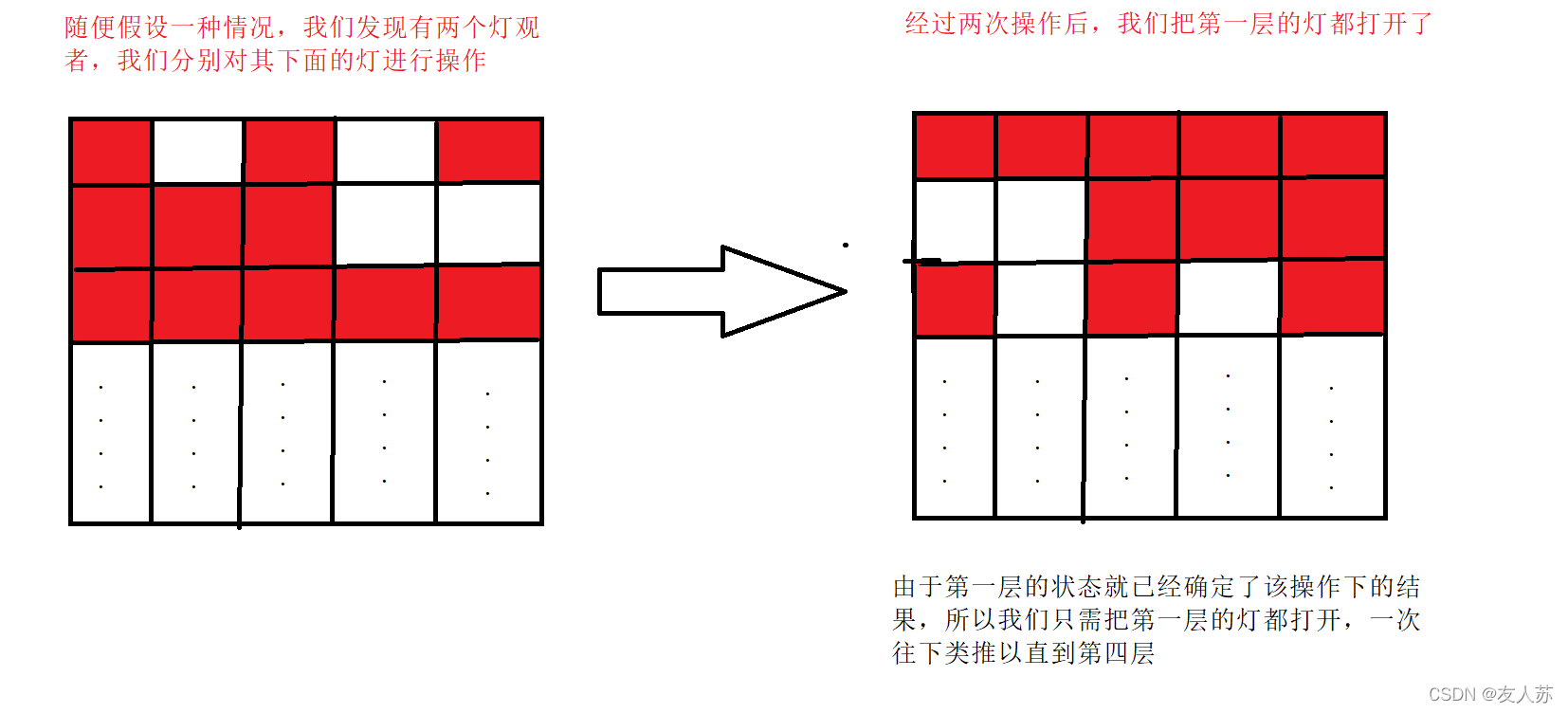
2. 第一层的灯变化后的状态，实际上就决定了整个的结果（重点）
3. 遵循第二点，后面的灯该如何开关，都取决于第一层灯的状态，假设g[0][2] = 0，说明第一层第三个灯是关的，那么我们只能改变g[1][2]，来打开它。

第二个结论我就不证明了，证明起来相当麻烦，用语言难以表达

分析：

根据第二点，我们要明白，既然第一层的变化决定了这组灯能否在规定的条件内全部打开，那么我们只要根据第一层的开关对下面的开关进行操作，遍历所有第一层可能出现的状态，然后我们需要对每一种状态从上到下遍历1到4层，假设哪个灯是关的，那么对其下面的灯进行操作，从而把他打开，遍历结束后，我们知道，前4层的灯都是开的，所以我们只需要查看最后一行有没有关的灯，如果有说明不能达到条件，如果没有，那判断操作数是否在6以内，同时找出最小的操作数。

我们先看看代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int N = 6;
int n;
char g[N][N], backup[N][N];

int dx[5] = {0, 0, 0, 1, -1}, dy[5] = {1, -1, 0, 0, 0};//方向数组，对上下左右的位置进行变换

//变化
void turn(int x, int y){
    for(int i = 0; i < 5; i++){
        int a = x + dx[i], b = y + dy[i];
        if(a < 0 || a >= 5 || b < 0 || b >= 5)continue;
        backup[a][b] ^= 1;
    }
}


int main(){
    int T;
    cin >> T;
    while(T--){
        for(int i = 0; i < 5; i++)
            for(int j = 0; j < 5; j++)
                cin >> g[i][j];
        int res = 10;//res用来存储最小操作数，所以先给他一个较大的值
        
        //模拟所有情况，也就是第一层的状态
        for(int state = 0; state < 32; state++){//为什么要用state遍历32次，请大家看下面的图解
            memcpy(backup, g, sizeof g);
            int step = 0;
            bool dark = false;
            //模拟第一层，对第一层进行操作
            for(int i = 0; i < 5; i++){
                if(state >> i & 1){
                    step++;
                    turn(0, i);
                }
            }
            //根据上面对第一层的操作结果后，开始向下遍历
            for(int i = 0; i < 4; i++){
                for(int j = 0; j < 5; j++){
                    if(backup[i][j] == '0'){
                        step++;
                        turn(i + 1, j);
                    }
                }
            }
            //遍历最后一行，查看是否所有的灯都关闭了
            for(int i = 0; i < 5; i++){
                if(backup[4][i] == '0'){
                    dark = true;
                    break;
                }
            }
            //如果关闭说明成功，step与res比较
            if(!dark)res = min(res, step);
        }
        //规定要在六步以内
        if(res > 6)res = -1;
        cout << res << endl;
    }
    return 0;
}

对于第一层大循环的32次遍历的解释：

首先我们知道，第一层的状态决定了整个的结果，所以我们要对第一层的每种状态进行遍历，而第一层有多少种结果呢，很明显是2的5次方，因为一共有五个灯，而每个灯都有变和不变两种选择，5个灯，那就是2的5次方，也就是32种情况，而我们通过0—31这32个数字分别表示32种情况，大家可以在草稿纸上推算一下0-31的二进制数，每一位表示一个灯，为0说明是关的，为1说明是开的。