刷leetcode——代码随想录（一）

二分查找

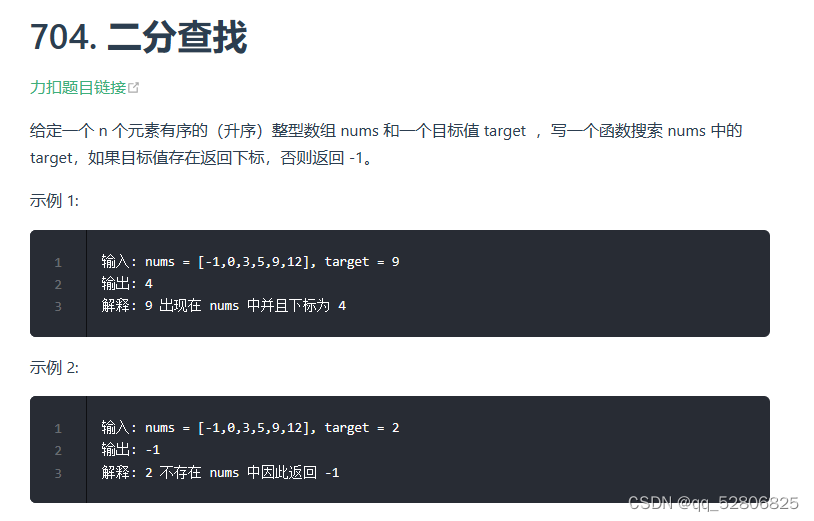
704.二分查找

做题思路 +代码

        由于已经提示二分查找，做这题立马就有思路。本来从题目中有序数组就应该能想到二分查找。设立左边界和右边界，用边界的中间值与目标值做对比。如果中间值小于目标值，则将左边界移到中间值的后一位；如果中间值大于目标值，则将右边界移到中间值的前一位。循环条件为左边界小于等于右边界。

class Solution {
    public int search(int[] nums, int target) {
        int len = nums.length;
        int left = 0, right = len-1;
        while(left <= right){
            int mid = (right - left)/2 + left;
            int num = nums[mid];
            if(num == target){
                return mid;
            }
            else if(num > target){
                right = mid - 1;

            }
            else if(num < target){
                left = mid + 1;
            }
        }
        return -1;

    }
}

35.搜索插入位置

做题思路+代码

        这道题也是简单的二分查找。首先，将目标值与排序数组的左右边界进行对比，如果目标值小于数组最小值，则返回0；如果目标值大于数组最大值，则返回数组长度。接下来，还是设立左边界和右边界，用边界的中间值与目标值做对比。如果中间值小于目标值，则将左边界移到中间值的后一位；如果中间值大于目标值，则将右边界移到中间值的前一位。循环条件为左边界小于等于右边界。最后，循环结束后，如果目标值大于现在的左边界值，则返回左边界+1；如果目标值小于现在的左边界值，则返回左边界。（这个代码用了很多判断，但比较容易理解）

class Solution {
    public int searchInsert(int[] nums, int target) {
        int len = nums.length;
        int left = 0, right = len - 1;
        if(nums[0] >= target){
            return 0;
        }
        if(nums[len-1] < target){
            return len;
        }
        while(left <= right){
            int mid = (right - left) / 2 + left;
            int num = nums[mid];
            if(num == target){
                return mid;
            }
            else if(num < target){
                left = mid + 1;
            }
            else if(num > target){
                right = mid - 1;
            }
        }
        if(target > nums[left]){
            return left + 1;
        }
        else{
            return left;
        }

    }
}

34. 在排序数组中查找元素的第一个和最后一个位置

做题思路+代码

        还是按照二分查找思路在数组中寻找目标值，如果找到目标值则用变量temp记录目标值之一的位置，并且直接退出循环。接下来，对temp左右两边的值进行搜索。（这种做法如果当目标值在数组中有很多时，寻找起始位置时间会很久）

class Solution {
    public int[] searchRange(int[] nums, int target) {
        int left = 0, len =nums.length, right = len - 1;
        int[] nums1 = new int[2];
        nums1[0] = -1; 
        nums1[1] = -1;
        if(len == 0){
            return nums1;
        }
        int temp = -1;
        while(left <= right){
            int mid = (right - left) / 2 + left;
            if(nums[mid] == target){
                temp = mid;
                break;
            }
            else if(nums[mid] < target){
                left = mid + 1;
            }
            else if(nums[mid] > target){
                right = mid - 1;
            }
        }
        if(temp == -1){
            return nums1;
        }
        left = temp;
        right = temp;
        int numleft = temp;
        int numright = temp;
        //System.out.println(temp);

        for(; left >= 0; left--){
            
            if(nums[left] != target){
                break;
            }
            numleft = left;
        }
        //System.out.println(right);
        for(; right < len; right ++){
            if(nums[right] != target){
                break;
            }
            numright = right;

        }
        nums1[0] = numleft;
        nums1[1] = numright;
        return nums1;

    }
}

977.有序数组的平方

做题思路+代码

        这道题可以想到用一个新的数组来保存结果，由于平方后的最大值一定在数组的左边界或者右边界，因此可以从左边界和右边界开始搜寻最大值放入新数组的最末尾，然后不断移动边界寻找剩余数中平方后最大的数值。首先，设立左边界和右边界，以及创建一个返回的新数组用来存储。循环条件为左边界小于等于右边界。然后，比较左边界和右边界的平方值，将其中大的存入新数组的末尾。如果左边大于右边，则将左边界右移；如果右边大于左边，则将右边界左移。直到遍历完全部数组。

class Solution {
    public int[] sortedSquares(int[] nums) {
        int left = 0, right = nums.length - 1;
        int[] result = new int[nums.length];
        int k = nums.length;
        while(left <= right){
            if(nums[left] * nums[left] >= nums[right] * nums[right]){
                result[--k] = nums[left] * nums[left];
                left++;
            }
            else if(nums[left] * nums[left] < nums[right] * nums[right]){
                result[--k] = nums[right] * nums[right];
                right--;
            }
        }
        return result;
    }

}

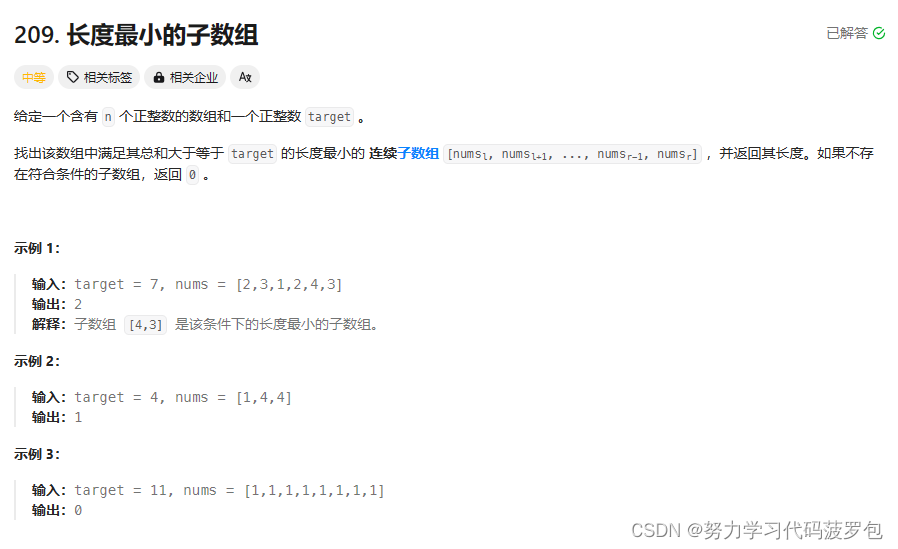
209.长度最小的子数组

做题思路+代码

        设立左右两个指针，固定左指针的位置，移动右指针直到和大于等于目标值。当和大于等于目标值后，最小长度变量保存现在的子数组长度和原长度变量的最小值，再将左指针右移。（我先在最开始将最小长度变量设置为数组长度，但是这样的问题是如果没有符合条件的子数组，最小长度也有数值。因此，我用变量temp来记录是否有过子数组和大于等于目标值的情况）

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int left = 0, right = 0, len = nums.length, num = len;
        int sum = nums[0];
        int temp = 0;
        if(len == 0){
            return 0;
        }
        for(int i = 0; right < len ; i++){
            if(sum < target){
                if(right == len - 1){
                    break;
                }
                right++;
                sum = sum + nums[right];
            }
            else{
                temp = 1;
                num = Math.min(num, right - left + 1);
                sum = sum - nums[left];
                left++;
            }
        }
        if(temp == 0){
            return 0;
        }
        return num;
    }
}

59.螺旋矩阵2

做题思路+代码

        自己开始做的时候毫无思路，看了题解才能做出来。主要思想就是，先设定好矩阵的四条边，然后按照从左到右，从上到下，从右到左，从下到上的顺序来完成。从左到右完成一遍后，上边界加一（向下移），从上到下完成一遍后右边界减一（向左移），从右到左完成一遍后下边界减一（向上移），从下到上完成一遍后左边界加一（向右移）。

class Solution {
    public int[][] generateMatrix(int n) {
        int[][] nums = new int[n][n];
        int l = 0, r = n-1, t = 0, b = n-1;
        int num = 1, tar = n * n;
        while(num <= tar){
            for(int i = l; i <= r; i++){
                nums[t][i] = num++;
            }
            t++;
            for(int i = t; i <= b; i++){
                nums[i][r] = num++;
            }
            r--;
            for(int i = r; i >= l; i--){
                nums[b][i] = num++;
            }
            b--;
            for(int i = b; i >=t; i--){
                nums[i][l] = num++;
            }
            l++;
        }
        return nums;
    }
}

54.螺旋矩阵

做题思路+代码

        思路与上边一样。

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        ArrayList<Integer> list = new ArrayList<Integer>();
        int l = 0, r = n - 1, t = 0, b = m - 1;
        int nums = m * n;
        int k = 0;
        while(list.size() < nums){
            for(int i = l; i <= r; i++){
                list.add(matrix[t][i]);
            }
            t++;
            if(list.size() >= nums){break;}
            for(int i = t; i <= b; i++){
                list.add(matrix[i][r]);
            }
            r--;
            if(list.size() >= nums){break;}
            for(int i = r; i >= l; i--){
                list.add(matrix[b][i]);
            }
            b--;
            if(list.size() >= nums){break;}
            for(int i = b; i >= t; i--){
                list.add(matrix[i][l]);
            }
            l++;
            if(list.size() >= nums){break;}
        }
        return list;

    }
}