力扣刷题Day 79：跳跃游戏 II（45）

1.题目描述

2.思路

方法1（反向贪心）：倒着遍历nums[: n - 1]，找到能够跳到nums[-1]的最小元素索引j，再倒着遍历nums[: j]，找到能够跳到nums[j]的最小元素索引，依次类推，直到最小元素索引为0，得到最小跳跃次数。

方法2（正向贪心）：遍历nums[: n - 1]，找到能够跳到nums[-1]的最小元素索引j，再遍历nums[: j]，找到能够跳到nums[j]的最小元素索引，依次类推，直到最小元素索引为0，得到最小跳跃次数。

方法3（灵茶山艾府佬的建桥思路，真正的贪心，推荐）：

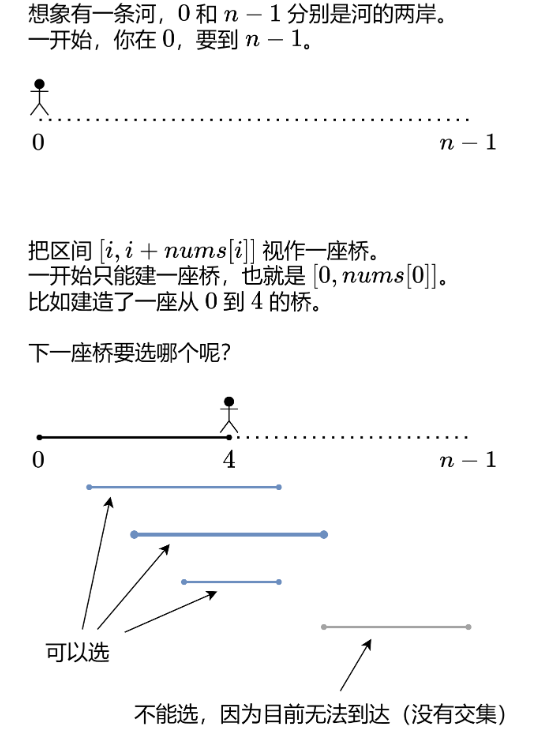
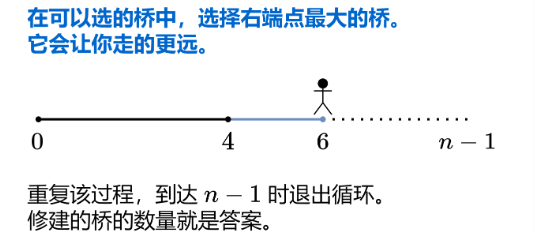
3.代码（Python3）

方法1：

class Solution:
    def jump(self, nums: List[int]) -> int:
        step, n = 0, len(nums) - 1
        while n != 0:
            for i in range(n - 1, -1, -1):
                if i + nums[i] >= n:
                    j = i
            n = j
            step += 1
        return step

方法2：

class Solution:
    def jump(self, nums: List[int]) -> int:
        step, n = 0, len(nums) - 1
        while n != 0:
            for i in range(n):
                if i + nums[i] >= n:
                    n = i
                    break
            step += 1
        return step

方法3：

class Solution:
    def jump(self, nums: List[int]) -> int:
        step = 0
        cur_right = 0 # 已建造的桥的右端点
        next_right = 0 # 下一座桥的最大右端点
        for i in range(len(nums) - 1):
            next_right = max(next_right, i + nums[i]) # 更新下一座桥的最大右端点
            if i == cur_right: # 无路可走必须建桥
                cur_right = next_right # 建桥后最远可到达next_right
                step += 1
        return step

4.执行情况

方法1：

方法2：

方法3：

5.感想

我写的贪心是假贪心吧······