代码思路
1.用一个一维数组array储存每行皇后所在的列,因为棋盘为8*8,所以数组下标index,即代表第index+1个皇后也代表第index+1个位置(第几列).
2.编写一个输出方法,一个判断位置是否符合要求的方法,和一个回溯方法。
3.运用循环int i=0;i<n(n为第n+1个皇后也为第n+1行);i++,当摆放位置与原来皇后摆放的位置为同一列时(array[i]==array[n])或在一条斜线上(Math.abs(array[i]-array[n])==Math.abs(i-n))时,返回false。反之返回true;
4.编写回溯方法,终止条件为n==8(此时,八个皇后都已放入).用循环摆放皇后位置,当符合要求时,再次调用次方法拜访下一个皇后。
代码如下:
public class Queue8APP {
int max=8;
static int count=0;
int[] array=new int[max];
public static void main(String[] args) {
// TODO 自动生成的方法存根
Queue8APP Queue=new Queue8APP();
Queue.Check(0);
System.out.println("总共有"+count+"种方法");
}
private void Check(int n) {//注,每个check都会循环遍历此行的八个位置,eg:当成功后回回溯到第七个继续往后遍历
if(n==max) {//此时八个皇后都已经入位
Print();
System.out.println();
return;
}
for(int i=0;i<max;i++) {
array[n]=i;
if(judge(n)) {//符合要求,摆放下一个皇后
Check(n+1);
}
}
}
private boolean judge(int n) {//判断是否符合要求
for(int i=0;i<n;i++) {
if(array[i]==array[n]||Math.abs(array[i]-array[n])==Math.abs(i-n)) {
return false;
}
}
return true;
}
private void Print() {//遍历数组
count++;
for(int i=0;i<array.length;i++) {
System.out.print(array[i]+" ");
}
}
}
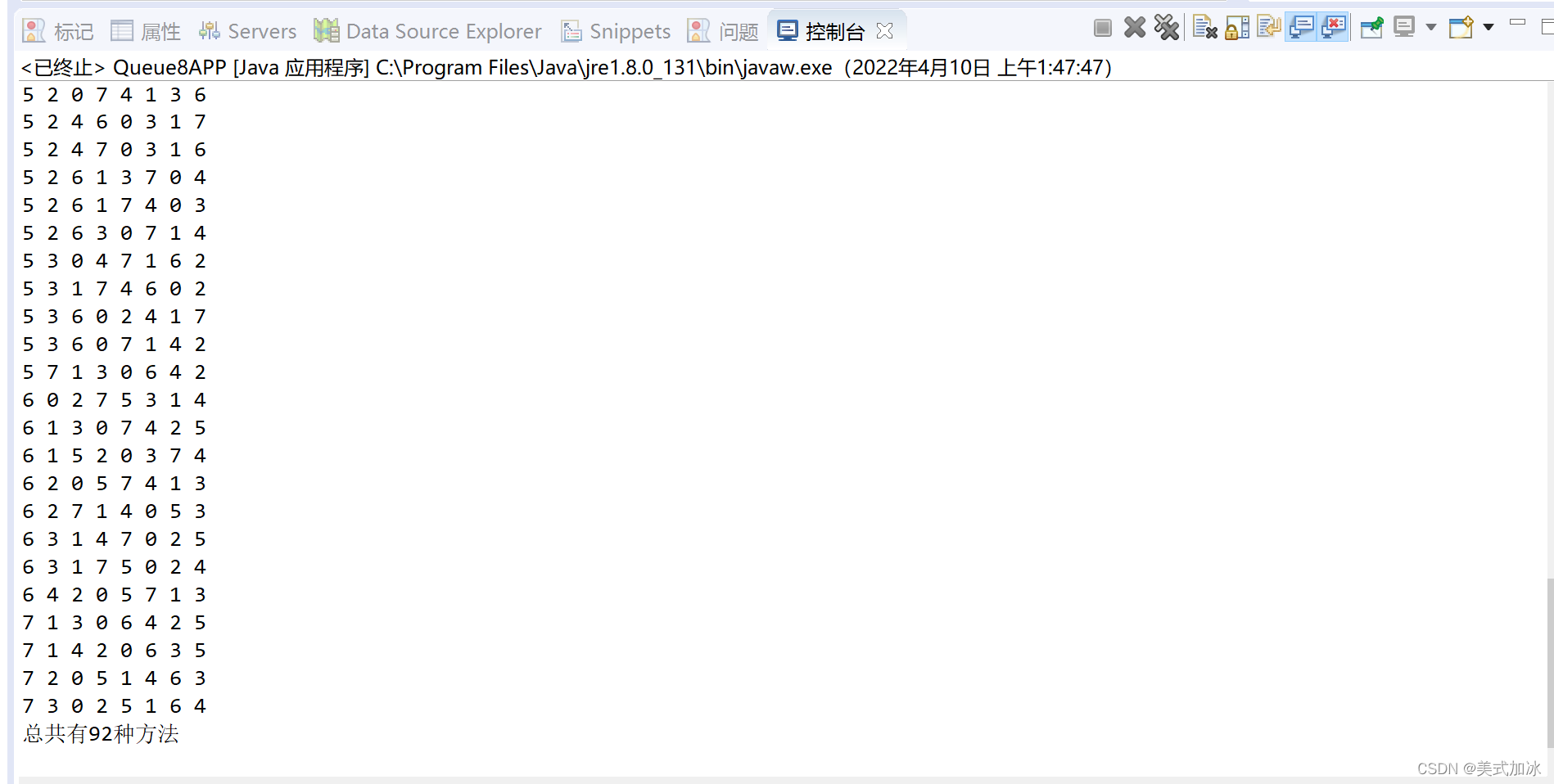








 这篇博客介绍了如何使用回溯算法解决经典的八皇后问题。代码中定义了一个一维数组来存储每一行皇后的列位置,并通过检查当前位置是否与已放置的皇后冲突来判断是否合法。如果合法,则继续放置下一个皇后,否则回溯到上一步。最终,程序会输出所有可能的解决方案数量。
这篇博客介绍了如何使用回溯算法解决经典的八皇后问题。代码中定义了一个一维数组来存储每一行皇后的列位置,并通过检查当前位置是否与已放置的皇后冲突来判断是否合法。如果合法,则继续放置下一个皇后,否则回溯到上一步。最终,程序会输出所有可能的解决方案数量。
















 1256
1256

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








