#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int son[N][26]; // 其中存放的是:子节点对应的idx。其中son数组的第一维是:父节点对应的idx,第第二维计数是:其直接子节点('a' - '0')的值为二维下标。
int cnt [N]; // 以“abc”字符串为例,最后一个字符---‘c’对应的idx作为cnt数组的下标。数组的值是该idx对应的个数。
int idx; // 将该字符串分配的一个树结构中,以下标来记录每一个字符的位置。方便之后的插入和查找。
char str[N];
void insert(char *str)
{
int p = 0;
for (int i = 0; str[i]; i++)
{
int u = str[i] - '0';
if (!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
// 此时的p就是str中最后一个字符对应的trie树的位置idx。
cnt[p]++;
}
int query(char *str)
{
int p = 0;
for (int i = 0; str[i]; i++)
{
int u = str[i] - '0';
if (!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
int n;
scanf("%d", &n);
char op[2];
while (n--)
{
scanf("%s%s", op, str);
if (op[0] == 'I') insert(str);
else printf("%d\n", query(str));
}
return 0;
}
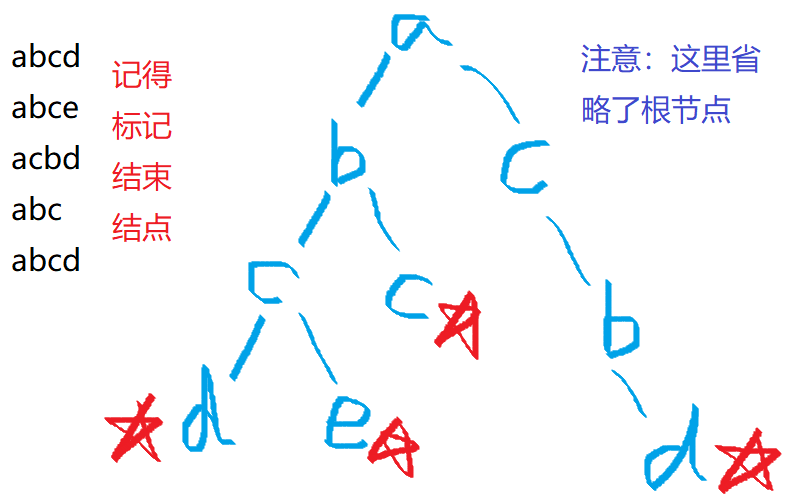
1.关于cnt函数,每次insert都会增加以该字符最后一个字母结尾的数量,查询的时候如图所述就是沿着一条线下来的 ,到达终点节点就可以查找终点节点的数量。
2.关于insert 如果查询到没有这个字符的子节点,就通过idx创造一个新的子节点,并通过son函数记录子节点的id以查询
3关于时间复杂度问题,由于树的节点之间存在着一定关系,搜索时大大减少了搜索时间(也就是具有类似结构的一些数可能有相同的子节点,避免了查询其他节点,故减少了时间复杂度。
习题:最大异或对





 本文介绍了一种使用Trie树实现字符串插入与查询的方法。通过定义son数组记录子节点ID,cnt数组记录以特定节点结尾的字符串数量,实现了高效的数据结构。详细解释了insert与query函数的工作原理及时间复杂度的优势。
本文介绍了一种使用Trie树实现字符串插入与查询的方法。通过定义son数组记录子节点ID,cnt数组记录以特定节点结尾的字符串数量,实现了高效的数据结构。详细解释了insert与query函数的工作原理及时间复杂度的优势。
















 545
545

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








